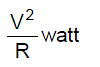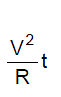Electrical Energy & Power - Notes | Study Physics Class 12 - NEET

Electrical Power

• The energy liberated per second in a device is called its power, the electrical power P delivered by an electrical device is given by
  P = V = VI
• Power consumed by a resistor.
  P = VI = I²R =
• The power P is in watts when I is in amperes, R is in ohms and V is in volts.
• The practical unit of power is 1 kW = 1000 W.
• The formula for power P = I²R = VI =  is true only when all the electrical power is dissipated as heat and not converted into mechanical work, etc. simultaneously.
• If the current enters the higher potential point of the device then electric power is consumed by it (i.e. acts as load). If the current enters the lower potential point then the device supplies power (i.e. acts as source.)

Joule's law of electrical heating

• When an electric current flows through a conductor electrical energy is used in overcoming the resistance of the wire. If the potential difference across a conductor of resistance R is V volt and if a current of I ampere flows the energy expanded in time t seconds is given by
  W = VIt joule = I²Rt joule =  
• The electrical energy so expanded is converted into heat energy and this conversion is called the heating effect of electric current.
• The heat generated in joules when a current of I amperes flows through a resistance of R ohm for t seconds is given by
  
  This relation is known as Joule's law of electrical heating.

Example 1.  If bulb rating is 100 watt and 220 V then determine

(a) Resistance of filament

(b) Current through filament

(c) If bulb operate at 110 volt power supply then find power consume by bulb.

Sol. Bulb rating in 100 W and 220 V bulb means when 220 V potential difference is applied between the two ends then the power consume is 100 W

Here V = 220

P = 100

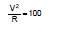
So R = 484 W

Since Resistance depends only on material hence it is constant for bulb

power consumed at 110 V

Therefore, power consumed = 

Example 3. In the following figure, grade the bulb in order of their brightness :

Sol. 

Power = i²R

As current passing through every bulb is same

Therefore, Brightness order is B₃ > B₂ > B₁

Example 4. 

The above configuration shows three identical bulbs, Grade them in order of their brightness.

Sol. B₁ & B₂ withdraw less current as compared to B₃ because in series they give 2R resistance where as R is the resistance due to B₃.

Power = i²R

Therefore, Brightness order : B₃ > B₂ = B₁.

Example 5.

Grade the bulbs in order of their brightness (All bubls are identical)

Sol. 

Therefore, Order of Brightness : B₅ > B₁ = B₂ > B₆ > B₄ = B₃

(B) Maximum power transfer theorem

Let E be emf and r internal resistance of the battery. It is supplying current to an external resistance R

current in circuit I = 

The power absorbed by load resistor R is

P = I²R = 

For maximum power transfer we take the derivative of P w.r.t R, set it equal to zero and solve the equation for R.

Solving for R, we have

(R r)² - R (2) (R r) = 0

(R r) - 2R = 0   

R = r

For a given real battery the load resistance maximizes the power if it is equal to the internal resistance of the battery.

The maximum power transfer theorem in general, holds for any real voltage source. The resistance R may be a single resistor or R may be the equivalent resistance of a collection of resistors.

Instruments

Ammeter

• It is a device used to measure current and its always connected in series with the 'element' through which current is to be measured, e.g., in figure (A) ammeter A₁ will measure the current (I₁) through resistance R₁, A₂ measures current (I₂) through R₂ and R₃ while A, measures current I( I₁ + I₂).

Regarding an ammeter it is worth noting that :

• The reading of an ammeter is always lesser than actual current in the circuit, e.g., true current in the resistance R in the circuit shown in figure (B) is I =
• However, when an ammeter of resistance r is used to measure current as shown in figure (C), the reading will be
  
    
• Smaller the resistance of an ammeter more accurate will be its reading. An ammeter is said to be ideal if its resistance (r) is zero. However, as practically r ¹ 0, ideal ammeter cannot be realised in practice.
• To convert a galvanometer into an ammeter of a certain range say I, a small resistance S (called shunt) is connected in parallel with the galvanometer so that the current passing through the galvanometer of resistance G becomes equal to its full scale deflection value I_g. This is possible only if
  i.e.,          

Example 6. What is the value of shunt which passes 10% of the main current through a galvanometer of 99 ohm?

Sol. As in figure R_gI_g = (I - I_g)S

⇒                    

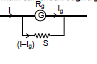
⇒ S = 11 ?

For calculation it is simply a resistance

Resistance of ammeter

for S << R_G                    ⇒           R_A = S

Example 7. Find the current in the circuit also determine percentage error in measuring in current through an ammeter (a) and (b).

Sol. In A 

In B 

Percentage error is =  = 20% Ans.

Here we see that due to ammeter the current has reduced. A good ammeter has very low resistance as compared with other resistors, so that due to its presence in the circuit the current is not affected.

Example 8. Find the reading of ammeter. Is this the current through 6 W ?

Sol. 

Current through battery

So, current through ammeter

No, it is not the current through the 6W resistor.

Note: Ideal ammeter is equivalent to zero resistance wire for calculation potential difference across it is zero.

Voltmeter

It is a device used to measure potential difference and is always put in parallel with the 'circuit element' across which potential difference is to be measured e.g., in Figure (A) voltmeter V₁ will measure potential difference across resistance R₁, V₂ across resistance R₂ and V across (R₁  R₂) with V = V₁  V₂

Regarding a voltmeter it is worth noting that :

(1)The reading of a voltmeter is always lesser than true value, e.g., if a current I is passing through a resistance R [Fig. (B)], the true value V = IR. However, when a voltmeter having resistance r is connected across R, the current through R will become

 and so 

and as voltmeter is connected across R its reading V' is lesser than V.

(2) Greater the resistance of voltmeter, more accurate will be its reading. A voltmeter is said to be ideal if its resistance r is infinite, i.e., it draws no current from the circuit element for its operation. Ideal voltmeter has been realised in practice in the form of potentiometer.

(3) To convert a galvanometer into a voltmeter of certain range say V, a high resistance R is connected in series with the galvanometer so that current passing through the galvanometer of resistance G becomes equal to its full scale deflection value I_g. This is possible only if

V = I_g (G R) i.e.,

Example 9. A voltmeter has a resistance of G ohm and range of V volt. Calculate the resistance to be used in series with it to extend its range to nV volt.

Sol. Full scale current i_g =

to change its range

V₁ = (G R_s) i_g

⇒ nV = (G R_s)