Electromagnetic Induction: Part 2 | Physics Class 12 - NEET PDF Download
What is Inductance?
- Inductance measures how much a coil resists changes in electric current because of the magnetic field it creates. It is the ratio of magnetic flux linkage to current.
- Inductance is expressed in Henrys (H). One Henry means that a change in current of one Ampere per second will create an electromotive force (emf) of one Volt.
- Inductance is a scalar quantity and has dimensions of [ML² T⁻² A⁻²], calculated from the dimensions of flux over the dimensions of current.
- The SI unit of inductance is henry (H), named after Joseph Henry, who independently discovered electromagnetic induction in the USA.
 An Inductor
An Inductor
- When electricity flows through a wire, it generates a magnetic field. If the current changes, this field also changes, producing a type of electric resistance called inductance. An inductor is used to introduce inductance into a circuit.
- There are two types of inductance: self-inductance and mutual inductance.
Self Induction
- Self induction is induction of emf in a coil due to its own current change. Total flux N
 passing through a coil due to its own current is proportional to the current and is given as N
passing through a coil due to its own current is proportional to the current and is given as N  = L i where L is called coefficient of self induction or inductance.
= L i where L is called coefficient of self induction or inductance. - The inductance L is purely a geometrical property i.e., we can tell the inductance value even if a coil is not connected in a circuit. Inductance depends on the shape and size of the loop and the number of turns it has.
- If current in the coil changes by ΔI in a time interval Δt, the average emf induced in the coil is given as, ε =
=
- The instantaneous emf is given as, ε = -
= -
- S.I unit of inductance is wb/amp or Henry (H). It does not depend upon current and is a Scalar Quantity.
- L - self inductance is +ve Quantity.
- It depends on :
(a) Geometry of loop
(b) Medium in which it is kept.
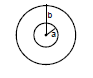
Self Inductance of Solenoid
Let the volume of the solenoid be V, the number of turns per unit length be n. Let a current I be flowing in the solenoid. Magnetic field in the solenoid is given as B = μ0 nl. The magnetic flux through one turn of solenoid f = μ0 n l A.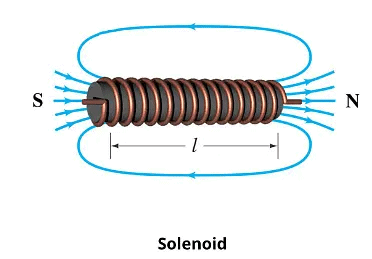
The total magnetic flux through the solenoid = N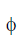
= N μ0 n l A
= μ0 n2 l A l
Therefore, L = μ0 n2 l A = μ0 n2 V
Ф= μ0 n i pr2 (n l)
L = Ф/i = μ0 n2 πr2 l
Inductance per unit volume = μ0 n2
Example 1: The current in a coil of self-inductance L = 2H is increasing according to the law i = 2 sin t2. Find the amount of energy spent during the period when the current changes from 0 to 2 ampere.
Sol. Let the current be 2 amp at t = τ
Then 2 = 2 sin τ2 ⇒ τ =
When the instantaneous current is i, the self induced emf is L 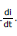 . If the amount of charge that is displaced in time dt is dθ, then the elementary work done
. If the amount of charge that is displaced in time dt is dθ, then the elementary work done
=
W = =
W = =
Let θ = 2t2
Differentiating dθ = 4t dt
Therefore, W =
= L (- cosθ) = - L cos 2t2
W =
= 2 L = 2 × 2 = 4 joule
Inductor
- It is represented by
- Electrical Equivalence of loop
⇒
- If current I through the inductor is increasing the induced emf will oppose the increase in current and hence will be opposite to the current. If current I through the inductor is decreasing the induced emf will oppose the decrease in current and hence will be in the direction of the current.
- Over all result will be VA - L
= VB
Note: If there is a resistance in the inductor (resistance of the coil of inductor) then :
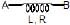
Example 2: A B is a part of circuit. Find the potential difference vA - vB if
(i) current I = 2A and is constant
(ii) current I = 2A and is increasing at the rate of 1 amp/sec.
(iii) current I = 2A and is decreasing at the rate 1 amp/sec.
Sol.
=
Writing KVL from A to B,
VA - 1 - 5 - 2 i = VB
(i) Put I = 2, = 0
VA - 5 - 4 = VB Therefore, VA - VB = 9 volt
(ii) Put I = 2, = 1 ;
VA - 1 - 5 - 4 = VB or VA - VB = 10 V0
(iii) Put I = 2, = - 1
VA + 1 - 5 - 2 × 2 = VB
VA = 8 volt
Energy stored in an Inductor
- If current in an inductor at an instant is i and is increasing at the rate di/dt, the induced emf will oppose the current. Its behaviour is shown in the figure.
- Power consumed by the inductor = i L
- Energy consumed in dt time = i L
dt
- Therefore, total energy consumed as the current increases from 0 to I =
=
⇒ U =
Note: This energy is stored in the magnetic field with energy density
Total energy U =
Example 3: Find out the energy per unit length ratio inside the solid long wire having current density J.
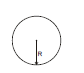
Sol. Take a ring of radius r and thickness dr as an element inside the wire
=
using B =
⇒
⇒
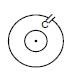
Mutual Inductance
- Consider two coils P and S placed close to each other as shown in the figure. When the current passing through a coil increases or decreases, the magnetic flux linked with the other coil also changes and an induced e.m.f. is developed in it.
- This phenomenon is known as mutual induction. This coil in which current is passed is known as primary and the other in which e.m.f. is developed is called as secondary.
Let the current through the primary coil at any instant be i1. Then the magnetic flux 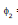 in the secondary at any time will be proportional to i1 i.e.,
in the secondary at any time will be proportional to i1 i.e., 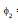 is directly proportional to i1
is directly proportional to i1
Therefore the induced e.m.f. in secondary when i1 changes is given by
i.e.,
=
⇒
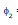 = M i1
= M i1 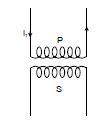
where M is the constant of proportionality and is known as mutual inductance of two coils.
It is defined as the e.m.f. induced in the secondary coil by unit rate of change of current in the primary coil. The unit of mutual inductance is henry (H).
Mutual Inductance of a Pair of Solenoids one Surrounding the Other coil
Figure shows a coil of N2 turns and radius R2 surrounding a long solenoid of length l1, radius R1 and number of turns N1.
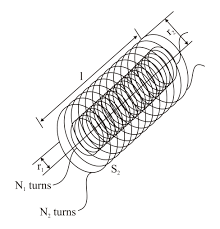
To calculate mutual inductance M between them, let us assume a current i1 through the inner solenoid S1. There is no magnetic field outside the solenoid and the field inside has magnitude,
and is directed parallel to the solenoid's axis. The magnetic flux through the surrounding coil is, therefore,
Now,
Notice that M is independent of the radius R2 of the surrounding coil. This is because solenoid's magnetic field is confined to its interior.
Example 4: Find the mutual inductance of two concentric coils of radii a1 and a2 (a1 << a2) if the planes of coils are same.
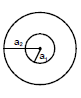
Sol. Let a current I flow in coil of radius a2.
Magnetic field at the centre of coil =
or M i = or
Example 5: Solve the above question, if the planes of coil are perpendicular.
Sol. Let a current i flow in the coil of radius a1. The magnetic field at the centre of this coil will now be parallel to the plane of smaller coil and hence no flux will pass through it, hence M = 0
Example 6: Solve the above problem if the planes of coils make θ angle with each other.
Sol. If i current flows in the larger coil, the magnetic field produced at the centre will be perpendicular to the plane of larger coil.
Now the area vector of smaller coil which is perpendicular to the plane of smaller coil will make an angle θ with the magnetic field.
Thus flux = . πa12 cos θ
or M =
Example 7: Find the mutual inductance between two rectangular loops, shown in figure.
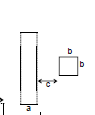
Sol. Consider a segment of width dx at a distance x as shown flux through the regent
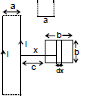
d =
=
⇒  =
=
=
Example 8: Figure shows two concentric coplanar coils with radii a and b (a << b). A current i = 2t flows in the smaller loop. Neglecting self inductance of larger loop
(a) Find the mutual inductance of the two coils
(b) Find the emf induced in the larger coil
(c) If the resistance of the larger loop is R find the current in it as a function of time
Sol. (a) To find mutual inductance, it does not matter in which coil we consider current and in which flux is calculated (Reciprocity theorem) Let current i be flowing in the larger coil. Magnetic field at the centre = .
flux through the smaller coil =
Therefore, M =
(ii) |emf induced in larger coil| =
= =
(iii) current in the larger coil =
Example 9: If the current in the inner loop changes according to i = 2t2 then, find the current in the capacitor as a function of time.
Sol. M =
|emf induced in larger coil| =
e = =
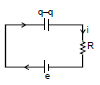
Applying KVL : -
+e - - iR = 0 ⇒
- -iR = 0
differentiate wrt time : -
-
on solving it i =
Series Combination of Inductors
=
Therefore, V = V1 + V2
Leθ = L1 + L2 +.................
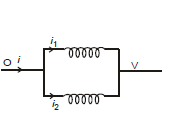
Parallel Combination of Inductors
i = i1 + i2 ⇒
What are Eddy Currents?
- An eddy current is a current set up in a conductor in response to a changing magnetic field. They flow in closed loops in a plane perpendicular to the magnetic field. By Lenz law, the current swirls in such a way as to create a magnetic field opposing the change; for this to occur in a conductor, electrons swirl in a plane perpendicular to the magnetic field.
- Because of the tendency of eddy currents to oppose, eddy currents cause a loss of energy. Eddy currents transform more useful forms of energy, such as kinetic energy, into heat, which isn’t generally useful.
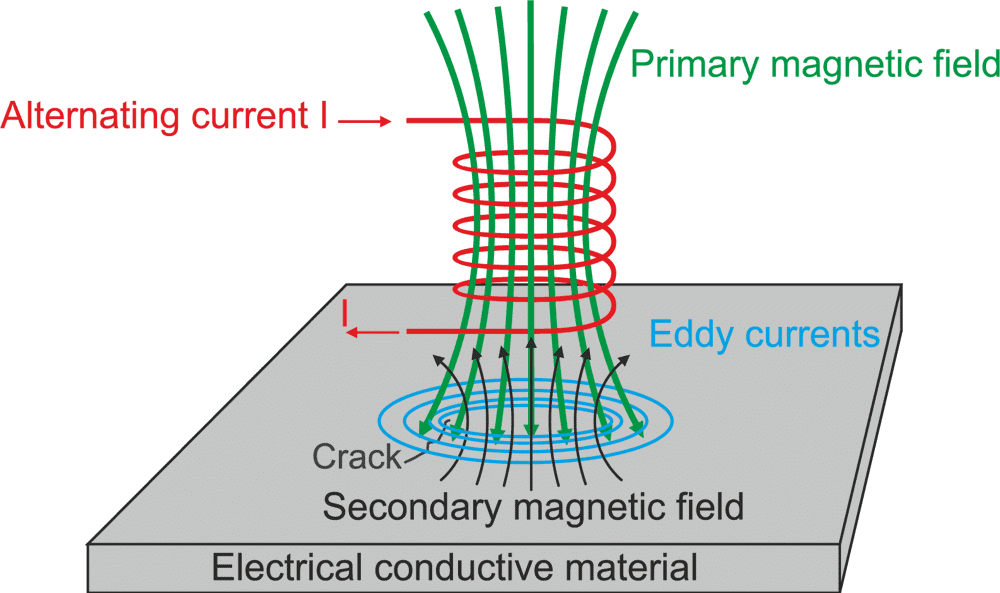 Formation of Eddy Currents
Formation of Eddy Currents
Some Practical Applications
In the Brakes of Trains
When a train brakes, the brakes create a magnetic field that induces eddy currents in the metal wheels. The interaction between this magnetic field and the eddy currents helps to slow down the wheels. As the wheels turn faster, the braking effect increases, which means that as the train reduces speed, the braking force lessens, allowing for a smooth stop.
Electromagnetic Damping
- Used to design deadbeat galvanometers. Usually, the needle oscillates a little about its equilibrium position before it comes to rest. This causes a delay in taking the reading so to avoid this delay, the coil is wound over a non-magnetic metallic frame.
- As the coil is deflected, eddy currents set up in the metallic frame and thus, the needle comes to rest almost instantly.
- Thus, the motion of the “coil is damped”. Certain galvanometers have a fixed core made up of nonmagnetic metallic material. When the coil oscillates, the eddy currents that generate in the core oppose the motion and bring the coil to rest.
Electric Power Meters
The shiny metal disc in the electric power meter rotates due to eddy currents. The magnetic field induces the electric currents in the disc. You can also observe the shiny disc at your house.
 Electric power meters
Electric power meters
Induction Furnace
 Industrial induction furnaceInduction furnaces can achieve temperatures over 1600°C, enough to melt various metals.
Industrial induction furnaceInduction furnaces can achieve temperatures over 1600°C, enough to melt various metals.
- They are mainly used in metal recycling and foundries to melt scrap metal.
- Induction furnaces are also effective for preparing alloys by melting different metals together.
- These furnaces ensure uniform heating and composition during the melting process.
- Known for their high efficiency, induction furnaces produce quality metal with minimal contamination.
- Induction heating operates on the principle of electromagnetic induction, where an alternating current generates a magnetic field that induces currents in the metal charge.
Speedometers
To know the speed of any vehicle, these currents are used. A speedometer consists of a magnet which keeps rotating according to the speed of our vehicle. Eddy currents are been produced in the drum. As the drum turns in the direction of the rotating magnet, the pointer attached to the drum indicates the speed of the vehicle SpeedometerQues: Eddy currents are produced in a metallic conductor when
SpeedometerQues: Eddy currents are produced in a metallic conductor when
(a) The magnetic flux linked with it changes
(b) It is placed in the changing magnetic field
(c) Placed in the magnetic field
(d) Both A and B
Ans: D
Solution: They are produced when the magnetic flux passing through the metal object continuously changes. This may happen due to many reasons.
1. The object is placed in the region with changing magnetic field.
2. The object continuously moves in and out of the magnetic field region.
Power Dissipation of Eddy Currents
Under certain assumptions (uniform material, uniform magnetic field, no skin effect, etc.) the power lost due to eddy currents per unit mass for a thin sheet or wire can be calculated from the following equation:
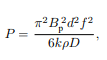 where
where
- P is the power lost per unit mass (W/kg),
- Bp is the peak magnetic field (T),
- d is the thickness of the sheet or diameter of the wire (m),
- f is the frequency (Hz),
- k is a constant equal to 1 for a thin sheet and 2 for a thin wire,
- ρ is the resistivity of the material (Ω m),
- D is the density of the material (kg/m³).
This equation is only relevant under quasi-static conditions, where the frequency does not lead to the skin effect; meaning the electromagnetic wave penetrates the material entirely. Quasi-static conditions indicate that changes in the magnetic field happen slowly enough for the induced currents to adapt without major skin effect losses.
Diffusion Equation
The derivation of a useful equation for modelling the effect of eddy currents in a material starts with the differential, magnetostatic form of Ampère’s Law, providing an expression for the magnetizing field H surrounding a current density J:
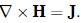
Taking the curl on both sides of this equation and then using a common vector calculus identity for the curl of the curl results in
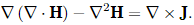
From Gauss’s law for magnetism, ∇ ·H = 0, so

Using Ohm’s law, J = σE, which relates current density J to electric field E in terms of a material’s conductivityσ,and assuming isotropic homogeneous conductivity, the equation can be written as
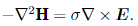
Using the differential form of Faraday’s law, ∇ × E = −∂B/∂t, this gives
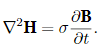
By definition, B = μ0(H+M), where M is the magnetization of the material and μ0 is the vacuum permeability. The diffusion equation therefore is
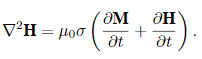
AC Generator
An AC generator is an electric generator that converts mechanical energy into electrical energy in form of alternative emf or alternating current. AC generator works on the principle of ”Electromagnetic Induction”.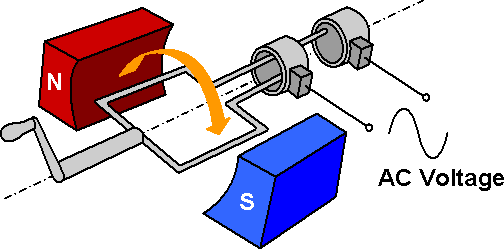
Parts of an AC Generator
- It has two poles, the north and south poles of a magnet, which create a steady magnetic field.
- There is a rectangular coil known as the armature.
- The coils connect to slip rings that are insulated from each other and linked to carbon brushes.
- Each brush connects one end to the slip ring and the other to the circuit.
- The rectangular coils turn around an axis that sits at a right angle to the magnetic field.
- A shaft rotates quickly within the generator.
Working of an AC Generator
- As the armature spins between the magnet's poles, the magnetic flux it experiences changes continuously.
- This variation induces an electromotive force (emf) in the armature, leading to an electric current.
- The current alternates between +ε and -ε, which can be measured by a galvanometer.
Emf Induced in an AC Generator
- If the coil has N turns and an area A, rotating at v revolutions per second in a magnetic field B, the effective area is A cos θ, where θ is the angle between A and B.
- The induced emf can be calculated as e = NBA(2πv)sin(2πvt), assuming the coil is perpendicular to the field at time t = 0 s.
- The direction of the induced emf follows Fleming’s right-hand rule.
Energy Sources for AC Generators
- Mechanical energy for the armature's rotation comes from various sources:
- In hydroelectric generators, falling water is used.
- Thermal generators use steam generated by heating water with coal or other fuels.
- Generators using nuclear fuel are termed nuclear power generators.
- Modern AC generators can produce up to 500 MW of electric power.
Operational Frequency
- The operational frequency in AC generators is usually 50 Hz in India and 60 Hz in countries like the USA.
Solve Questions
Q.1. What replacement is required to convert an AC generator to DC generator
(a) Armature with coil
(b) Concave magnets with horseshoe magnet
(c) Slip rings with split rings
(d) All of the above
Ans: (c)
Solution: In an AC generator, the slip rings connect the moving rotor to the stationary stator. This connection causes the current in the loop to change direction, resulting in alternating current. In contrast, a DC generator uses split rings, which allow current to flow in only one direction, preventing any reversal.
Q.2. What determines the frequency of a.c. produced by a generator?
(a) The number of rotations of coil in one-second
(b) A speed of rotation coil
(c) Both A and B
(d) None of the above
Ans: (c)
Solution: The frequency of alternating current (AC) can be calculated using the formula: f = w/2π, where w represents the angular speed of the coil. In India, the typical frequency of rotation is 50 Hz, while in the USA, it is 60 Hz. The coil's rotation alters the magnetic flux through it, inducing an emf in the coil.
|
74 videos|314 docs|88 tests
|
FAQs on Electromagnetic Induction: Part 2 - Physics Class 12 - NEET
| 1. What is inductance and how is it measured? |  |
| 2. What is self-induction and how does it work? |  |
| 3. How do you calculate the self-inductance of a solenoid? |  |
| 4. What are eddy currents and how do they form? |  |
| 5. What is the difference between series and parallel combinations of inductors? |  |






















