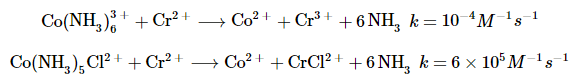Electron Transfer Reactions | Chemistry Optional Notes for UPSC PDF Download
Test Tube Experiments
- Easy chemical or biological reactions performed in test tubes are sometimes called test tube experiments. Solutions in test tubes are mixed at room temperature in air and the mixture is shaken to observe a color change or formation of precipitates and the results of the reactions are speculated on. University professors occasionally attempt these sorts of experiments.
- Although easy, these simple experiments show only the effects of visible light absorption and solubility. However, since even great discoveries can be born from such experiments, they should not be dismissed.
- Henry Taube wrote that he found a hint of the inner-sphere electron transfer mechanism from test tube experiments. He mixed Cr2+(aq) and I2 in a test tube in order to clarify the oxidation of Cr2+(aq) and observed the change of color to the one characteristic of [Cr(H2O)6]3+ via green. The green color is due to [(H2O)5CrI]2+ which is unstable and changes to [Cr(H2O)6]3+ + I-.
- He assumed that this was due to the formation of a Cr-I bond before Cr(II) was oxidized by I2. Subsequently, he performed another test tube experiment using [(NH3)5CoCl]2+ as an oxidant and found that Cr2+(aq) was converted into [Cr(H2O)6]3+ via green [(H2O)5CrCl]2+. This reaction established the inner-sphere electron transfer mechanism in which a Co-Cl-Cr bridge forms between Co3+ and Cr2+ and led to the Nobel Prize in a later year.
Redox reactions
- The oxidation number of the central metal in a transition-metal compound can vary in a few steps from low to high. Namely, the oxidation state of a compound is changeable by redox reactions. As a consequence of this, the bond distance and the bond angle between the metal and coordinating elements, or between metals, change, and at times the whole structure of a complex can be distorted remarkably or the compound may even decompose.
- The reactions of a metal compound with various reducing or oxidizing agents are also very important from the viewpoint of synthetic chemistry. Especially, reduction reactions are used in the preparation of organometallic compounds, such as metal carbonyls or cluster compounds.
- Meanwhile, the study of electron transfer between complexes, especially the redox reactions of transition metal complexes, has developed. Taube won the Nobel Prize (1983) for the study of electron transfer reactions in transition metal complexes, classifying such reactions into two mechanisms.
- The mechanism of electron transfer in which a bridging ligand is shared between two metals is called the inner-sphere mechanism, and the one involving a direct transfer of electrons between two metals without a bridging ligand is called the outer-sphere mechanism.
Inner Sphere Electron Transfer
- In some cases, electron transfers occur much more quickly in the presence of certain ligands. For example, compare the rate constants for the following two electron transfer reactions, involving almost exactly the same complexes:

(Note: aqua ligands are omitted for simplicity. Ions, unless noted otherwise, are aqua complexes.) - Notice two things: first, when there is a chloride ligand involved, the reaction is much faster. Second, after the reaction, the chloride ligand has been transferred to the chromium ion. Possibly, those two events are part of the same phenomenon.
- Similar rate enhancements have been reported for reactions in which other halide ligands are involved in the coordination sphere of one of the metals.
- In the 1960’s, Henry Taube of Stanford University proposed that halides (and other ligands) may promote electron transfer via bridging effects. What he meant was that the chloride ion could use one of its additional lone pairs to bind to the chromium ion. It would then be bound to both metals at the same time, forming a bridge between them. Perhaps the chloride could act as a conduit for electron transfer. The chloride might then remain attached to the chromium, to which it had already formed a bond, leaving the cobalt behind.
- Electron transfers that occur via ligands shared by the two metals undergoing oxidation and reduction are termed "inner sphere" electron transfers. Taube was awarded the Nobel Prize in chemistry in 1983; the award was based on his work on the mechanism of electron transfer reactions.
Solved Example
Example: Take another look at the two electron transfer reactions involving the cobalt and chromium ion, above.
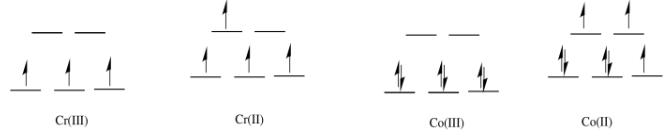
- What geometry is adopted by these complexes?
- Are these species high spin or low spin?
- Draw d orbital splitting diagrams for each complex.
- Explain why electron transfer is accompanied by loss of the ammonia ligands from the cobalt complex.
- The chloride is lost from the cobalt complex after electron transfer. Why does it remain on the chromium?
Ans:
- octahedral
- In the first row, 2+ complexes are almost always high spin. However, 3+ complexes are sometimes low spin.

- The Co(II) complex is high spin and labile. The ligands are easily replaced by water.
- The Cr(III) complex is only d3; it is inert.
Other ligands can be involved in inner sphere electron transfers. These ligands include carboxylates, oxalate, azide, thiocyanate, and pyrazine ligands. All of these ligands have additional lone pairs with which to bind a second metal ion.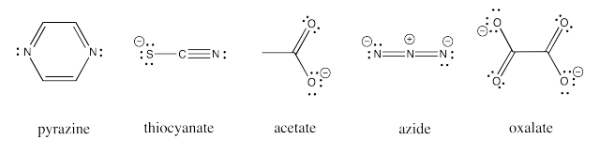
Solved Examples
Example 1: Draw an example of each of the ligands listed above bridging between a cobalt(III) and chromium(II) aqua complex.
Ans: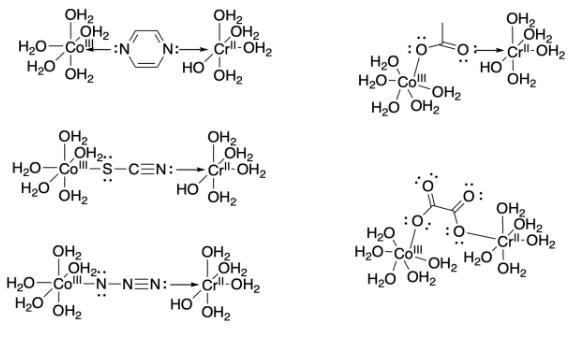
Example 2: Explain, with structures and d orbital splitting diagrams, how the products are formed in the following reaction, in aqueous solution.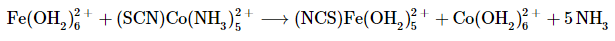
Ans: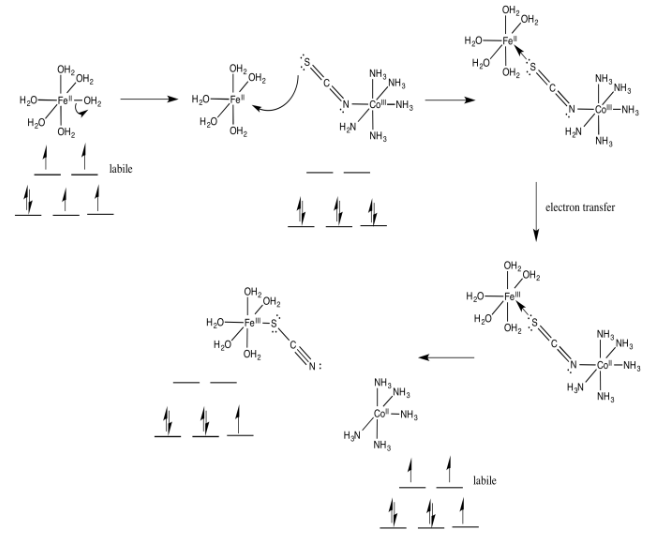
How does the electron travel over the bridge?
- Once the bridge is in place, the electron transfer may take place via either of two mechanisms. Suppose the bridging ligand is a chloride. The first step might actually involve an electron transfer from chlorine to the metal; that is, the chloride could donate one electron from one of its idle lone pairs. This electron could subsequently be replaced by an electron transfer from metal to chlorine.

- Sometimes, we talk about the place where an electron used to be, describing it as a "hole". In this mechanism, the electron donated from the bridging chloride ligand leaves behind a hole. The hole is then filled with an electron donated from the other metal.
- Alternatively, an electron might first be transferred from metal to chlorine, which subsequently passes an electron along to the other metal. In the case of chlorine, this idea may be unsatisfactory, because chlorine already has a full octet. Nevertheless, some of the other bridging ligands may have low-lying unoccupied molecular orbitals that could be populated by this extra electron, temporarily.

Solved Examples
Example 1: For the iron / cobalt electron transfer in problem Exercise 10.5.3 (RO9.3.), show
(a) an electron transfer mechanism via a hole migration along the bridge
(b) an electron transfer mechanism via an electron migration along the bridge
Ans: (a)
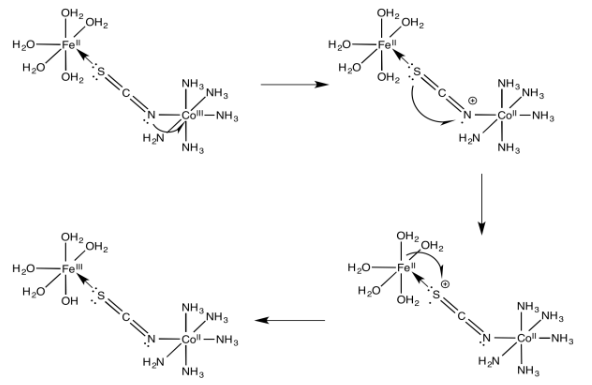
(b)
Example 2: Outer sphere electron transfer rates depend on the free energy change of the reaction (ΔG°) and the distance between oxidant and reductant (d) according to the relation
Rate constant 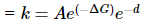
(a) What happens to the rate of the reaction as distance increases between reactants?
One potential problem in measuring rates of intramolecular electron transfer (i.e. within a molecule) is competition from intermolecular electron transfer (between molecules).
(b) What would you do in the flash photolysis experiment above to discourage intermolecular electron transfer?
(c) How could you confirm whether you were successful in discouraging intermolecular reaction?
Ans: (a) The rate decreases exponentially as distance increases.
(b) You might keep the concentration low in order to increase the distance between molecules, reducing the likely hood of an outer-sphere electron transfer.
(c) If you ran the experiment at a series of dilutions, intramolecular electron transfer would be unaffected but outer sphere electron transfer would not. If the rates were the same across a number of different concentrations, the reaction would probably be intramolecular.
Outer Sphere Electron Transfer
- Without a bridging ligand, how does an electron get from one metal to another? This might be a more difficult task than it seems. In biochemistry, an electron may need to be transferred a considerable distance. Often, when the transfer occurs between two metals, the metal ions may be constrained in particular binding sites within a protein, or even in two different proteins.

- That means the electron must travel through space to reach its destination. Its ability to do so is generally limited to just a few Angstroms (remember, an Angstrom is roughly the distance of a bond). Still, it can react with something a few bond lengths away. Most things need to actually bump into a partner before they can react with it.
- This long distance hop is called an outer sphere electron transfer. The two metals react without ever contacting each other, without getting into each others' coordination spheres. Of course, there are limitations to the distance involved, and the further away the metals, the less likely the reaction. But an outer sphere electron transfer seems a little magical.
Barrier to Reaction: A Qualitative Picture of Marcus Theory
So, what holds the electron back? What is the barrier to the reaction? Rudy Marcus at Caltech has developed a mathematical approach to understanding the kinetics of electron transfer, in work he did beginning in the late 1950's. We will take a very qualitative look at some of the ideas in what is referred to as "Marcus Theory". An electron is small and very fast. All those big, heavy atoms involved in the picture are lumbering and slow. The barrier to the reaction has little to do with the electron's ability to whiz around, although even that is limited by distance. Instead, it has everything to do with all of those things that are barely moving compared to the electron.
Imagine an iron(II) ion is passing an electron to an iron(III) ion. After the electron transfer, they have switched identities; the first has become an iron(III) and the second has become an iron(II) ion.
Nothing could be simpler. The trouble is, there are big differences between an iron(II) ion and an iron(III) ion. For example, in a coordination complex, they have very different bond distances. Why is that a problem? Because when the electron hops, the two iron atoms find themselves in sub-optimal coordination environments.
Solved Examples
Example 1: Suppose an electron is transferred from an Fe(II) to a Cu(II) ion. Describe how the bond lengths might change in each case, and why. Don't worry about what the specific ligands are.
Ans: The bonds to iron would contract because the increased charge on the iron would attract the ligand donor electrons more strongly. The bonds to copper would lengthen because of the lower charge on the copper.
Example 2: The optimum O-C-O bond angle in a carbon dioxide molecule is 180 °. Draw a graph of what happens to internal energy when this bond angle varies between 170 ° and 190 °. Don't worry about quantitative labels on the energy axis.
Ans:
The barrier to electron transfer has to do with reorganizations of all those big atoms before the electron makes the jump. In terms of the coordination sphere, those reorganizations involve bond vibrations, and bond vibrations cost energy. Outside the coordination sphere, solvent molecules have to reorganize, too. Remember, ion stability is highly influenced by the surrounding medium.
Solved Example
Example: Draw a Fe(II) ion and a Cu(II) ion with three water molecules located somewhere in between them. Don't worry about the ligands on the iron or copper. Show how the water molecules might change position or orientation if an electron is transferred from iron to copper.
Ans: The water molecules may pivot toward the more highly charged Fe(III), or they may shift closer to it because of the attraction between the ion and the dipole of the water molecule.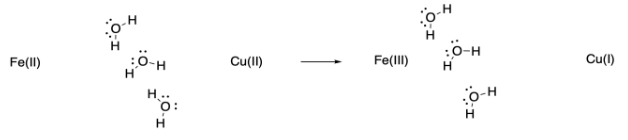 Keep in mind that such adjustments would happen in non-polar solvents, too, although they would involve weaker IMFs such as ion - induced dipole interactions.
Keep in mind that such adjustments would happen in non-polar solvents, too, although they would involve weaker IMFs such as ion - induced dipole interactions.
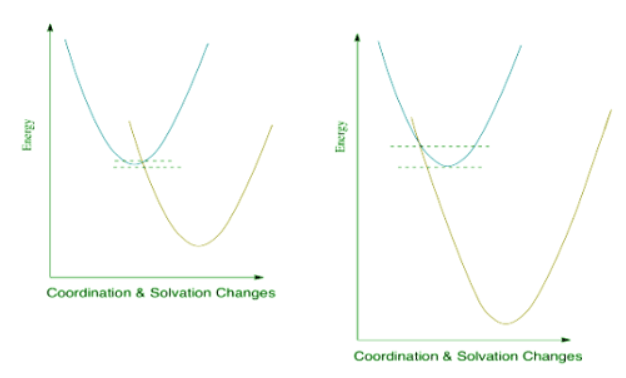
Thus, the energetic changes needed before electron transfer can occur involve a variety of changes, including bond lengths of several ligands, bond angles, solvent molecules, and so on. The whole system, involving both metals, has some optimum set of positions of minimum energy. Any deviations from those positions requires added energy. In the following energy diagram, the x axis no longer defines one particular parameter. Now it lumps all changes in the system onto one axis. This picture is a little more abstract than when we are just looking at one bond length or one bond angle, but the concept is similar: there is an optimum set of positions for the atoms in this system, and it would require an input of energy in order to move any of them move away from their optimum position.
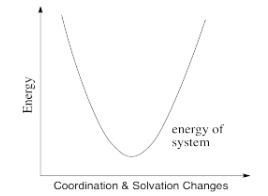
It is thought that these kinds of reorganizations -- involving solvent molecules, bond lengths, coordination geometry and so on -- actually occur prior to electron transfer. They happen via random motions of the molecules involved. However, once they have happened, there is nothing to hold the electron back. Its motion is so rapid that it can immediately find itself on the other atom before anything has a chance to move again.
Consequently, the barrier to electron transfer is just the amount of energy needed for all of those heavy atoms to get to some set of coordinates that would be accessible in the first state, before the electron is transferred, but that would also be accessible in the second state, after the electron is transfered.
Solved Example
Example: Describe some of the changes that contribute to the barrier to electron transfer in the following case.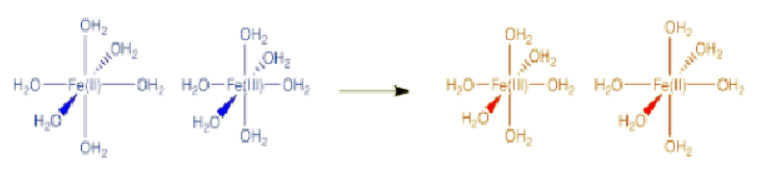 Ans: The reactants and products are very similar in this case. However, the Fe(III) complex has shorter bonds than the Fe(II) complex because of greater electrostatic interaction between the metal ion and the ligands. These changes in bond length needed in order to get ready to change from Fe(III) to Fe(II) (or the reverse) pose a major barrier to the reaction.
Ans: The reactants and products are very similar in this case. However, the Fe(III) complex has shorter bonds than the Fe(II) complex because of greater electrostatic interaction between the metal ion and the ligands. These changes in bond length needed in order to get ready to change from Fe(III) to Fe(II) (or the reverse) pose a major barrier to the reaction.
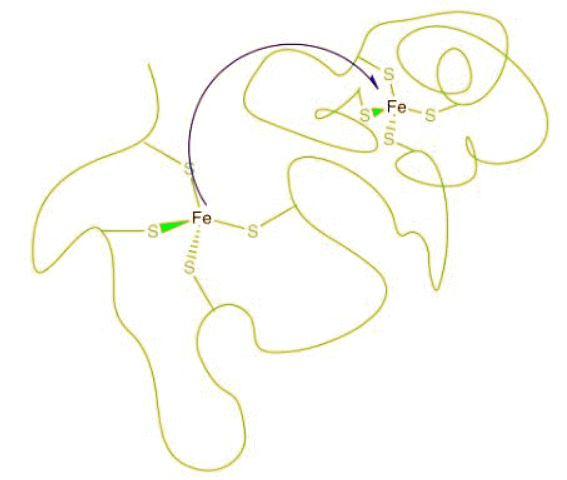
In the drawing below, an electron is transferred from one metal to another metal of the same kind, so the two are just switching oxidation states. For example, it could be an iron(II) and an iron(III), as pictured in the problem above. In the blue state, one iron has the extra electron, and in the red state it is the other iron that has the extra electron. The energy of the two states are the same, and the reduction potential involved in this transfer is zero. However, there would be some atomic reorganizations needed to get the coordination and solvation environments adjusted to the electron transfer. The ligand atoms and solvent molecules have shifted in the change from one state to another, and so our energy surfaces have shifted along the x axis to reflect that reorganization. That example isn't very interesting, because we don't form anything new on the product side. Instead, let's picture an electron transfer from one metal to a very different one. For example, maybe the electron is transferred from cytochrome c to the "copper A" center in cytochrome c oxidase, an important protein involved in respiratory electron transfer.
That example isn't very interesting, because we don't form anything new on the product side. Instead, let's picture an electron transfer from one metal to a very different one. For example, maybe the electron is transferred from cytochrome c to the "copper A" center in cytochrome c oxidase, an important protein involved in respiratory electron transfer.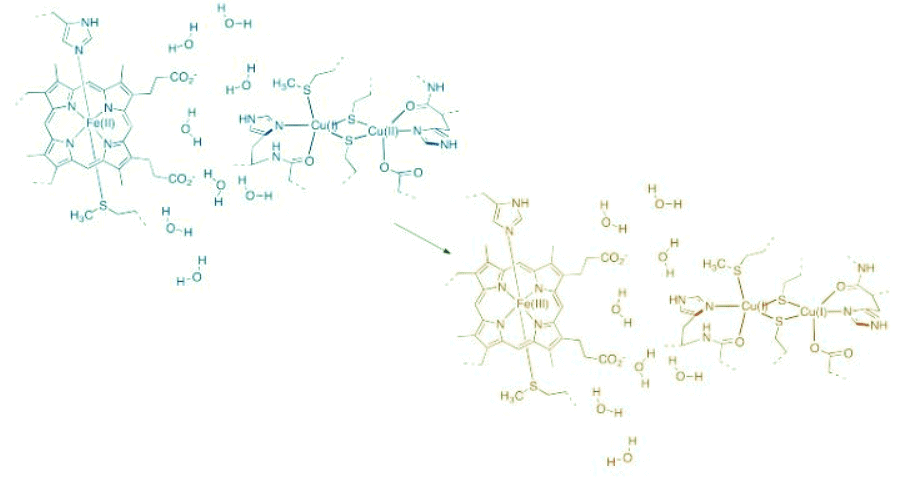
Solved Example
Example: In the drawing above, some water molecules are included between the two metal centres.
- Explain what happens to the water molecules in order to allow electron transfer to occur, and why.
- Suppose there were a different solvent, other than water, between the complexes. How might that affect the barrier to the reaction?
Ans:
- The drawing is an oversimplification, but in general the water molecules are shown reorienting after the electron transfer because of ion-dipole interactions. In this case, the waters are shown orienting to present their negative ends to the more positive iron atom after the electron transfer. In reality, in a protein there are lots of other charges (including charges on the ligand) that may take part in additional ion-dipole interactions.
- Because electron transfer is so fast, atomic and molecular reorganisations are actually thought to happen before the electron transfer. The water molecules would happen to shift into a position that would provide the greatest possible stabilisation for the ions and then the electron would be transferred. A less polar solvent than water would be less able to stabilize ions and the electron would be slower to transfer as a result. In addition, a less polar solvent than water would be a poor medium to transmit an electron, which is charged and therefore stabilized by interactions with polar solvents.
The energy diagram for the case involving two different metals is very similar, except that now there is a difference in energy between the two states. The reduction potential is no longer zero. We'll assume the reduction potential is positive, and so the free energy change is negative. Energy goes down upon electron transfer.
Compare this picture to the one for the degenerate case, when the electron is just transferred to a new metal of the same type. A positive reduction potential (or a negative free energy change) has the effect of sliding the energy surface for the red state downwards. As a result, the intersection point between the two surfaces also slides downwards. Since that is the point at which the electron can slide from one state to the other, the barrier to the reaction decreases.
What would happen if the reduction potential were even more positive? Let's see in the picture below.
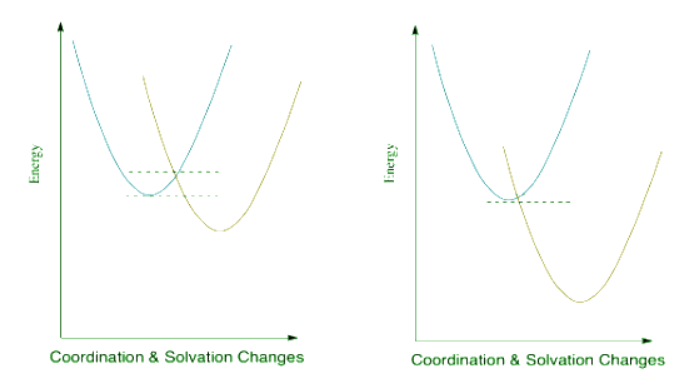
The trend continues. According to this interpretation of the kinetics of electron transfer, the more exothermic the reaction, the lower its barrier will be. It isn't always the case that kinetics tracks along with thermodynamics, but this might be one of them.
But is all of this really true? We should take a look at some experimental data and see whether it truly works this way.
 As the reduction potential becomes more positive, free energy gets more negative, and the rate of the reaction dramatically increases. So far, Marcus theory seems to get things right.
As the reduction potential becomes more positive, free energy gets more negative, and the rate of the reaction dramatically increases. So far, Marcus theory seems to get things right.
Solved Example
Example: (a) Plot the data in the above table.
(b) How would you describe the relationship? Is it linear? Is it exponential? Is it direct? Is it inverse?
(c) Plot rate constant versus free energy change. How does this graph compare to the first one?
Ans: (a) Here is a plot of the data.
(b) It doesn't look linear. If we plot the y axis on a log scale, things become a little more linear.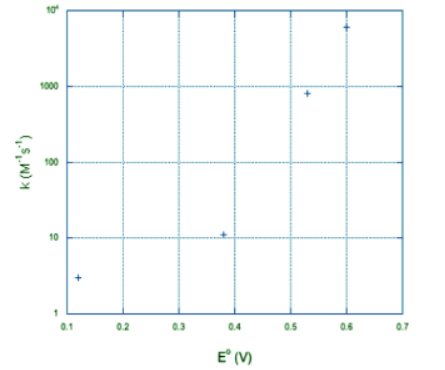 It looks closer to a logarithmic relationship than a linear one.
It looks closer to a logarithmic relationship than a linear one.
(c) Assuming one electron transfer: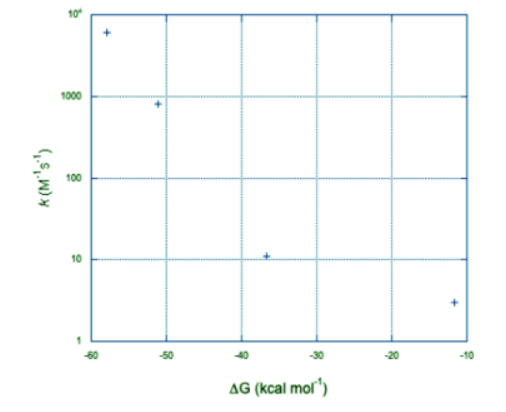 The graph takes the same form but in the opposite direction along the x axis.
The graph takes the same form but in the opposite direction along the x axis.
Marcus Inverted Region
- When you look a little closer at Marcus theory, though, things get a little strange. Suppose we make one more change and see what happens when the reduction potential becomes even more positive.

- So, if Marcus is correct, at some point as the reduction potential continues to get more positive, reactions start to slow down again. They don't just reach a maximum rate and hold steady at that plateau; the barrier gets higher and higher and the reactions get slower and slower. If you feel a little skeptical about that, you're in good company.
- Marcus always maintained that this phenomenon was a valid aspect of the theory, and not just some aberration that should be ignored. The fact that nobody had ever actually observed such a trend didn't bother him. The reason we didn't see this kind of thing, he said, was that we just hadn't developed technology that was good enough to measure these kind of rates accurately.
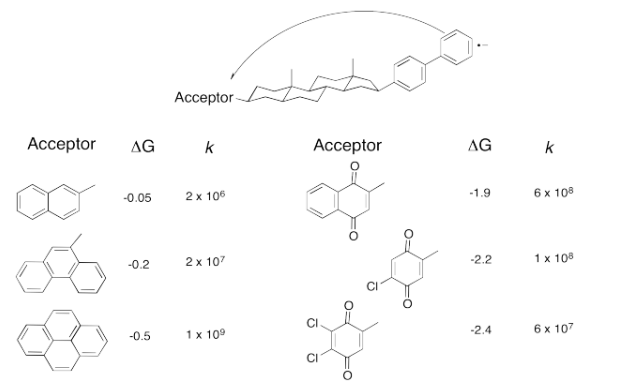
- But technology did catch up. Just take a look at the following data (from Miller, J. Am.Chem. Soc. 1984, 3047).

- Don't worry that there are no metals involved anymore. An electron transfer is an electron transfer. Here, an electron is sent from the aromatic substructure on the right to the substructure on the left. By varying the part on the left, we can adjust the reduction potential (or the free energy change, as reported here.
Solved Examples
Example 1: Take a look at the donor/acceptor molecule used in Williams' study, above.
(a) Why do you suppose the free energy change is pretty small for the first three compounds in the table?
(b) Why does the free energy change continue to get bigger over the last three compounds in the table?
Ans: The acceptor compound becomes an anion when it accepts an electron. The first three compounds do not appear to be strongly electrophilic; they can accept electrons simply because of resonance stability of the resulting anion. The last three have electron withdrawing groups (chlorines and oxygens) that would stabilize the anion even further.
Example 2: (a) Plot the data in the above table.
(b) How would you describe the relationship?
Ans: (a) 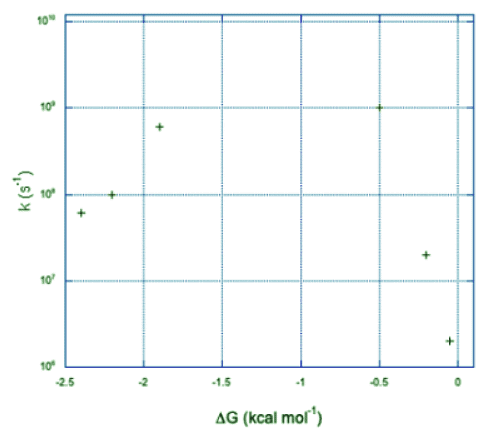 (b) We can see two sides of an inverted curve. The reaction gets much faster as the free energy becomes more negative, but at some point the rate begins to decrease again.
(b) We can see two sides of an inverted curve. The reaction gets much faster as the free energy becomes more negative, but at some point the rate begins to decrease again.
FAQs on Electron Transfer Reactions - Chemistry Optional Notes for UPSC
| 1. How does electron transfer occur in inner sphere experiments? |  |
| 2. What is the process of electron transfer in outer sphere experiments? |  |
| 3. What is the barrier to reaction in Marcus theory? |  |
| 4. What is the Marcus inverted region in electron transfer reactions? |  |
| 5. What are some key concepts of Marcus theory? |  |

|
Explore Courses for UPSC exam
|

|