Equilibria: Types, Relation Between K, Q & G, Applications & Factors Affecting - Notes | Study Chemistry Class 11 - NEET

Homogeneous Equilibrium

We encounter so many reactions around us in our day to day life; the rusting of iron, the burning of paper, the souring of curd, the formation of ozone, etc. Many of these reactions involve the presence of components in different phases, such as solid iron coming in contact with gaseous oxygen to form solid iron oxide, we know as rust. Similarly, gaseous hydrogen combines with gaseous oxygen to form liquid water. Dealing with such reactions is a tedious task. If the components are in the same phase, the interaction of the components can be understood easily, while when the components are in different phases, the interaction gets more complicated.

Introduction to Homogeneous equilibrium
In order to simplify the problems and understand the concept, we divide such reactions into different categories, namely, the homogeneous reactions, where the components involved in the reaction are present in the same phase and the heterogeneous reactions, where the components involved are present in different phases. The methods of dealing with both the reactions are different and so is the determination of the equilibrium state. In this section, we will learn about a homogeneous equilibrium and the calculation of equilibrium constant for a homogeneous reaction.

Equilibrium Constant for Homogeneous Reaction
Let us consider a homogeneous system, given by the following reaction
N2(g) + 3H2(g) ↔ 2NH3(g)
Here, we see that gaseous nitrogen reacts with gaseous hydrogen to form gaseous ammonia. Let us now calculate the equilibrium constant for the above reaction.
In terms of the molar concentration of the components in the reaction, we can write

As we know, for reactions involving gases, we express the equilibrium concentration in terms of the partial pressure.
Using the ideal gas equation,
PV = nRT
Where P is the pressure of the system, V is the volume of the system, n is the number of moles of components present in the system, R is the universal gas constant and T is the temperature of the system.

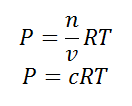
Here, c is the concentration of the system. We can also write it as,
c = P / RT
So equilibrium constant can also be written as,

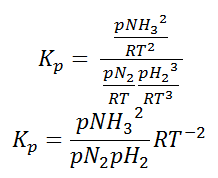
Here, we note that the general expression for Kc and Kp can be written as,
K_P = K_c(RT)^Δn
Where Δn is defined as the number of moles of gaseous products – the number of moles of gaseous reactants.

Heterogeneous Equilibrium

When the state of equilibrium in a system has components in more than one phase it is termed as a heterogeneous equilibrium. For example, if we take a container with ice and water at a temperature that is allowing the existence of both the phases simultaneously, such that, both ice and water are present in a state of equilibrium. This state is termed as heterogeneous equilibrium.
In terms of its equation, this can be written as:
H₂O(s) ↔ H₂O(l)
In another example, we can consider an aqueous solution of a solid such as calcium hydroxide. We notice that the solid calcium hydroxide is in equilibrium with its saturated solution.
Writing the equilibrium constant for heterogeneous reactions is different from that of the homogeneous reactions. For example, consider the thermal dissociation of calcium carbonate into calcium oxide and carbon dioxide. Here, we can see that the equilibrium constant for the dissociation of the reactant into its products is only dependent on the gaseous component, as the solid and the liquid reactants are considered to be constant.
CaCO₃(s) ↔ CaO(s) + CO₂
Here, the components CaCO₃ and CaO are solids, so their molar concentration remains constant throughout the reaction. Therefore, the equilibrium constant can be written as,

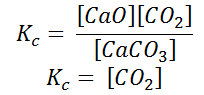
Also, in terms of K_p, we can write
K_p = pCO₂
Where p denotes the partial pressure. In other words, we can state that, at a given temperature, there is a constant concentration or partial pressure of CO₂ in the equilibrium reaction with CaO and CaCO₃.

Effect of Temperature on Equilibrium constant

VAN'T HOFF EQUATION

where K is the equilibrium constant, T is temperature, ΔH is the enthalpy of the reaction and R is the gas constant. It provides means to detemine how the equilibrium constant for a reaction or process will vary with temperature.

Ex. H₂O(l)  H (aq)⁺ + OH^-(aq) , ΔH= 13.7 kcal/mol , K_eq at 25°C =10^-14. Calculate K_eq at 60°C ?

Sol.

K₂= 1.26×10^-12

LeChâtelier principle

If a system at equilibrium is subjected to a change of pressure, temperature, or the number of moles of a substance, there will be a tendency for a net reaction in the direction that tends to reduce the effect of this change.

1. EFFECT OF CHANGE IN CONCENTRATION

The change in concentration can affect gaseous systems or liquid solution systems only. However this does not affect the solid and pure liquid systems since their active masses are always taken as unity. By using le Chatelier's principle, the effect of change in concentration on systems at equilibrium can be explained as follows:

1. When the concentration of reactant(s) is increased, the system tries to reduce their concen tration by favoring the forward reaction.

2. When the concentration of product(s) is increased, the system tries to reduce their concentration by favoring the backward reaction.

3. When the concentration of reactant(s) is decreased, the system tries to increase their concentration by favoring the backward reaction.

4. When the concentration of product(s) is decreased, the system tries to increase their concentration by favoring the forward reaction.

When the concentration of reactants is increased, the number of effective collisions between them increases which in turn increases the rate of forward reaction. Thus the forward reaction is more favored over the backward reaction until the new equilibrium is established. At this new equilibrium, the rates of both forward and backward reactions become equal again and the reaction quotient becomes approximately equal to the equilibrium constant.

Remember that small changes in concentration do not affect the equilibrium constant.

For decomposition reaction , PCl₅(g) PCl₃(g) + Cl₂(g)

Let the concentration of PCl₅ is doubled to disturb the equilibrium. This will change the reaction quotient, Q to:

After disturbing the equilibrium, the value of Q becomes less than KC. In order to restore the Q value to KC, the concentration of PCl₅ must be decreased while the concentrations of PCl₃ and Cl₂ are to be increased. This is achieved by favoring the forward reaction
 

The forward reaction is also favored by removing the products from the reaction mixture (decrease in the concentration of products). Upon removal of products, the rate of forward reaction becomes greater than that of backward reaction momentarily. This will also decrease the reaction quotient. Hence the system tries to reestablish the equilibrium by converting more reactants to products so as to make the rates of both forward and backward reactions become equal again.

For example, in case of the decomposition of PCl₅, if the concentration of Cl₂ is increased by two times at equilibrium, the Q value becomes greater than the KC value.

Hence the system tries to restore the value of Q to KC again. The backward reaction is favored to decrease the concentration of Cl₂. However the concentration of PCl5 also decreases automatically while the concentration of PCl₅ increases while doing so.

2. EFFECT OF CHANGE IN PRESSURE

The change in pressure only affects the equilibrium of systems involving at least one gas. The le Chatelier's principle can be applied to understand the effect of change in pressure on the systems at equilibrium as follows.

1. When the partial pressure of any of the gaseous reactants or of the products is increased, the position of equilibrium is shifted so as to decrease its partial pressure. This is usually achieved by favoring the reaction in which there is decrease in the number of moles of gaseous components.

2. When the partial pressure of any of the gaseous reactants or of the products is decreased, the position of equilibrium is shifted so as to increase its partial pressure. This can be achieved by favoring that reaction in which there is increase in the number of moles of gaseous components.

However, it is not always correct to say that the equilibrium is shifted whenever there is a change in the total pressure of the system. The equilibrium is not always disturbed upon changing the pressure of the entire system. It is only disturbed whenever there is a change in the partial pressure of any or all of the gaseous reactants or products in the equilibrium for which the Dn_g ¹ 0. Where Dn_g = (no. of moles of gaseous products) - (no.of moles of gaseous reactants) Strictly speaking, the equilibrium is only shifted when the ratio of product of partial pressures of products to the product of partial pressures of reactants i.e., the reaction quotient in terms of partial pressures, Qp is disturbed. The position of equilibrium is shifted so as to make Qp become equal to the value of Kp again.

The Q_p can be changed in the following cases:

1. By adding or removing any gaseous reactant or product at constant volume. The effect is same as changing the concentration as explained above.

2. By changing the volume of the system (or in other words by changing the pressure of entire system) at equilibrium for which the Dng ¹ 0. In this case, however, the pressure of the entire system is also changed.

For the decomposition of PCl₅, the Kp can be written as:

For this reaction Dng = (1 + 1)-(1) = 1

Hence for this reaction, if the pressure of the system is increased by 2 times by halving the volume, the reaction quotient, Qp is doubled. In order to restore back the Qp value again to Kp, the denominator value i.e., the partial pressure of PCl₅must be increased. This is only achieved by favoring the forward reaction in which less number of gaseous products are formed. i.e., Two moles of products (PCl₃ and Cl₂) are converted to one mole of reactant (PCl₅)

Therefore we can say, if the pressure of the system is increased, the system tries to decrease it by favoring the reaction in the direction of decreasing the number of moles of gaseous components.

3. Addition of Inert Gas

(A) At constant volume :there is no effect of adding inert gas on the state of equilibrium at constant volume.

(B) At constant pressure : On Adding of inert gas At constant pressure, the reaction proceeds in that direction where the sum of stoichiometric coefficient of gaseous components is greater.

4. EFFECT OF CHANGE IN TEMPERATURE

The effect of temperature can be understood by using le Chatelier's principle as follows:

1. Increase in the temperature of the system favors the endothermic reaction. The increase in temperature increases the amount of heat in the system. Hence it tries to remove the excess of heat by favoring that reaction in which heat is absorbed i.e., the endothermic reation.

2. Decrease in the temperature of the system favors the exothermic reaction. In this case, the temperature is decreased by removing the heat content from the system. Hence the system tries to restore the temperature back by favoring the exothermic reaction i.e., the reaction in which the heat is liberated.

It is very important to note that, during the change in temperature, the system establishes a new equilibrium for which the value of equilibrium constant is different from the original constant i.e., the equilibrium constant depends on the temperature.

EFFECT OF CATALYST

A catalyst has no effect on the position of the equilibrium since it increases not only the rate of forward reaction but also the rate of backward reaction. However it does help the system to reach the equilibrium faster.

Applications of Equilibrium Constant
1. Equilibrium Constant For Predicting the Extent of Reaction
The equilibrium constant (K_c) can be used to predict the extent of a reaction, i.e. the degree of the disappearance of the reactants. The magnitude of the equilibrium constant gives an idea of the relative amount of the reactants and the products.
Case 1: The larger value of the equilibrium constant (>10³) shows that forward reaction is favored i.e. the concentration of products is much larger than that of the reactants at equilibrium.
For Example:

• H₂(g) + Br₂(g) ⇌ 2HBr(g) ⇒ Kc = 5.4 × 10¹⁸
• H₂(g) + Cl₂(g) ⇌ 2HCl(g) ⇒ Kc = 4 × 10³¹
• H₂(g) + 12O₂(g) ⇌ H₂O(g) ⇒ Kc = 2.4 × 10⁴⁷

This shows that at equilibrium, concentration of the products is very high, i.e. reaction go almost to completion.
Case 2: Intermediate value of equilibrium constant (10^-3 to 10³) show that the concentration of the reactants and products are comparable.
For Example:

• Fe₃ (aq) + SCN (aq) ⇌ [Fe(SCN)]₂ (aq) ⇒ K_c = 138 at 298 K
• H₂ (g) + I₂ (g) ⇌ 2HI (g) ⇒ K_c = 57 at 700 K. 

Case 3: Low value of equilibrium constant (<10^-3) shows that backward reaction is favored i.e. concentration of reactants is much larger than that of products i.e. the reaction proceeds to a very small extent in the forward direction.
For Example:

• N₂ (g) + O₂ (g) ⇌ 2NO (g) ⇒ K_c = 4.8 × 10^-31 at 298K
• H₂O (g) ⇌ H₂ (g) + (1/2) O₂ (g) ⇒ K_c = 4.1 × 10^-48 

2. Equilibrium Constant for Predicting the Direction of a Reaction
The equilibrium constant can be used to predict the direction of the reaction. We need a term, reaction quotient (Qc expressed in terms of concentrations or Qp in terms of partial pressures) similar to the equilibrium constant except that the conditions are not at equilibrium.
For a balanced reaction, aA + bB ⇌ cC + dD
Reaction quotient (Qc or Qp) is given as:
Q_c = [C]^c[D]^d / [A]^a[B]^b
Q_p = p^cC × p^dD / p^aA × p^bB
Comparison with Kc and the direction of Reaction:

• If Q = K_c, the reaction is in equilibrium [Where, K_c = equilibrium constant]
• If Q > K_c, Q will tend to decrease so as to become equal to K. As a result, the reaction will proceed in the backward direction.
• If Q < K_c, Q will tend to increase so as to become equal to K. As a result, the reaction will proceed in the forward direction.

Calculating the Equilibrium Concentration
1. From Equilibrium Constant
Degree of dissociation of an equilibrium involving gas can be calculated by knowing the equilibrium constant and the concentration of the gaseous reactant/product.
For example, in the decomposition of carbonate, the number of moles of carbon dioxide can be calculated from the equilibrium constant by assuming an ideal gas behavior.
CaCO₃ ⇌ CaO + CO₂ Kp = [pco₂]
The decomposition of ammonia gas:

Number of moles at equilibrium = C(1 – 2α) + Cα + 3Cα = C(1 + 2α)
Partial pressure of ammonia = C(1 – 2α) / C(1 + 2α) = [(1 – 2α) / (1 + 2α)] Pt (Pt is the total presure)
Partial pressure of nitrogen = C_α / C(1 + 2α) = [α / (1 + 2α)]Pt
Partial pressure of hydrogen = 3C_α / C(1 + 2α) = [3α / (1 + 2α)]Pt
K_p = [pN₂][pH₂]³ / [pNH₃]²
K_p = [[pN₂][pH₂]³] / [pNH₃]²
= [{α / [1 + 2α]} Pt {3α / [1 + 2α]}³] / [{1 − 2α / [1 + 2α]Pt}²]
= 27α⁴ Pt² / [[1 + 2α]²[1 − 2α]²]
= 27α⁴ Pt² / 1 – 4α²
Knowing Kp and the total pressure degree of dissociation of ammonia can be calculated.
2. From Vapour Density Measurements

• Vapour Density and Number of Moles
  For ideal gases, pV = nRT = [ω / M] × RT
  M = [ωRT] / VP = ρ [RT] / P = ρ[RTV] / RTn = ρ V / n = 2 × Vapour Density
  Vapour density = ρ × V / 2n = α × 1 / n
  At equilibrium V and ρ are constant and Vapour Density is α × 1 / n
• Vapour Density and Equilibrium
  Vapour density at start / vapour density at equilibrium = D / d = M / m = Moles at equilibrium / Moles at start.
  M = initial molecular weight and m = molecular weight at equilibrium

Example: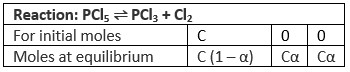

Number of moles at equilibrium = C (1 – α) + Cα + Cα = C (1 + α)
C (1 + α) C = D/d : 1 + α
α = D / d – 1
Knowing D and d, or M and m, α can be calculated.

Equilibrium Constant, Reaction Quotient and Gibbs Free Energy
K is the ratio of the relative amount of products to reactants at equilibrium while Q is the ratio at any point of time of the reaction. The Q value can be compared to K to determine the direction of the reaction to take place. The spontaneity of the process is related to the free energy change. △G (Gibbs Free Energy), K (Equilibrium Constant), and Q (Reaction Quotient) are related as follows:

1. △G < 0 and Qc ˂ Kc or Kp at the start of the reaction: The reaction will proceed to form products.
2. △G = 0 and Qc = Kc or Kp at equilibrium and no more changes in the concentration of the mixture.
3. △G > 0 and Qc > Kc or Kp after equilibrium: The reaction will proceed in the direction to form reactants.

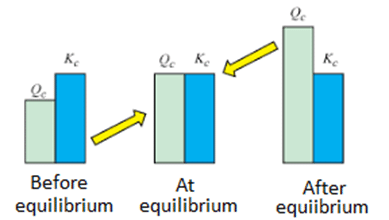Equilibrium Constant vs Reaction Quotient

(i) Kc = Equilibrium constant measured in moles per liter.
(ii) Kp = Equilibrium constant calculated from the partial pressures

Relationship between kc and kp
Consider the following reversible reaction: cC + dD ⇒ aA + bB
The equilibrium constant for the reaction expressed in terms of the concentration (mole/litre):

If the equilibrium involves gaseous species, then the concentrations are replaced by partial pressures of the gaseous substances. The equilibrium constant in terms of partial pressures is:

Where pA, pB, pC and pD represents the partial pressures of the substance A, B, C and D respectively. If gases are assumed to be ideal, then according to ideal gas equation:
pV = nRT or p = nRT/V
Where,

• p is the pressure in Pa,
• n is the number of moles of gas,
• V is the volume in m³,
• T is the temperature in Kelvin,
• n / V = molar concentration = [C]

If C is in mol dm³ and p is in bar, then R = 0.0831 bar dm³ mol^-1 K^-1 or p = CRT
Substituting for pressure, in terms of concentration:
pA = [A] RT; pB = [B] RT; pC = [C] RT and pD = [D] RT
Substituting these values in expression for Kp:






Where, △n = (c + d) – (a + b)  i.e. number of moles of gaseous products – number of moles of gaseous reactants in the balanced chemical reaction.