Escape Velocity | Physics Class 11 - NEET PDF Download
7.3 Projection of Satellites and Spaceships From Earth
To project a body into space, first it should be taken to a height where no atmopshere is present then it is projected with some initial speed. The path followed by the body also depends on the projection speed. Lets discuss the cases step by step.
Consider the situation shown in figure. A body of mass m is taken to a height h above the surface of earth to a point A and then projected with an insertion velocity vp as shown in figure.
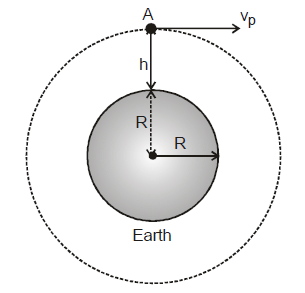
If we wish to launch the body as an earth's satellite in circular path the velocity of projection must be
...(1)
If h is small compared to radius of earth, we have
v1 = vp = = 7.93 km/s.
This velocity v1 = 7.93 km/s with which, when a body is thrown from earth's surface tangentially so that after projection it becomes a satellite of earth in a circular orbit around it, is called orbital speed or first cosmic velocity.
We've already discussed that if projection speed is lesser the orbital speed, body will start following the inner ellipse and if velocity of projection is increased the body will follow the outer ellipse. If projection speed of the satellite is further increased, the outer ellipse will also become bigger and at a particular higher projection speed, it may also be possible that body will go to infinity and will never come back to earth again.
We have discussed that negative total energy of body shows its boundness. If we write the total energy of a body projected from point A as shown in figure is
If after projection body becomes a satellite of earth then it implies it is bounded to earth and its total energy is negative. If at point A, that much of kinetic energy is imparted to the body so that total energy of body becomes zero then it implies that the body will reach to infinity and escape from gravitational field of earth. If vII is such a velocity then we have
or .......(2)
For h << Re, we have .......(3)
Thus from earth's surface a body is thrown at a speed of 11.2 km/s, it will escape from earth's gravitation. If the projection speed of body is less than this value total energy of body is negative and it wil orbit the earth in elliptical orbit. This velocity is referred as the second cosmic velocity or escape velocity. When a body is thrown with this speed, it follows a parabolic trajectory and will become free from earth's gravitational attraction.
When body is thrown with speed more then vII then it moves along a hyperbolic trajectory and also leaves the region where the earth's gravitational attraction acts. Also when it reaches infinity some kinetic energy will be left in it and it becomes a satellite of sun, that is small artificial planet.
All the calculations we've performed till now do not take into account the influence of the sun and of the planets on the motion of the projected body. In other words we have assumed that the reference frame connected with the earth is an inertial frame and the body moves relative to it. But in reality the whole system body and the earth is in a non inertial frame which is permanently accelerated relative to sun.
Lets take some examples to understand some basic concepts related to gravitational energy and projection.
Ex.14 A spaceship is launched into a circular orbit close to the earth's surface. What additional velocity has now to be imparted to the spaceship in the orbit of overcome the gravitational pull. (Radius of the earth = 6400 km and g = 9.8 m/sec.)
Sol. In an orbit close to earth's surface velocity of space ship is
We know escape velocity is
Hence additional velocity required to be imparted is Dv = vII - v
= ( - 1)
= 3.28 × 103 m/s
Ex.15 A particle is fired vertically upward with a speed of 9.8 km/s. Find the maximum height attained by the particle. Radius of the earth = 6400 km and g at the surface = 9.8 m/s2. Consider only earth's gravitation.
Sol. Initial energy of particle on earth's surface is
If the particle reaches upto a height h above the surface of earth then its final energy will only be the gravitational potential energy.
According to energy conservation, we have
Et = Ef
or or
or = (27300 - 6400) × 103 = 20900 km
Ex.16 A satellite of mass m is orbiting the earth in a circular orbit of radius r. It starts losing energy slowly at a constant rate C due to friction. If Me and Re denote the mass and radius of the earth respectively, show the the satellite falls on the earth in a limit t given by
Sol. Let velocity of satellite in its orbit of radius r be v then we have
When satellite approaches earth's surface, if its velocity becomes v', then it is given as
The total initial energy of satellite at a distance r is
The total final energy of satellite at a distance Re is
As satellite is loosing energy at rate C, if it takes a time t in reaching earth, we have
=
⇒ t =
Ex.17 An artifical satellite is moving in a circular orbit around the earth with a speed equal to half the magnitude of escape velocity from the earth.
(i) Determine the height of the satellite above earth's surface.
(ii) If the satellite is stopped suddenly in its orbit and allowed to fall freely onto the earth, find the speed with which it hits the surface of the earth.
Sol. (i) Let M and R be the mass and radius of the earth respectively. If m be the mass of satellite, then escape velocity from earth vc =
velocity of satellite =
Further we know orbital speed of satallite at a height h is
or
From equation written above, we get
h = R = 6400 km
(ii) Now total energy at height h = total energy at earth's surface (principle of conservation of energy)
or
or [As h = R]
Solving we get
or = 7.919 km/s
|
95 videos|367 docs|98 tests
|
FAQs on Escape Velocity - Physics Class 11 - NEET
| 1. What is escape velocity? |  |
| 2. How is escape velocity calculated? |  |
| 3. Can escape velocity vary for different celestial bodies? |  |
| 4. What happens if an object reaches escape velocity? |  |
| 5. How is escape velocity related to space exploration? |  |

















