Examples: Electricity | Science Class 10 PDF Download
Examples with Solutions - Electricity, Class 10, Science
Q1. A piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R', then the ratio R/R' is :
(A) 1/25 (B) 1/5 (C) 5 (D) 25
Ans. Resistance of each one of the five parts =
Resistance of five parts connected in parallel is given by
or
or 25
Thus, (D) is the correct answer.
Q2. Which of the following terms does not represent electrical power in a circuit :
(A) I2R (B) IR2 (C) VI (D) V2/R
Ans. Electrical power, P = VI = (IR) R = t2R = V
Obviously, IR2 does not represent electrical power in a circuit.
Thus, (B) is the correct answer.
Q3. An electric bulb is rated 220 V and 100 W. When it is operated on 110 V, the power consumed will be:
(A) 100 W (B) 75 W (C) 50 W (D) 25 W
Ans. Resistance of the electric bulbs, R = (P = V2/R)
or R = = 484W
Power consumed by the bulb when it is operated at 110 V is given by
P' = (V' = 100 V)
Thus, (D) is the correct answer.
Q4. Two conducting wires of the same material and of equal lengths and equal diameters are first connected in series and then in parallel in an electric circuit. The ratio of the heat produced in series and parallel combinations would be :
(A) 1:2 (B) 2:1 (C) 1:4 (D) 4:1
Ans. Since both the wires are made of the same material and have equal lengths and equal diameters, these have the same resistance. Let it be R.
When connected in series, their requivalent resistance is given by
Rs = R + R = 2R
When connected in parallel, their equivalent resistance is given by
or Rp =
Further, electrical power is given by P =
Power (or heat produced) in series, Ps =
Power (or heat produced) in parallel, Pp =
Thus,
or Ps : Pp : : 1 : 4
Thus, (C) is the correct answer.
Q5. How is voltmeter connected in the circuit to measure potential difference between two points?
Ans. A voltmeter is always connected in parallel across the points between which the P.D. is to be determined.
Q6. A copper wire has a diameter of 0.5 mm and a resistivity of 1.6 × 10-6 ohm cm. How much of this wire would be required to make a 10 ohm coil? How much does the resistance change if the diameter is doubled?
Ans. We are given that, Diameter of the wire, D = 0.5 mm = 0.5 × 10-3 m
resistivity of copper, r = 1.6 × 10-6 ohm cm = 1.6 × 10-8 ohm m
required resistance, R = 10 ohm
As R = , l = [A = pr2 = p(D/2)2 = pD2/4]
or l = m = 112.7 m
Since, R = , R ∝ 1/D2. When D is doubled, R becomes times.
Q7. The values of current, I, flowing in a given resistor for the corresponding values of potential difference, V, across the resistor are given below :
I (ampere) : 0.5 1.0 2.0 3.0 4.0
V (volt) : 1.6 3.4 6.7 10.2 13.2
Plot a graph between V and I and calculate the resistance of the resistor.
Ans. The V-I graph is as shown in fig.
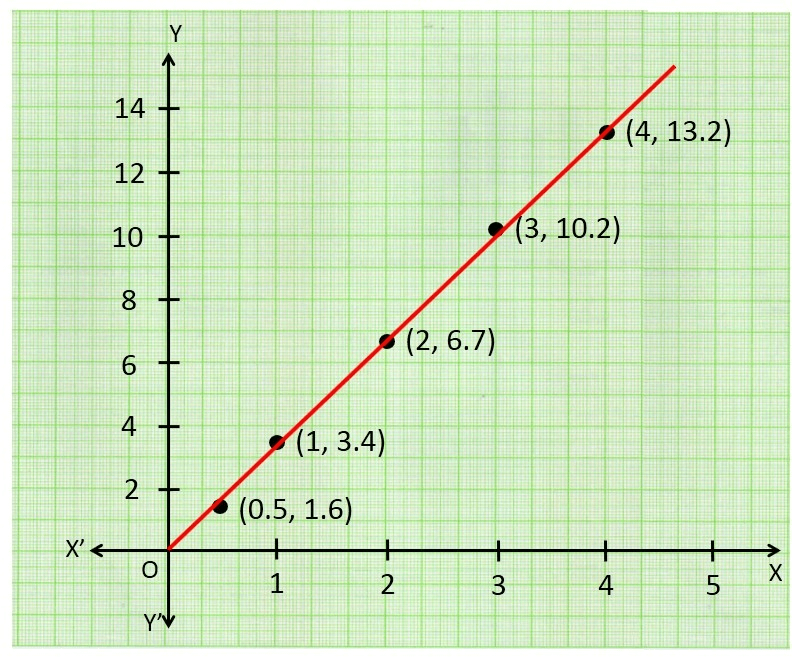
For V = 4V (i.e., 9V - 5V), I = 1.25 A (i.e., 2.65 A - 1.40 A). Therefore, R = = 3.2 Ω
The value of R obtained from the graph depends upon the accuracy with which the graph is plotted.
Q8. When a 12 V battery is connected across an unknown resistor, there is a current of 2.5 mA in the circuit. Find the value of the resistance of the resistor.
Ans. Here, V = 12 V, I = 2.5 mA = 2.5 × 10-3 A
Resistance of the resistor, R = = = 4800 Ω = 4.8 kΩ
Q9. A battery of 9 V is connected in series with resistors of 0.2Ω, 0.3Ω, 0.4Ω, 0.5Ω and 12Ω. How much current would flow through the 12Ω resistor?
Ans. Since all the resistors are in seies, equivalent resistance,
Rs = 0.2 Ω + 0.3 Ω + 0.4 Ω + 0.5 Ω + 12 Ω= 13.4 Ω
Current through the circuit, I =
In series, same current (I) flows through all the resistors. Thus, current flowing through 12 Ω resistor = 0.67 A
Q10. How many 176 Ω resistors (in parallel) are required to carry 5 A in 220 V line?
Ans. Here, I = 5A, V = 220 V.
Resistance required in the circuit, R = , Resistance of each resistor, r = 176 Ω
If n resistors, each of resistance r, are connected in parallel to get the required resistance R, then R =
or 44 = or n =
= 4
Q11. Show how you would connect three resistors, each of resistance 6W, so that the combination has a resistance of (i) 9Ω (ii) 2Ω.
Ans. (i) In order to get a resistance of 9 W from three resistors, each of resistance 6 W, we connect two resistors in parallel and this parallel combination (or resistance 3W) in series with the third resistor as shown in fig.
(ii) In order to get a resistance of 2W from three resistors, each of resistance 6 W, we connect all the three resistors in parallel as shown in fig (b) as equivalent resistance in parallel combination, i.e., Rp is given by Rp = = 2W.
Q12. Several electric bulbs designed to be used on a 220 V electric supply line, are rated 10 W. How many lamps can be connected in parallel with each other across the two wires of 220 V line if the maximum allowable current is 5 A?
Ans. Resistance of each bulb, r =
Total resistance in the circuit, R
Let n be the number of bulb (each of resistance r) to be connected in parallel to obtain a resistance R.
Clearly, R = or n =
Q13. A hot plate of an electric oven connected to a 220 V line has two resistance coils A and B, each of 24Ω resistance, which may be used separately, in series, or in parallel. What are the currents in the three cases?
Ans. Here, potential difference, V = 220 V
Resistance of each coil, r = 24 Ω
(i) When each of the coils A or B is connected separately, current through each foil, i.e.,
I =
(ii) When coils A and B are connected in series, equivalent resistance in the circuit,
Rs = r + r = 2r = 48Ω
Current through the series combination, ie.e, Is =
(iii) When the coils A and B are connected in parallel, equivalent resistance in the circuit,
Rp =
Current through the parallel combination, ie.e, Ip =
Q14. Compare the power used in the 2Ω resistor in each of the following circuits :
(i) a 6 V battery in series with 1Ω and 2Ω resistors, and (ii) a 4 V battery in parallel with 12W and 2W resistors.
Ans. (i) Since 6 V battery is in series with 1Ω and 2Ω resistors, current in the circuit,
I =
Power used in 2W resistor, P1 = I2R = (2A)2 × 2W = 8W
(ii) Since 4 V battery is in parallel with 12W and 2W resistors, pd across 2W resistor, V = 4V.
Power used in 2W resistor, P2 =
Clearly,
Q15. Two lamps, one rated 100 W at 220 V, and the other 60 W at 220 V, are connected in parallel to the electric mains supply. What current is drawn from the line if the supply voltage is 220 V?
Ans. Resistance of first lamp, r1 =
resistance of the second lamp, r2 =
Since the two lamps are connected in parallel, the equivalent resistance is given by
or Rp = = 302.6 Ω
Current drawn from the line, i.e., I = = 0.73 A
Q16. Which uses more energy, a 250 W TV set in 1 h, or a 1200 W toaster in 10 minutes?
Ans. Energy used by 250 W TV set in 1 h = 250 W × 1h = 250 Wh
Energy used by 1200 W toaster in 10 min. (i.e., 1/6 h) = 1200 W × (1/6) h = 200 Wh
Thus, a 250 W TV set uses more power in 1 h than a 1200 W toaster in 10 minutes.
Q17. An electric heater of resistance 8W draws 15 A from the service mains for 2 hour. Calculate the rate at which heat is developed in the heater.
Ans. Here, I = 15A, R = 8 Ω, t = 2h
Rate at which heat is developed, i.e, electric power, P = I2 R = (15)2 × 8 = 1800 W = 1800 J/s
Q18. Explain the following
(a) Why is tungsten used almost exclusively for filament of incandescent lamps?
(b) Why are the conductors of electric heating devices, such as toasters and electric irons, made of an alloy rather than a pure metal?
(c) Why is the series arrangement not used for domestic circuits?
(d) How does the resistance of a wire vary with its cross-sectional area?
(e) Why are copper and aluminium wires usually employed for electricity transmission.
Ans. (a) Tungsten has a high melting point (3380°C) and becomes incandescent (i.e., emits light at a high temperature) at 2400 K.
(b) The resistivity of an alloy is generally higher than that of pure metals of which it is made of.
(c) In series arrangement, if any one of the appliances fails or is switched off, all the other appliances stop working because the same current is passing through all the appliances.
(d) The resistance of a wire (R) varies inversely as its cross-sectional area (A) as R ∝ 1/A.
(e) Copper and Aluminium wires possess low resistivity and as such are generally used for electricity transmission.
|
80 videos|567 docs|80 tests
|
FAQs on Examples: Electricity - Science Class 10
| 1. What is electricity? |  |
| 2. How is electricity generated? |  |
| 3. What are the different types of electric circuits? |  |
| 4. What is the difference between AC and DC electricity? |  |
| 5. How can electricity be dangerous? |  |

















