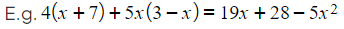Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Expanding Brackets
Expanding Brackets | Mathematics for GCSE/IGCSE - Class 10 PDF Download
| Table of contents |

|
| Expanding One Bracket |

|
| Expand & Simplify |

|
| Expanding Double Brackets |

|
| Expanding Triple Brackets |

|
Expanding One Bracket
How do I expand a bracket?
- The expression 3x(x + 2) means 3x multiplied by the bracket (x + 2).
- Here, 3x is the term outside the bracket (referred to as a "factor"), and x + 2 are the terms inside the bracket.
- Expanding the brackets involves multiplying the term on the outside by each term on the inside, which eliminates the brackets.
- 3x(x + 2) expands to 3x x x + 3x x 2, which simplifies to 3x2 + 6.
Beware of minus signs
- Remember the basic rules of multiplication with signs
- − × − = +
- − × + = −
- It helps to put brackets around negative terms
Expand & Simplify
How to simplify an expression with multiple terms in brackets?
- Identify two or more terms enclosed in brackets in the expression that are being added or subtracted. For instance, if you see two sets of brackets connected by a plus or minus sign, you are not multiplying the brackets together.
- For example, consider the expression:
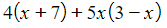
- For example, consider the expression:
- Step 1: Expand each set of brackets individually by multiplying the term outside the brackets with each term inside. Pay attention to handling negative terms correctly.
- E.g. the first set of brackets expands to 4 x x + 4 x 7, and simplifies to 4x + 28, the second set of brackets expands to
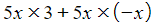 and simplifies to
and simplifies to 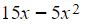
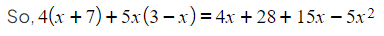
- E.g. the first set of brackets expands to 4 x x + 4 x 7, and simplifies to 4x + 28, the second set of brackets expands to
- Step 2: Combine like terms after expanding the brackets.
Expanding Double Brackets
- Every term in the first bracket must be multiplied by every term in the second bracket. To expand (x + 1)(x + 3), you will need 4 multiplications in total.
- A good way to remember all the multiplications is using the acronym FOIL:
- F = First: Multiply together the first terms in each bracket.
- O = Outside: Multiply the first term in the first bracket by the second term in the second bracket (visually, these are the "outer" terms).
- I = Inside: Multiply the second term in the first bracket by the first term in the second bracket (visually, these are the "inner" terms).
- L = Last: Multiply together the last terms in each bracket.
- It is beneficial to enclose negative terms in brackets when multiplying.
- Simplify the final answer by combining like terms if present.
How do I expand two brackets using a grid?
- To expand (x + 1)(x + 3), represent the brackets as headings in a grid.
- For each cell in the grid, multiply the term in the row heading by the term in the column heading.
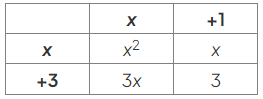
- Add all the terms inside the grid to calculate the answer.
- x2 + x + 3x + 3
- Collect like terms to simplify the final expression.
- x2 + 4x + 3
How do I expand a bracket squared?
- Write (x + 3)2 as (x + 3)(x + 3) and use one of the methods above
- for example, with FOIL: (x + 3)(x + 3) = x2 + 3x + 3x + 9
- collect like terms to get the final answer
- x2 + 6x + 9
- Do not make the common mistake of saying (x + 3)2 is x2 + 32
- This cannot be true, as substituting x = 1, for example, gives (1 + 3)2 = 42 = 16 on the left, but 12 + 32 = 1 + 9 = 10 on the right
Expanding Triple Brackets
How to Expand Three Brackets?
- Multiply out any two brackets using a standard method and simplify the answer by collecting like terms.
- Combine the two brackets into a single long bracket containing the expanded result.
- Proceed to expand this long bracket with the third (unused) bracket.
- The process typically resembles multiplying expressions like (x + a)(x2 + bx + c).
- Each term in the first bracket should be multiplied with every term in the second bracket, resulting in a total of six terms.
- Using a grid can aid in keeping track of all six terms.
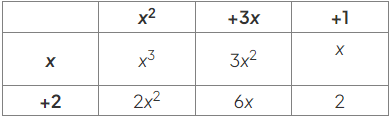
- For instance, for expressions like (x + 2)(x2 + 3x + 1), adding terms in the grid (diagonals represent like terms) gives x3 + 2x2 + 3x2 + 6x + x + 2.
- Combine like terms to obtain the final answer of x3 + 5x2 + 7x + 2.
- Ensure to simplify the final answer further by collecting any remaining like terms, putting negative terms in brackets when multiplying.
The document Expanding Brackets | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|413 docs|19 tests
|
FAQs on Expanding Brackets - Mathematics for GCSE/IGCSE - Class 10
| 1. How do you expand brackets in algebraic expressions? |  |
Ans. To expand brackets in algebraic expressions, you need to multiply each term inside the brackets by the term outside the brackets. Then, simplify the expression by combining like terms.
| 2. What is the FOIL method used for when multiplying binomials? |  |
Ans. The FOIL method is used to multiply two binomials together. FOIL stands for First, Outer, Inner, Last, and it helps you remember the order in which you should multiply the terms in each binomial.
| 3. How do you expand double brackets in algebraic expressions? |  |
Ans. To expand double brackets in algebraic expressions, you can use the FOIL method by multiplying each term from the first bracket with each term from the second bracket. Then, simplify the expression by combining like terms.
| 4. Why is it important to understand how to expand and simplify algebraic expressions? |  |
Ans. Understanding how to expand and simplify algebraic expressions is important because it allows you to manipulate and work with algebraic equations more effectively. This skill is essential for solving equations, simplifying complex expressions, and applying algebra in real-world problems.
| 5. How can expanding brackets help in solving mathematical problems? |  |
Ans. Expanding brackets is a fundamental skill that allows you to simplify and manipulate algebraic expressions. It helps in solving mathematical problems by breaking down complex expressions into simpler forms, making it easier to evaluate and solve equations.
Related Searches