Exponents and Power | Mathematics for Digital SAT PDF Download

Exponent and power are terms used when a number is multiplied by itself a specific number of times. The difference between exponents and power is an extremely minor observation that most of the time is neglected. There is a very thin line of difference between exponent and power. We will be understanding exponents and powers along with their difference in this article.

What are Exponent and Power?

When a number is multiplied by itself a finite number of times, the number being multiplied is called the base number, and the number of times it is being multiplied is called the exponent. Suppose a number is being multiplied by itself n number of times, then this expression is called the nth power of the given number. So, to summarize, we can say that an exponent is the number of times a given number is being multiplied by itself and power is the value of the product of the base number raised to an exponent.

Difference between Exponent and Power

Exponential notation or the exponential form of numbers helps us to express and represent extremely large and small numbers in a very convenient way. For example, 10000000000000 can be represented as 1 × 10¹³ whereas 0.0000000000000007 can be represented as 7 × 10^-16. This improves the readability of numbers and helps us to maintain the accuracy of numbers and saves our time. Before going into the difference between exponent and power, let's understand what is an exponent and power.

Exponent and Power Meaning

Let us take an example to understand the definition of exponent and power. Consider 6 × 6 × 6 × 6. We know that, in exponential form, 6 × 6 × 6 × 6 can be written as 6⁴ since the number 6 is getting multiplied by itself four times. The exponent of a number is defined as the number of times a number is multiplied by itself.
Here, in 6 × 6 × 6 × 6, the number 6 is multiplied by itself four times which is also represented as 6⁴. Here, 6 is the base, and 4 is the exponent. Power is defined as the whole expression of repeated multiplication that includes the base and the exponent. In the given example 6 × 6 × 6 × 6, the exponential form is 6⁴. We can say this as "6 raised to the power of 4" where 6 is the base and 4 is the exponent. In other words, 6⁴ is called the 4^th power of 6. Hence, the definition of power is for the whole expression of exponential form.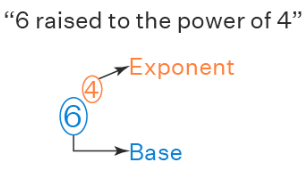

Exponent Vs Power

Let us now tabulate the difference between exponent and power as shown below.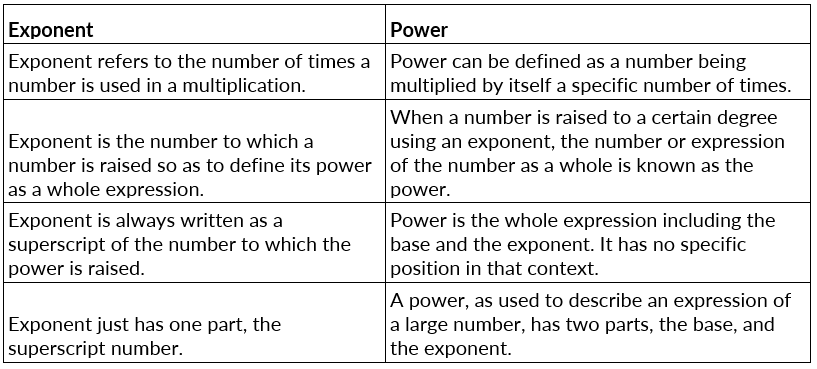

Important Notes on Exponent and Power

• An exponent is the number of times a given number is being multiplied by itself.
• The expression when a number is being multiplied by itself n number of times is called the n^th power of the given number.

Example: Find the value of 2⁵.
Solution: In the given expression 2⁵, we have the base 2 and the exponent is 5.
Also, we can say that 2 is raised to the power of 5. Let's expand 2⁵.
It can be written as 2 × 2 × 2 × 2 × 2 = 32.
Thus, the value of 2⁵ is 32.