Expressing Concentration of Solutions | Chemistry Class 12 - NEET PDF Download
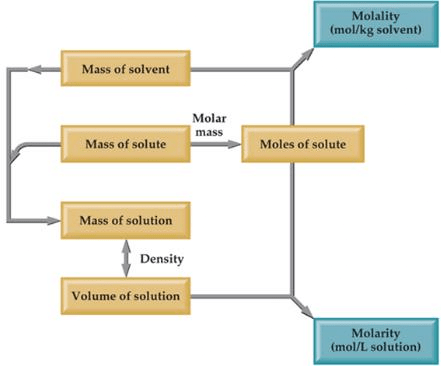
What is Expression of Concentration of Solution?
We always discuss a solution being diluted or concentrated; this is a qualitative way of expressing the concentration of the solution. A dilute solution means the quantity of solute is relatively very small, and a concentrated solution implies that the solution has a large amount of solute. But these are relative terms and do not give us the quantitative concentration of the solution.
So, to quantitatively describe the concentrations of various solutions around us, we commonly express levels in the following way, let’s study each method and determine the formulas for this method:
- Percent by weight
- Percent by volume
- Percent by weight/volume
- Molarity
- Molality
- Normality
- Mole Fraction
- Parts per Million
- Formality
- Strength (g/L)
- Molarity of mixing
(i) Mass/Weight Percentage or Percentage by Mass/Weight
It is the amount of solute in grams present in 100 grams of the solution.
Therefore, the formula will be: The ratio mass of solute to the mass of the solvent is the mass fraction. Thus, the mass percentage of solute = Mass fraction × 100.
The ratio mass of solute to the mass of the solvent is the mass fraction. Thus, the mass percentage of solute = Mass fraction × 100.
10% solution of sugar by mass means that 10 grams of sugar is present in 100 grams of the solution, i.e., we have dissolved 10 grams of sugar in 90 grams of water.
Example: If 11 g of oxalic acid are dissolved in 500 mL of solution (density = 1.1 g mL-¹), what is the mass % of oxalic acid in solution?
Solution:11 g of oxalic acid are present in 500 mL of solution.
Density of solution = 1.1 g mL-¹
Mass of solution = (500 mL) x (1.1. g mL-¹) = 550 g
Mass of oxalic acid = 11 g
Mass% of Oxalic Acid = 11÷550 ✖ 100 % = 2%
(ii) Volume Percentage
It is the volume of solute in mL present in 100 mL solution.
The formula will be:
Volume Percentage = Volume of solute/Volume of Solution × 100 10% solution of HCl by volume means that 10 mL of liquid HCl is present in 100 mL of the solution.
10% solution of HCl by volume means that 10 mL of liquid HCl is present in 100 mL of the solution.
Example: Calculate the percent volume of solute if 5 ml of it is dissolved in a solvent of 90 ml.
Solution:Volume of Solute (v) = 5 ml
Volume of Solvent = 90 ml
Volume of Solution (V) = (5 + 90) ml = 95 ml
Using the formula,
P = (v / V) × 100
P = (5/95) × 100
P = 5.26 %
(iii) Mass by Volume Percentage
It is the mass of solute present in 100 mL of solution. We can calculate the mass of the solute using the volume percentage.
 The formula would be:
The formula would be:
Mass by Volume Percentage = Mass of Solute/Volume of Solution × 100
It changes on changing temperature.
Example: Calculate the concentration in terms of mass by volume percentage of the solution containing, 3g of potassium chloride in 75ml of potassium chloride (KCl) solution.
Solution:Mass of solute =3 g
Volume of solution =75 ml
Mass by volume % =  =3/75×100=4 %
=3/75×100=4 %
(iv) Molarity
The molarity of a solution gives the number of gram molecules of the solute present in one litre of the solution.
Molarity(M) = number of moles of solute/Volume of Solution in L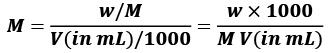
 w = Mass of solute in grams
w = Mass of solute in grams- M = molecular weight of solute in gm/mol.
- V = volume of solution in ml.
- 1 mol L-1 solution of KCl means that 1 mol of KCl is dissolved in 1 L of water.
Unit of molarity: mol L-1 - Molarity is the most common way of representing the concentration of the solution.
- Molarity is dependent on temperature as M ∝ 1/T
- When a solution is diluted (x times), its molarity also decreases (by x times)
Example: Calculate the molarity of a solution containing 5 g of NaOH in 450 mL solution.
Solution: Moles of NaOH = 5g/40 g mol-1 = 0.125 mol
Volume of the solution in litres = 450 mL / 1000 mL L-1
Using equation (2.8),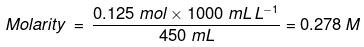 = 0.278 mol L–1
= 0.278 mol L–1
= 0.278 mol dm–3
(V) Molality
Molality of a solution is the number of moles of solute dissolved in 1 Kg of the solvent.
Molality (m) = Number of moles of solute/Mass of Solvent in Kg
- w = mass of solute in grams
- M = molecular wt of solute
- W = mass of solvent in gram.
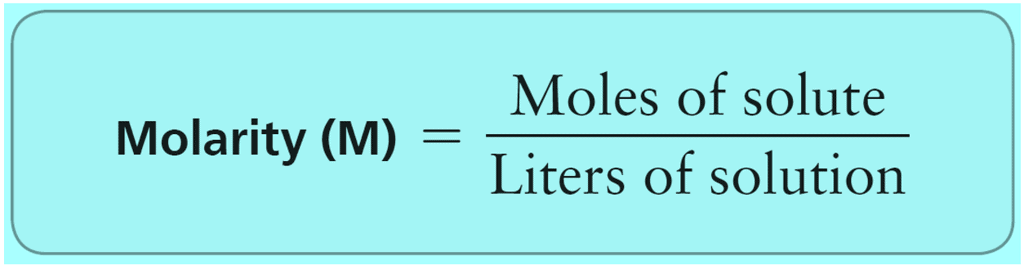
Thus, if one gram molecule of a solute is present in 1 kg of the solvent, the concentration of solutions is said to be one molal.
The unit of molarity is mol kg-1.
Molality is the most convenient method to express the concentration of solutions because it involves the mass of liquids rather than their volumes. It is also independent of the variation in temperature.
Example: Calculate the molality of 2.5 g of ethanoic acid (CH3COOH) in 75 g of benzene.
Solution: Molar mass of C2H4O2 : 12 × 2 + 1 × 4 + 16 × 2 = 60 g mol–1
Moles of C2H4O2 = 2.5/60 g mol-1 = 0.0417 mol
Mass of benzene in kg = 75 g/1000 g kg–1 = 75 × 10–3 kg
Molality of C2H4O2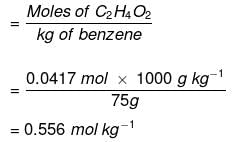
(vi) Normality
The normality of a solution gives the number of gram equivalents of the solute present in one litre of the solution.

Normality (N) = Number of gram equivalent of solute/Volume of Solution in L
Equivalent mass = Molar mass/n - factor
No. of equivalent = Mass of solute/equivalent mass = No. of moles of solute x n - factor
= No. of moles of solute x n - factor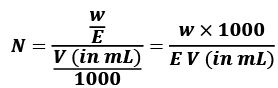
w = mass of solute in gram
V = volume of solution in ml
E = equivalent wt of solute
Thus, if one gram equivalent of a solute is present in one litre of the solution, the concentration of solutions is said to be 1 normal.
- 1N = Normal = One gram equivalent of the solute per litre of solution = Normality is 1
- N/2 = Seminormal = 0.5 g equivalent of the solute per litre of solution = Normality is 0.5
- N/10 = Decinormal = 0.1 g equivalent of the solute per litre of solution = Normality is 0.1
- N/100 = Centinormal = 0.01 g equivalent of the solute per litre of solution = Normality is 0.01
- N/1000 = Millinormal = 0.001 g equivalent of the solute per litre of solution = Normality is 0.001
Relationship between normality and other Concentration Terms - Molarity × Molecular mass= Strength of the solution (g/L)
- Normality × Equivalent mass = Strength of the solution (g/L)
- Molarity × Molecular mass= Normality x Equivalent mass
- Normality = n × Molarity
Example: Calculate the normality of a 310 mL NaOH solution made by dissolving 0.4 gram of NaOH.
Solution: The formula to calculate the normality is,
Normality (N) = Number of gram equivalents / Volume of the solution in liters
Number of gram equivalents = weight of solute / Equivalent weight of solute
Equivalent weight of solute = 23+16+1 = 40
Since,
Normality (N) = weight of solute / Volume of the solution in liters × Equivalent weight of solute
N = (4/40) × (1000/310)
= 0.1 × 3.2258
= 0.3225 N
(vii) Mole Fraction
Mole fraction can be defined as the ratio of a number of moles of the component in the solution to the total number of moles of all components in the solution.
- It is denoted by the alphabet x and subscript written on the right-hand side of x denotes the component of which mole fraction is being calculated.
- Mathematically, Mole fraction of a component =
Number of moles of the component/Total number of moles of all components - Let us consider a binary mixture of A and B. let the number of moles of A and B be nA and nB respectively, then
Mole fraction of A = xA = nA/ nA + nB
Mole fraction of B = xB = nA/ nA + nB - For a solution where a number of components = i


- In a given solution sum of the mole fractions of all the components is
unity.
Mathematically, x1 + x2 + x3 …. + xi =1
Example : Calculate the mole fraction of ethylene glycol (C2H6O2) in a solution containing 20% of C2H6O2 by mass.
Solution: Assume that we have 100 g of solution (one can start with any amount of solution because the results obtained will be the same). The solution will contain 20 g of ethylene glycol and 80 g of water.
Molar mass of C2H6O2 = 12 × 2 + 1 × 6 + 16 × 2 = 62 g mol–1
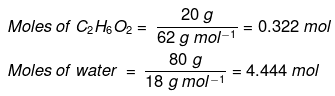
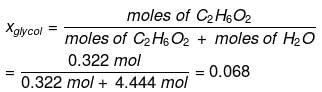
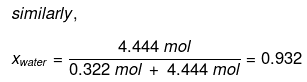
Mole fraction of water can also be calculated as: 1 – 0.068 = 0.932.
(viii) Parts per million (ppm)
When a solute is present in trace quantities, it is convenient to express the concentration of solutions in parts per million (ppm). The formula is as follows:
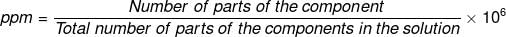 In case of mass, we may express it as:
In case of mass, we may express it as: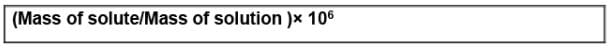
In case of volume, we may express it as:
So, we can express the concentration of solutions in parts per million as mass to mass, volume to volume and mass to volume form.
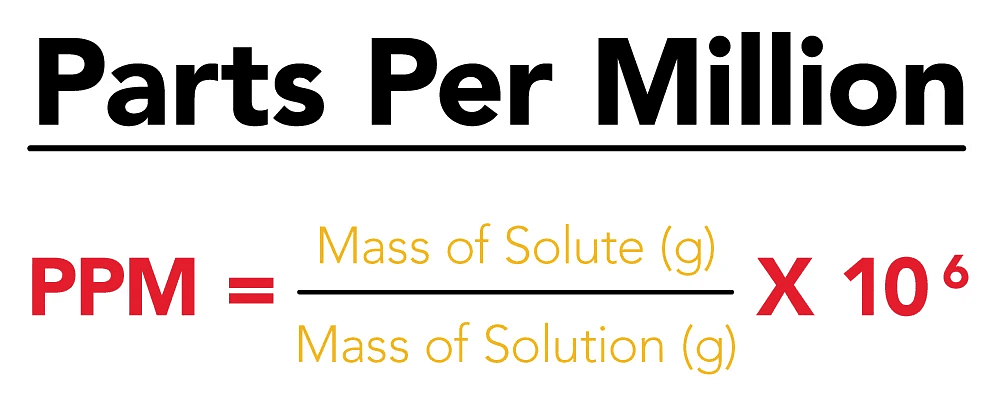
- Atmospheric pollution in cities is also expressed in ppm by volume.
- It refers to the volume of the pollutant in 106 units of volume.
- 10 ppm of SO2 in the air means 10 mL of SO2 is present in 106 mL of air.
(ix) Formality
It is the number of mass in grams present per litre of solution. In case, formula mass is equal to molecular mass, formality is equal to molarity.
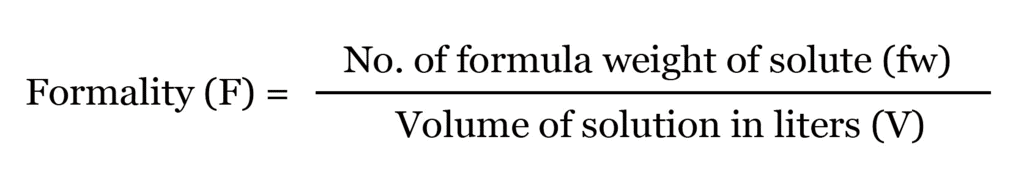
- Like molarity and normality, the formality is also dependent on temperature. It is used for ionic compounds in which there is no existence of a molecule.
- A mole of ionic compounds is called formal and molarity as the formality.
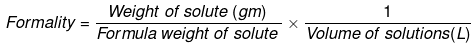
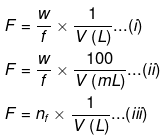
Where,
- w = weight of solute,
- f = formula weight of solute
- V= volume of solution
- nf = no. of gram formula weight
(x) Strength (g/L)
It is defined as the weight of solute per litre (1000 mL) of solution.
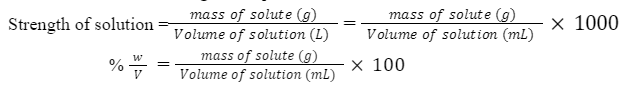
Example: 10% w/v sucrose solution, then specify its concentration in g/L.
In 100 mL solution, weight of sucrose = 10 g
Therefore, in 1000mL solution= 10/100 = 100 g
Hence strength will be 100g/L
(xi) Molarity of Mixing
Let there be three samples of solution (containing same solvent and solute) with their molarities M1 ,M2 ,M3 and volumes V1 ,V2 ,V3 respectively.These solutions are mixed; molarity of mixed solution may be given as:
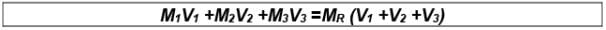
where, MR is the Resultant molarity
V1 + V2 + V3 = Resultant volume after mixing
Note: Molarity is dependent on volume; therefore, it depends on temperature.
| 1M | molar solution, i.e, molarity is l |
| 0.5 M or M/2 | Semimolar |
| 0.1 M or M/2 | Decimolar |
| 0.01 M or M/100 | Centimolar |
| 0.001 M or M/100 | Millimolar |
Dilution Formula
The dilution formula is giving by the following expression:
| M1V1 = M2V2 |

Practice Questions
Problem 1. Calculate the masses of cane sugar and water required to prepare 250 g of 25% cane sugar solution.Solution.
Mass percentage of cane sugar = 25
We know that,
Mass percentage = Mass of solute/Mass of solution × 100
25 = Mass of cane sugar/250g × 100
Mass of cane sugar = 25 ×250/100 = 62.5 g
Mass of water (250 -62.5)g = 187.5 g
Problem 2. A tank is charged with a mixture of 1.0 x 103 mol of oxygen and 4.5 x 103 mol of helium. Calculate the mole fraction of each gas in the mixture.
Solution.
The given parameters are
nHe = 4.5 x 103 mol and nO2 = 1.0 x 103 mol
Mole fraction can be calculated as
xHe = 4.5 x 103 mol / (4.5 x 103 mol + 1.0 x 103 mol)
=4.5 mol / 5.5 mol = 0.82
xO2 = 2.0 x 103 mol / (4.5 x 103 mol + 1.0 x 103 mol)
= 1.0 x 103 / 5.5 x 103
= 0.18
Problem 3. The density of a solution containing 13% by mass of sulphuric acid is 1.09 g/mL. Calculate the molarity and normality of the solution.
Solution.
Volume of 100 g of the solution
= 100/d = 100/1.09 mL
= 100/1.09 × 1000 litre
= 1/1.09 × 10 litre
Number of moles of H2so4 in 100 g of the solution = 13/98
Molarity = No. of moles of H2So4/Volume of Solu. in litre = 13/98 × 1.09 × 10/1
= 1.445 M
We know that,
Normality = Molarity × n
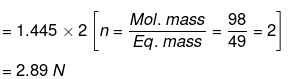
Problem 4. What is the mole fraction of carbon tetrachloride (CCl4) in solution if 3.47 moles of CCl4 is dissolved in 8.54 moles of benzene (C6H6)?
Solution.
Mole Fraction CCI4 (XCCI4) = moles of CCI4/total moles
XCCI4 = 3.47 moles CCI4/3.47 moles CCI4 + 8.54 moles C6H6
XCCI4 = 0.289
Problem 5. What is the mole fraction of formaldehyde (CH2O) in solution if 25.7 grams of CH2O is dissolved in 3.25 moles of carbon tetrachloride (CCl4)?
Solution.
The grams of acetone will need to be converted into moles in order to solve for mole fraction.
Mole Fraction CH2O(XCH2O) = moles of CH2O/total moles
XCH2O = 0.856 moles CH2O/0.856 moles CH2O + 3.25 moles CCI4
XCH2O = 0.208
Problem 6. 0.100 mole of NaCl is dissolved into 100.0 grams of pure H2O. What is the mole fraction of NaCl?
Solution.
100.0 g / 18.0 g mol-1 = 5.56 mol of H2O
Add that to the 0.100 mol of NaCl = 5.56 + 0.100 = 5.66
mol total Mole fraction of NaCl = 0.100 mol / 5.66 mol = 0.018
The mole fraction of the H2O:
5.56 mol / 5.66 mol = 0.982
Problem 7. A solution is prepared by mixing 25.0 g of water, H2O, and 25.0 g of ethanol, C2H5OH. Determine the mole fractions of each substance.
Solution.
(1) Determine the moles of each substance:
H2O ⇒ 25.0 g / 18.0 g/mol = 1.34 mol
C2H5OH ⇒ 25.0 g / 46.07 g/mol = 0.543 mol
(2) Determine mole fractions:
H2O ⇒ 1.34 mol / (1.34 mol + 0.543 mol) = 0.71
C2H5OH ⇒ 0.543 mol / (1.34 mol + 0.543 mol) = 0.29
Problem 8. A solution contains 10.0 g pentane, 10.0 g hexane and 10.0 g benzene. What is the mole fraction of hexane?
Solution.
Try it yourself Using hints given below !
(1) You need to determine the moles of pentane, hexane and benzene: to do this, you need the molecular weights. Here are the formulas:
pentane: C5H12
hexane: C6H14
benzene: C6H6
(2) When you have the moles of each, add them together.
(3) Then, divide the moles of hexane by the total.
Problem 9. The molality of an aqueous solution of sugar (C12H22O11) is 1.62m. Calculate the mole fractions of sugar and water.
Solution.
(1) Molality is moles solute / kg of solvent. Therefore we know our solution is:
1.62 mol C12H22O11
1.00 kg = 1000 g of water
(2) Calculate the moles of water present:
1000 g / 18.0152 g/mol = 55.50868 mol
(3) Determine the mole fraction of the sugar:
1.62 mol / (1.62 mol + 55.50868 mol) = 0.028357 = 0.0284 (to three sf)
(4) You can calculate the mole fraction of the water by subtraction.
Problem 10. How many grams of water must be used to dissolve 100.0 grams of sucrose (C12H22O11) to prepare a 0.020 mole fraction of sucrose in the solution?
Solution.
(1) Determine moles of sucrose:
100.0 g / 342.2948 g/mol = 0.292145835 mol
(2) Determine moles of water required to make the solution 0.020 mole fraction of sucrose:
0.020 = 0.292 / (0.292 + x)
(0.020) (0.292 + x) = 0.292
0.00584 + 0.02x = 0.292
0.02x = 0.28616
x = 14.308 mol of H2O
Comment: you can also do this:
0.292 is to 0.02 as x is to 0.98
(3) Determine grams of water:
14.308 mol x 18.015 g/mol = 258.0 g
Problem 11. Surprisingly, water (in the form of ice) is slightly soluble in liquid nitrogen. At -196 °C, (the boiling point of liquid nitrogen) the mole fraction of water in a saturated solution is 1.00 x 10-5. Compute the mass of water that can dissolve in 1.00 kg of boiling liquid nitrogen.
Solution.
(1) Use the definition of mole fraction to set up the following:
χwater = moles of water / (moles of water + moles of nitrogen)
1.00 x 10-5 = x / (x + 71.3944041)
I'm going to carry some guard digits until the end of the calculation.
(2) Some algebra: (1.00 x 10-5) (x) + 7.139440411 x 10-4 = x
0.99999x = 7.139440411 x 10-4
x = 7.139511806 x 10-4 mol of H2O
(3) Calculate grams of water from moles of water:
7.139511806 x 10-4 mol x 18.0152 g/mol = 1.2862 x 10-2 g
1.29 x 10-2 g (to three sf)
Problem 12. What is the mole fraction of cinnamic acid in a mixture that is 50.0% weight urea in cinnamic acid (urea = 60.06 g/mol; cinnamic acid = 148.16 g/mol)
Solution.
(1) Let us assume 100.0 g of this mixture are present. Therefore:
50.0 g is urea
50.0 g is cinnamic
(2) Convert grams to moles: urea:
50.0 g / 60.06 g/mol = 0.8325 mol
cinnamic acid: 50.0 g / 148.16 g/mol = 0.3375 mol
(3) Determine mole fraction of cinnamic acid:
0.3375 mol / 1.1700 mol = 0.2885
Problem 13. 5 g of NaCl is dissolved in 1000 g of water. If the density of the resulting solution is 0.997 g per cc, calculate molality, molarity, normality and mole fraction of the solute.
Solution.
Mole of NaCl = 5/58.5 = 0.0854 (Mol. wt. of NaCl = 58.5)
Molality = Moles/Wt. of solvent in gram x 1000
= 0.0854/1000 x 1000 = 0.0854 m
Volume of the solution= Wt. of solution in gram/Density in gram / cc
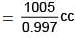
Again by definition
Molarity = Moles/Volume of solution in litre
= 0.0854/1.008
= 0.085 M
∴ Normality = 0.085 N (for NaCl, eq. wt. = mol. wt)
Further, Mole of H2O = 1000/18 = 55.55
(1000 gram of water = 1000 ml of water, because density = 1 g/cc)
Total mole = Mole of NaCl + Mole of H2O
= .0854 + 55.55 = 55.6354
Mole fraction of NaCl = 7.85/98.66 = 0.0854/55.6409 = 1.535 x 10–3
Problem 14. If 20 ml of ethanol (density = 0.7893 gm / ml) is mixed with 40 ml of water (density = 0.9971 gm/ml) at 25°C, the final solution has density of 0.9571 gm / ml. Calculate the percentage change in total volume of mixing. Also calculate the molality of alcohol in the final solution.
Solution.
Mass of ethanol = v x d
W = 20 × 0.7893 gm = 15.786 gm
Mass of water = v × d
= 40 x 0.9971 gm = 39.884 gm
Total volume = 60 ml
Total mass = 15.786 + 39.884 = 55.67 gm
Let the volume of solution = x ml
X = mass/density = 55.67/0.9571 = 58.165 ml
Change in volume = 60 – 58.165 = 1.835 ml
% change in volume = 1.835/60 x 100
= 3.05%
Molality, m = w/m x 1000/W (in gm) = 15.786/46 x 1000/39.884
Problem 15. Calculate the mole fraction of benzene in solution containing 30% by mass in carbon tetrachloride.
Solution.
Total mass of the solution = 100 g
Mass of benzene = 30 g.
∴ Mass of carbon tetrachloride = (100 - 30)g = 70 g
Molar mass of benzene (C6H6) = (6 × 12 + 6 × 1) g mol– 1 = 78 g mol-1
∴ Number of moles of C6H6 =30/78 mol = 0.3846 mol
Molar mass of carbon tetrachloride (CCl4) = 1 × 12 + 4 × 355 = 154 g mol-1
∴ Number of moles of CCl4 = 70/154 mol = 0.4545 mol
Mole fraction of C6H6 =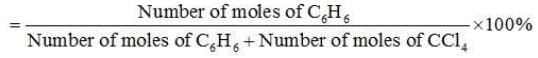

|
108 videos|286 docs|123 tests
|
FAQs on Expressing Concentration of Solutions - Chemistry Class 12 - NEET
| 1. What is mass percentage and how is it calculated? |  |
| 2. How is volume percentage defined and when is it used? |  |
| 3. What does parts per million (ppm) represent in solution concentration? |  |
| 4. What is formal concentration and how is it different from molarity? |  |
| 5. How do you calculate the dilution of a solution using the dilution formula? |  |

|
Explore Courses for NEET exam
|

|
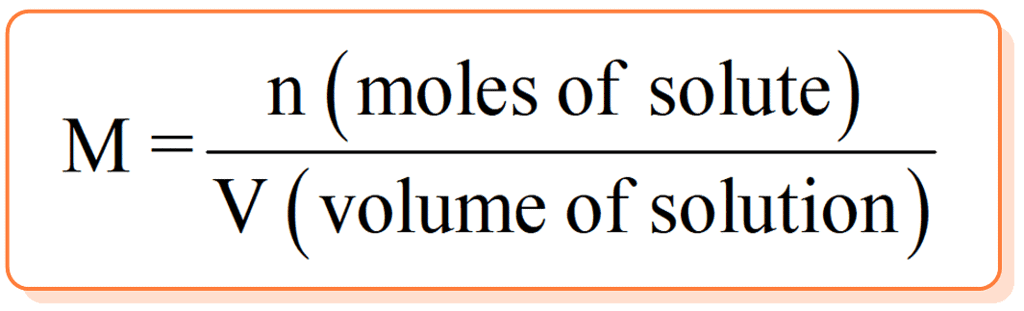 w = Mass of solute in grams
w = Mass of solute in grams
















