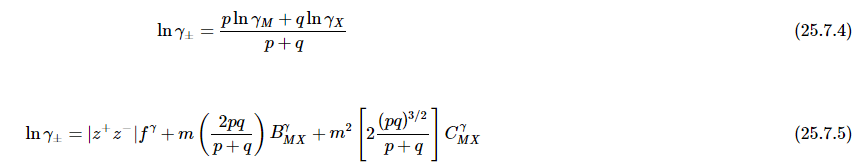Extending Debye-Hückel Theory to Higher Concentrations | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| Debye–Hückel Limiting Law |

|
| Extended Debye-Hückel Equation |

|
| Davis Equation |

|
| Pitzer Equations |

|
| Specific ion interaction theory |

|
Debye–Hückel Limiting Law
The equation for log γ± predicted from Debye–Hückel limiting law is:
It gives satisfactory agreement with experimental measurements for low electrolyte concentrations, typically less than 10−3mol/L. Deviations from the theory occur at higher concentrations and with electrolytes that produce ions of higher charges, particularly asymmetrical electrolytes. These deviations occur because the model is oversimplified, so there is little to be gained by making small adjustments to the model. Instead, we must challenge the individual assumptions of the model:
- Ions do not interact with each other. Ion association may take place, particularly with ions of higher charge. This was followed up in detail by Niels Bjerrum. The Bjerrum length is the separation at which the electrostatic interaction between two ions is comparable in magnitude to kT.
- Complete dissociation. A weak electrolyte is one that is not fully dissociated. As such it has a dissociation constant. The dissociation constant can be used to calculate the extent of dissociation and hence, make the necessary correction needed to calculate activity coefficients.
- Ions are spherical point charges that cannot be polarizable. Ions, as all other atoms and molecules, have a finite size. Many ions, such as the nitrate ion NO−3, are not spherical. Polyatomic ions are polarizable.
- The solvent composition does not matter. The solvent is not a structureless medium but is made up of molecules. The water molecules in aqueous solution are both dipolar and polarizable. Both cations and anions have a strong primary solvation shell and a weaker secondary solvation shell. Ion–solvent interactions are ignored in Debye–Hückel theory.
- Ionic radius is negligible. At higher concentrations, the ionic radius becomes comparable to the radius of the ionic atmosphere.
Most extensions to the Debye–Hückel theory are empirical in nature. They usually allow the Debye–Hückel equation to be followed at low concentration and add further terms in some power of the ionic strength to fit experimental observations. Several approaches have been proposed to extend the validity of the Debye–Hückel theory.
Extended Debye-Hückel Equation
One such approach is the Extended Debye-Hückel Equation:
where γ is the activity coefficient, z is the integer charge of the ion μ is the ionic strength of the aqueous solution, and a , is the size or effective diameter of the ion in angstrom. The effective hydrated radius of the ion, a is the radius of the ion and its closely bound water molecules. Large ions and less highly charged ions bind water less tightly and have smaller hydrated radii than smaller, more highly charged ions. Typical values are 3 Å for ions such as H+,Cl-,CN-, and HCOO-. The effective diameter for the hydronium ion is 9 Å. \ (A\) and B are constants with values of respectively 0.5085 and 0.3281 at 25°C in water. Other approaches include the Davies equation, Pitzer equations and specific ion interaction theory.
Davis Equation
- The Davies equation is an empirical extension of Debye–Hückel theory which can be used to calculate activity coefficients of electrolyte solutions at relatively high concentrations at 25 °C. The equation, originally published in 1938, was refined by fitting to experimental data. The final form of the equation gives the mean molal activity coefficient f± of an electrolyte that dissociates into ions having charges z1 and z2 as a function of ionic strength I:

- The second term, 0.30 I , goes to zero as the ionic strength goes to zero, so the equation reduces to the Debye–Hückel equation at low concentration. However, as concentration increases, the second term becomes increasingly important, so the Davies equation can be used for solutions too concentrated to allow the use of the Debye–Hückel equation. For 1:1 electrolytes the difference between measured values and those calculated with this equation is about 2% of the value for 0.1 M solutions. The calculations become less precise for electrolytes that dissociate into ions with higher charges. Further discrepancies will arise if there is association between the ions, with the formation of ion pairs, such as Mg2+SO2−4.
Plot of activity coefficients calculated using the Davies equation.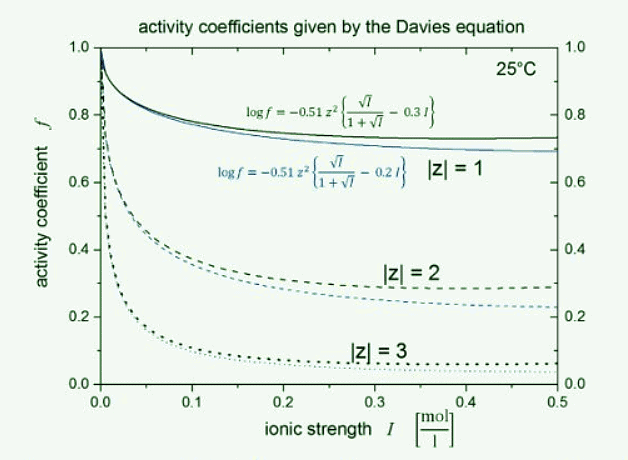
Figure 25.7.1: Semi-log plot of activity coefficients calculated using the Davies equation.
Pitzer Equations
- Pitzer equations are important for the understanding of the behaviour of ions dissolved in natural waters such as rivers, lakes and sea-water. They were first described by physical chemist Kenneth Pitzer. The parameters of the Pitzer equations are linear combinations of parameters, of a virial expansion of the excess Gibbs free energy, which characterize interactions amongst ions and solvent. The derivation is thermodynamically rigorous at a given level of expansion. The parameters may be derived from various experimental data such as the osmotic coefficient, mixed ion activity coefficients, and salt solubility. They can be used to calculate mixed ion activity coefficients and water activities in solutions of high ionic strength for which the Debye–Hückel theory is no longer adequate.
An expression is obtained for the mean activity coefficient.
- These equations were applied to an extensive range of experimental data at 25 °C with excellent agreement to about 6 mol kg−1 for various types of electrolyte. The treatment can be extended to mixed electrolytes and to include association equilibria. Values for the parameters β(0), β(1) and C for inorganic and organic acids, bases and salts have been tabulated. Temperature and pressure variation is also discussed.
Specific ion interaction theory
- Specific ion Interaction Theory (SIT theory) is a theory used to estimate single-ion activity coefficients in electrolyte solutions at relatively high concentrations. It does so by taking into consideration interaction coefficients between the various ions present in solution. Interaction coefficients are determined from equilibrium constant values obtained with solutions at various ionic strengths. The determination of SIT interaction coefficients also yields the value of the equilibrium constant at infinite dilution.
- The activity coefficient of the jth ion in solution is written as γj when concentrations are on the molal concentration scale and as yj when concentrations are on the molar concentration scale. (The molality scale is preferred in thermodynamics because molal concentrations are independent of temperature). The basic idea of SIT theory is that the activity coefficient can be expressed as

- where z is the electrical charge on the ion, I is the ionic strength, ε and b are interaction coefficients and m are concentrations. The summation extends over the other ions present in solution, which includes the ions produced by the background electrolyte. The first term in these expressions comes from Debye-Hückel theory. The second term shows how the contributions from "interaction" are dependent on concentration. Thus, the interaction coefficients are used as corrections to Debye-Hückel theory when concentrations are higher than the region of validity of that theory.

|
Explore Courses for UPSC exam
|

|