Faraday's Law of Electromagnetic Induction & Lenz's Law | Physics Class 12 - NEET PDF Download
| Table of contents |

|
| Magnetic Flux |

|
| Faraday's Law of Electromagnetic Induction |

|
| Lenz's Law |

|
| Calculation of Induced EMF |

|
Magnetic Flux
Consider a closed curve enclosing an area A. Let there be a uniform magnetic field B in that region. The magnetic flux through the area A is given by
ϕ=BAcosθ
where θ is the angle which the vector B makes with the normal to the surface. If B is perpendicular to A, then the flux through the closed area A is zero. The SI unit of magnetic flux is weber (Wb).
Notes :
Area vector is perpendicular to the surface
For open surface choose one direction as the area vector direction and stick to it for the whole problem.
For closed surfaces outward normal is taken as area vector direction
Flux is basically count of number of lines crossing a surface
Because magnetic field lines exists in closed loop.
Faraday's Law of Electromagnetic Induction
Whenever the flux of the magnetic field through the area bounded by a closed conducting loop changes, an electromotive force (emf) is produced in the loop. The emf (ε) is given by:
ε=−dΦB/dt
where ΦB is the magnetic flux through the area. The negative sign indicates the direction of the induced emf, which opposes the change in magnetic flux (Lenz's Law).
The magnetic flux (ΦB) through the area is defined as:
ΦB=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength
- A is the area bounded by the loop
- θ is the angle between the magnetic field and the normal to the loop's surface
The emf so produced drives an electric current (I) through the loop. If the resistance of the loop is R, then the current is given by:
Substituting the expression for emf, we get:
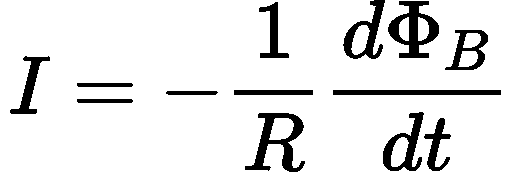
This is Faraday's law of electromagnetic induction, combined with Ohm's law, showing how the induced emf leads to an electric current in the loop
Ex. Acoil is placed in a constant magnetic field. The magnetic field is parallel to the plane of the coil as shown in figure. Find the emf induced in the coil.
Sol. f = 0 (always) since area is perpendicular to magnetic field.
Therefore, emf = 0
Ex. Find the emf induced in the coil shown in figure. The magnetic field is perpendicular to the plane of the coil and is constant.
Sol. f = BA (always) = const.
Therefore, emf = 0
Lenz's Law
The effect of the induced emf is such as to oppose the change in flux that produces it.
(a) (c) (b) (d)
In figure (a & b) as the magnet approaches the loop, the flux through the loop increases. The induced current sets up an induced magnetic field Bind whose flux opposes this change. The direction of Bind is opposite to that of the external field Bext due to the magnet.
In figure (c & d) the flux through the loop decreases as the magnet moves away from the loop. The flux due to the induced magnetic field tries to maintain the flux through the loop. The direction of Bind is the same as that of Bext due to the magnet.
Lenz's law is closely related to the law of conservation of energy and is actually a consequence of this general law of nature. As the north pole of the magnet moves towards the loop, an induced current is produced. This opposes the motion of the N-pole of the bar magnet. Thus, in order to move the magnet toward the loop with a constant velocity, an external force must be applied. The work done by this external force gets transformed into electric energy, which induces current in the loop.
There is another alternative way to find the direction of the current inside the loop, which is described below.
The figure shows a conducting loop placed near a long, straight wire carrying a current i as shown. If the current increases continuously, then there will be an emf induced inside the loop. Due to this induced emf, an electric current is induced. To determine the direction of the current inside the loop, we put an arrow as shown. The right-hand thumb rule shows that the normal to the loop is going into the plane. Again, the same rule shows that the magnetic field at the site of the loop is also going into the plane of the diagram.
Thus B and dA are in the same direction. Therefore, is positive if i increases, the magnitude of flux ϕ increases. Since magnetic flux ϕ is positive and its magnitude increases, dϕ/dt is positive. Thus ϵ is negative, and hence the current is negative. Thus the current induced is opposite to that of the arrow.
Brain Teaser
Two identical coaxial circular loops carry equal currents circulating in the same direction. What will happen to the current in each loop if the loops approach each other ?
Ex. Find the direction of induced current in the coil shown in figure. Magnetic field is perpendicular to the plane of coil and it is increasing with time.
Sol. Inward flux is increasing with time. To oppose it outward magnetic field should be induced. Hence current will flow in anticlockwise.
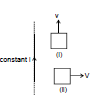
Ex. Figure shows a long current carrying wire and two rectangular loops moving with velocity v.
Find the direction of current in each loop.
Sol. In loop (i) no emf will be induced because there is no flux change.
In loop (ii) emf will be induced because the coil is moving in a region of decreasing magnetic field inward in direction. Therefore to oppose the flux decrease in inward direction, current will be induced such that its magnetic field will be inwards. For this direction of current should be clockwise.
Calculation of Induced EMF
As we know that magnetic flux (φ) linked with a closed conducting loop = BA cos θ where B is the strength of the magnetic field, A is the magnitude of the area vector and θ is the angle between magnetic field vector and area vector.
Hence flux will be affected by change in any of them.
By changing the magnetic field
Ex. Figure shows a coil placed in decreasing magnetic field applied perpendicular to the plane of coil. The magnetic field is decreasing at a rate of 10 T/s. Find out current in magnitude and direction
Sol. 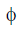 = B.A
= B.A
emf = A. = 2 × 10 = 20 v
Therefore, i = 20/5 = 4 amp. From lenz's law direction of current will be anticlockwise.
Ex The magnetic flux (φ2) in a closed circuit of resistance 20 W varies with time (t) according to the equation f = 7t2 - 4t where f is in weber and t is in seconds. The magnitude of the induced current at t = 0.25 s is
(A) 25 mA (B) 0.025 mA (C) 47 mA (D) 175 mA
Sol. φ = 7t2 - 4t
⇒ Induced emf :
⇒ Induced current :
(at t = 0.25 s)
Therefore, (A)
Ex Consider a long infinite wire carrying a time varying current i = kt (k > 0). A circular loop of radius a and resistance R is placed with its centre at a distance d from the wire (a < < d). Find out the induced current in the loop?
Sol. Since current in the wire is continuously increasing therefore we conclude that magnetic field due to this wire in the region is also increasing.
Magnetic field B due to wire going into and perpendicular to the plane of the paper
Flux through the circular loop,
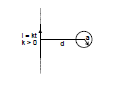
Induced e.m.f. in the loop
Induced current in the loop
Direction of induced current in the loop is anticlockwise.
Ex. Two concentric coplanar circular loops have diameters 20 cm and 2 m and resistance of unit length of the wire = 10-4 W/m. A time -dependent voltage V =(4 + 2.5 t) volts is applied to the larger as shown. The current in the smaller loop is
Sol. r1 = 1.0 m, r2 = 10-1 m
Resistance of outer loop = 2p × 10-4 ?
Resistance of inner loop = 0.2p × 10-4 ?
Current in outer loop
or
Magnetic field produced at the common centre (see figure)
or
Hence, flux linked with the inner loop,
Hence, the e.m.f. induced in smaller loop =
The negative sign indicates that the induced e.m.f. (or current) is opposite to applied e.m.f. (or current)
Hence, the current induced in the inner (smaller) loop is
Ex. A rectangular wire frame of length 0.2 m, is located at a distance of 5 × 10-2 m from a long straight wire carrying a current of 10 A as shown in the figure. The width of the frame = 0.05 m. The wire is in the plane of the rectangle. Find the magnetic flux through the rectangular circuit. If the current decays uniformly to 0 in 0.2 s, find the emf induced in the circuit.
Sol. A current, i = 10 A is flowing in the long straight wire. Consider a small rectangular strip (in the rectangular wire frame) of width dx at a distance x from the straight wire.
The magnetic flux at the location of the strip,
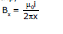
The flux linked with the infinitesimally small rectangular strip
= Bx × Area of the strip = d x =
x = l dx
where l is the length of the rectangular wire circuit
= 2 × 10-1 m
or d x = (m0 il/2p) (dx/x)
x = (m0 il/2p) (dx/x)
Hence, the total magnetic flux linked with the rectangular frame
=
or
Substituting values, we get
 = 2 × 10-7 × 10 × 2 × 10-1 × loge2
= 2 × 10-7 × 10 × 2 × 10-1 × loge2
= 2.772 × 10-7 Wb
Induced e.m.f.
= 1.386 ×10-6 V = 1.386 mV
Ex. Figure shows a wire frame PQSTXYZ placed in a time varying magnetic field given as B = bt, where b is a positive constant. Resistance per unit length of the wire is l. Find the current induced in the wire and draw its electrical equivalent diagram.
Sol. Induced emf in part PQST = b a2 (in anticlockwise direction, from Lenz's Law) Similarly induced emf in part TXYZ = b b2 (in anticlockwise direction, from Lenz's Law)
Total resistance of the part PQST = l4a
Total resistance of the part PQST = l4b.
The equivalent circuit it is shown in the diagram.
writing KVL along the current flow
i =
Brain Teaser :
A copper ring is held horizontally and a bar magnet is dropped through the ring with its length along the axis of the ring. Will the acceleration of the falling magnet be equal to, greater than or lesser than the acceleration due to gravity ?
By Changing the Area
Solved Examples :
Ex. A space is divided by the line AD into two regions. Region I is field free and the region II has a uniform magnetic field B directed into the paper. ACD is a semicircular conducting loop of radius r with centre at O, the plane of the loop being in the plane of the paper. The loop is now made to rotate with a constant angular velocity w about an axis passing through O, and perpendicular to the plane of the paper in the clockwise direction. The effective resistance of the loop is R.
(a) Obtain an expression for the magnitude of the induced current in the loop.
(b) Show the direction of the current when the loop is entering into the region II.
(c) Plot a graph between the induced emf and the time of rotation for two periods of rotation.
Sol. (a) As in time t, the arc swept by the loop in the field, i.e., region II.
A =
So the flux linked with the rotating loop at time t,
f = BA =
and hence the induced emf in the loop,
e = - = -
= constant.
And as the resistance of the loop is R, the induced current in it,
(b) When the loop is entering the region II, i.e., the field figure (b), the inward flux linked with it will increase, so in accordance with Lenz's law an anticlockwise current will be induced in it.
(c) Taking induced emf to the negative when flux linked with the loop is increasing and positive when decreasing, the emf versus time graph will be, as shown in figure (c)
Ex. Two parallel, long, straight conductors lie on a smooth plane surface. Two other parallel conductors rest on them at right angles so as to form a square of side a initially. A uniform magnetic field B exists at right angles to the plane containing the conductors. Now they start moving out with a constant velocity (v). (a) Will the induced emf be time dependent? (b) Will the current be time dependent?
Sol. (a) Yes, φ (instantaneous flux) = B (a + 2vt)2
Therefore, e = = 4Bv(a + 2vt)
(b) No,
(instantaneous current) i =
Now R = 4(a + 2vt)r where r = resistance per unit length
Therefore, i = =
(a constant)
The current will be time independent.
|
74 videos|314 docs|88 tests
|
FAQs on Faraday's Law of Electromagnetic Induction & Lenz's Law - Physics Class 12 - NEET
| 1. What is magnetic flux? |  |
| 2. What is Faraday's Law of Electromagnetic Induction? |  |
| 3. What is Lenz's Law? |  |
| 4. How are Faraday's Law of Electromagnetic Induction and Lenz's Law related? |  |
| 5. How can Faraday's Law of Electromagnetic Induction and Lenz's Law be applied in real-life scenarios? |  |















