JEE Advanced (Fill in the Blanks): Functions | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q. 1. The values of f(x) 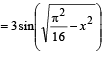 lie in the interval
lie in the interval
Ans. 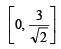
Solution. For the given function to be defined
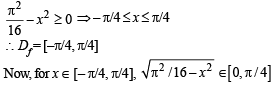
and sine function increases on [0, π/4]
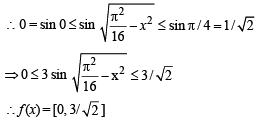
Q. 2. For the function
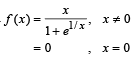
the derivative from the right, f '(0+) = ......................., and the derivative from the left, f '(0–) = ...............
Ans. 0, 1
Solution.

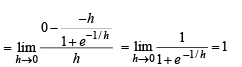
Thus f ' (0+) = 0 and f ' (0–) = 1
Q. 3. The domain of the function 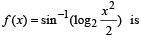 given by .................
given by .................
Ans. [–2, –1] ∪ [1, 2]
Solution. To find domain of function 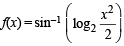
For f (x) to be defined we should have 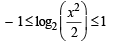
NOTE THIS STEP :
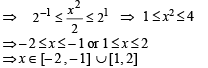
Q. 4. Let A be a set of n distinct elements. Then the total number of distinct functions from A to A is ................. and out of these ................. are onto functions.
Ans. nn, n!
Solution. Set A has n distinct elements. Then to define a function from A to A, we need to associate each element of set A to any one the n elements of set A. So total number of functions from set A to set A is equal to the number of ways of doing n jobs where each job can be done in n ways. The total number such ways is n × n × n × .... × n (n - times).
Hence the total number of functions from A to A is nn.
Now for an onto function from A to A, we need to associate each element of A to one and only one element of A. So total number of onto functions from set A to A is equal to number of ways of arranging n elements in range (set A) keeping n elements fixed in domain (set A). n elements can be arranged in n! ways.
Hence, the total number of functions from A to A is n!.
Q. 5. If 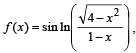 , then domain of f(x) is .... and its range is .................
, then domain of f(x) is .... and its range is .................
Ans. (-2, 1), [-1, 1]
Solution. The given function is,
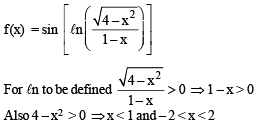
Combining these two inequalities, we get x ∈ (– 2, 1)
∴ Domain of f is (– 2, 1)
Also sin q always lies in [– 1, 1].
∴ Range of f is [– 1, 1]
Q. 6. There are exactly two distinct linear functions, ................., and ........... which map [– 1, 1] onto [0, 2].
Ans. x + 1 and - x+ 1
Solution. KEY CONCEPT : Every linear function is either strictly increasing or strictly decreasing. If f (x) = ax + b, Df = [p, q], Rf = [m, n]
Then f (p) = m and f (q) = n, if f (x) is strictly increasing and f (p) = n, f (q) = m, If f (x) is strictly decreasing function.
Let f (x) = ax + b be the linear function which maps [–1, 1] onto [0, 2]. then f (–1) = 0 and f (1) = 2 or f (–1) = 2 and f (1) = 0
Depending upon f (x) is increasing or decreasing respectively.
⇒ – a + b = 0 and a + b = 2 ....(1)
or – a + b = 2 and a + b = 0 ....(2)
Solving (1), we get a = 1, b = 1.
Solving (2), we get a = – 1, b = 1
Thus there are only two functions i.e., x + 1 and – x + 1.
Q. 7. If f is an even function defined on the interval (-5, 5), then four real values of x satisfying the equation 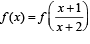
are ................., ................., ................., and ...........
Ans. 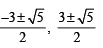
Solution. Given that 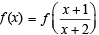 and f is an even function
and f is an even function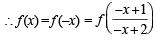
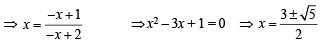
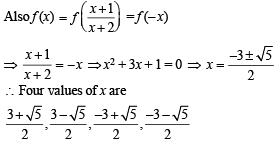
Q. 8. If f(x) = sin2 x + 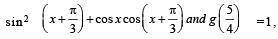 then (gof) (x) = .................
then (gof) (x) = .................
Ans. 1
Solution.
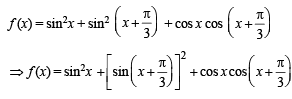
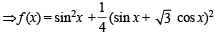
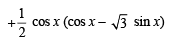
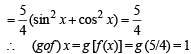
|
446 docs|929 tests
|
















