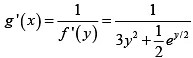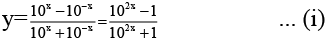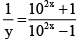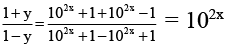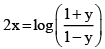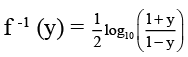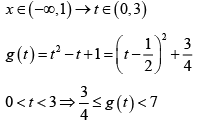Integer Answer Type Questions for JEE: Sets, Relation & Functions | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. If f is a function such that f(0) = 2, f(1) = 3 and f(x + 2) = 2f(x) – f(x + 1) for every real x then f(5) is
Ans. 13
For x = 0, f(2) = 2f(0) – f(1) = 2 × 2 – 3 = 1,
for x = 1, f(3) = 2f(1) – f(2) = 6 – 1 = 5,
for x = 2, f(4) = 2f(2) – f(3) = 2 × 1 – 5 = -3,
for x = 3, f(5) = 2f(3) – f(4) = 2×5 – (-3)= 13.
Q.2. If f''(x) = - f(x) and g(x) = f'(x) and F(x) =  and given that F(5) = 5, then F(10) is equal to
and given that F(5) = 5, then F(10) is equal to
Ans. 5
f''(x) = -f(x) and f'(x) = g(x)
⇒ f''(x) . f'(x) + f(x) . f'(x) = 0
⇒ f(x)2 + (f'(x))2 = c
⇒ (f(x)2 + (g(x))2 = c
⇒ F(x) = c
⇒ F(10) = 5.
Q.3. If f (x + y) = f(x) + f(y) - xy - 1 for all x, y, and f(1) = 1 then the number of Solutions of f(n) = n, n ∈ N, is
Ans. 1
Putting y = 1, f (x + 1) = f (x) + f (1) - x - 1 = f (x) - x.
∴ f (n + 1) = f (n) - n < f (n).
So, f (n) < f (n - 1) < f (n - 2) < … < f (1) = 1
∴ f (n) = n holds for n = 1 only.
Q.4. The period of the function f(x) = 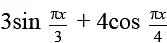 is
is
Ans. 24
The period of sinπx/3 is 2π/π/3, i.e. 6. The period of cosπx/4 is, i.e., 8.
LCM of 6 and 8 is 24. So, the period of f(x) = 24.
Q.5. If the period of the function f(x) = 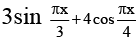 is 3k then k, is
is 3k then k, is
k, is
Ans. 8
has period 6
4cos πx/4 has period 8
Net period 24 3k = 24
⇒ k = 8.
Q.6. If the function f (x) = 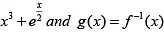 , then the value of g '(1) is
, then the value of g '(1) is
Ans. 2
Let y = g ( x)= f -1 ( x) . Then x = 1
⇒ y = 0(sin ce f (0) = 1)
∴ g ' (1)= 2
Q.7. The inverse of the function y = 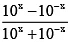 is
is 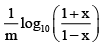 , m ≠ 0, then the value of m is
, m ≠ 0, then the value of m is
Ans. 2
The function is one-one for if y(x1) = y(x2)
then⇒ x1 = x2
We have,
⇒
⇒
∴ m = 2 .
Q.8. If log2x + logx2 = 5/2 = log2y + logy2 and x ≠ y, then the value of x + y - √2 is
Ans. 4
log2x + logx2 = 5/2 = log2y + logy2
⇒where t = log2x,, s = log2y
⇒ t = 2, 1/2 & s = 2, 1/2 (as t ≠ s, x ≠ y)
∴ t = 2 and s = 1/2 or t = 1/2 and s = 3
∴ log2X = 2 and log2y = 1/2
x = 4 and y = √2
x + y - √2 = 4 + √2 - √2 = 4.
Q.9. The number of elements in the range of the function f : (-∞,1) → R , defined by f (x) = [9x - 3x -+ 1] , where [.] is the greatest integer function, is
Ans. 7
Put 3x = t . Then 3x → 0 as x → -∞ and 3x → 3 as x → 1
No of elements in the range of [g(t)] is 7.
Q.10. Let A and B be finite sets containing respectively 3 and 2 elements. Find the number of functions that can be defined from A to B
Ans. 8
Since each of 3 elements of A can associated to an element of B in 2 ways.
Therefore all the 3 elements can be associated with elements of B in 23 ways.
|
446 docs|930 tests
|