Financial Derivatives: Option, Futures and swap | Management Optional Notes for UPSC PDF Download
| Table of contents |

|
| Forward Contracts |

|
| Futures Contract |

|
| Options Position |

|
| Swaps |

|
Forward Contracts
- Forward contracts, often referred to as forwards, have thrived for centuries across numerous nations, India among them. They stand out as the most basic form of derivatives. Essentially, a forward contract is a tailor-made agreement between two parties, stipulating settlement on a specified future date at a price agreed upon today.
- A forward contract is a bilateral agreement set to be executed in the future based on terms negotiated today. One party, known as the long position, commits to buying the underlying asset at an agreed-upon price on a specified future date, while the other party, the short position, agrees to sell the asset at the same terms and time. For instance, two parties might agree to exchange 100 shares of Reliance at Rs 850 per share in two months. However, such contracts carry the risk of default, where one party may choose not to honor the agreement due to favorable market conditions. This mutual default risk exposes both parties to potential losses. Forward contracts, commonly utilized in India's foreign exchange market to mitigate currency risk, offer flexibility in customizing terms like price, quantity, and delivery time. However, their customized nature often results in poor liquidity and credit risk due to the potential for default, as illustrated above.
- Additionally, let's examine the payoff calculation of a forward contract using an example where two parties agree to exchange 500,000 barrels of crude oil at a price of US $ 42.08 per barrel in three months. The contract's parameters include the underlier (oil), notional amount (500,000 barrels), delivery price (US $ 42 per barrel), and settlement date. The party receiving the underlier is considered long, while the other party is short. At settlement, the forward's market value is determined by the difference between the spot price and the delivery price, multiplied by the notional amount. This formula indicates that forwards yield linear payoffs. Furthermore, forward contracts may be cash-settled, eliminating the physical exchange of assets. In such cases, a single payment is made based on the market value of the forward at settlement. Forward prices, quoted as delivery prices, fluctuate based on market conditions and often diverge from spot prices due to factors like time value of money and market expectations. A graph displaying forward prices for various maturities is referred to as a forward curve.
Futures Contract
- A futures contract refers to a legally binding arrangement to buy or sell the underlying asset at a specified future date. These contracts are standardized concerning quantity, quality (for commodities), delivery time, and place for settlement on any future date. They have an expiration date, after which settlement can occur through either delivery of the asset or cash. Unlike forward contracts, futures are typically traded on exchanges, making them more liquid.
- In futures markets, a clearing corporation or house acts as the counterparty for all trades or provides unconditional guarantees for settlement, ensuring financial integrity. This differs from forward markets where liquidity and settlement issues may arise. For example, if A and B enter a contract to trade shares of Reliance on an exchange with a clearing house guaranteeing settlement, it is considered a futures contract.
Key Differences between Futures and Forwards:
- Standardization: Futures contracts are standardized instruments traded on exchanges, whereas forwards are customizable contracts traded over the counter. Futures contracts are limited to specific contracts supported by the exchange, while forwards can be tailored to various underliers and settlement dates, with parties determining the notional amount and settlement method.
- Risk Exposure: Forwards involve both market and credit risk, as a counterparty may fail to fulfill the contract. In contrast, futures contracts only carry market risk due to daily margin payments exchanged between counterparties, effectively resetting the contract's market value each trading day and mitigating credit risk.
- Price Discrepancies: The daily margin payments associated with futures contracts can impact prices, leading to divergences from forward prices. This phenomenon can skew futures prices due to the constant adjustments made through margining.
Given the above, it can be asserted that when a forward contract is standardized and traded on an exchange, it transforms into a futures contract. Therefore, all futures contracts are essentially standardized forward contracts. Both forwards and futures serve the same purpose, but futures execute more effectively due to transparency and robust risk management measures. Settlement for futures contracts can occur through physical delivery of assets or solely in cash, with clear specifications outlined in the contract by the exchanges.
- Futures transactions are facilitated through brokerage firms holding a seat on the exchange trading the specific contract. These transactions involve two parties, each transacting with the exchange's clearinghouse. For instance, if Party A and Party B trade five May natural gas futures at US$ 3.24, Party A is considered long and Party B short. Legally, Party A is long five May natural gas futures at US$ 3.24 with the exchange's clearinghouse as the counterparty, while the clearinghouse is long the same futures with Party B as the counterparty. Thus, Party A and B have no direct legal obligations to each other, with their obligations solely directed towards the clearinghouse, which effectively manages market risks through offsetting positions.
- In a futures transaction negotiated between two parties via their respective brokers, the legal structure involves two contracts—one between each party and the exchange's clearinghouse. This arrangement mitigates credit risk between the parties, as their credit exposure is solely to the clearinghouse, substantially reduced through margining processes. Before trading futures, brokers collect an initial margin deposit from clients, which is determined by exchange-set formulas and represents a fraction of the futures' market value. Daily margining processes ensure ongoing settlement of obligations, effectively eliminating credit risk as profits or losses are realized and transferred between parties and the clearinghouse.
- Futures contracts settle daily through mark-to-market processes, unlike forwards where obligations are fulfilled at maturity. Various types of futures exist, such as Index Futures and Stock Futures, each based on specific underlying assets. For example, futures contracts on indices like NIFTY and BSE-30 are cash-settled, deriving their value from the underlying index. Stock futures, on the other hand, involve buying or selling a specific stock at a future date, with single stock futures also being cash-settled.
- Options Contracts are a form of Derivatives Contract granting the buyer/holder the right (but not the obligation) to buy/sell the underlying asset at a predetermined price within or by the end of a specified period. The buyer/holder pays a premium to the seller/writer for this right, and the seller/writer is obligated to fulfill the terms of the contract upon exercise by the buyer/holder. Under the Securities Contracts (Regulation) Act, 1956, options on securities encompass various contracts for future purchase or sale of securities, including calls, puts, or combinations thereof.
- A Call option provides the right to buy, while a Put option allows selling. Options can be categorized as American, exercisable at any time before expiry, or European, exercisable only on expiry. The predetermined price for exercising the option is known as the Strike or Exercise price. Unlike forward or futures contracts, options entail a cost to acquire. For instance, a three-month European option on Brent oil with a strike price of US $45 per barrel grants the holder the right to sell 100,000 barrels at that price.
- In a practical example, if Mr. A wants to buy a television worth Rs. 12,000 but lacks the full payment, he may offer a partial amount to reserve the TV for a specified period. This resembles a forward contract, where non-fulfillment leads to forfeiture. Alternatively, Mr. A could pay a smaller fee to reserve the TV with the option to buy it later, similar to an option contract. If Mr. A finds a better deal elsewhere, he may choose to let the option expire, losing the reservation fee.
- American options allow exercise at any time before expiry, with the exchange randomly assigning exercise requests to sellers who must settle within a set timeframe. Options contracts, like futures, can be settled by delivery of the underlying asset or cash. However, cash settlement in options involves paying/receiving the difference between the strike price and the asset's price at expiry or exercise.
- Index options contracts, based on an index, grant the buyer the right (but not obligation) to buy/sell the underlying index at expiry. They are generally European-style options, exercisable only on expiry. Investment strategies with index options mirror those of individual stock options, with investors utilizing calls for anticipated market rises and puts for expected declines. Index options offer advantages of lower cost and greater efficiency compared to options on individual stocks due to diversification benefits inherent in index portfolios.
- Initially, futures and options were exclusively allowed on S&P Nifty and BSE Sensex. Later, sectoral indices also became eligible for derivatives trading, provided they met certain criteria. Derivative contracts could be permitted on an index if at least 80% of its constituents were individually eligible for derivatives trading. Additionally, no single ineligible stock within the index could have a weightage exceeding 5%. The index needed to maintain eligibility criteria even after derivatives trading commenced. If an index failed to meet the criteria for three consecutive months, derivative contracts on that index would be ceased.
- Index futures and index option contracts are cash settled upon expiry as indices cannot be physically delivered. In options markets, the exercise price refers to the price at which the option holder can buy or sell the underlying asset. A call option is considered "in the money" if the current asset price exceeds the exercise price, and "out of the money" if it is lower. Near-the-money call options have exercise prices slightly above the current market price. The premium is the price paid by the buyer to the seller of the option, whether a put or a call. A call option written against owned assets by the writer is termed a covered option, while one written without owning the asset is called a naked option.
- The world options markets offer a diverse range of options, including simple ones like commodity options, stock options, bond options, currency options, and stock index options. There are also compound options such as swaptions, flortions, and captions, as well as synthetic options that combine options and futures.
Options Position
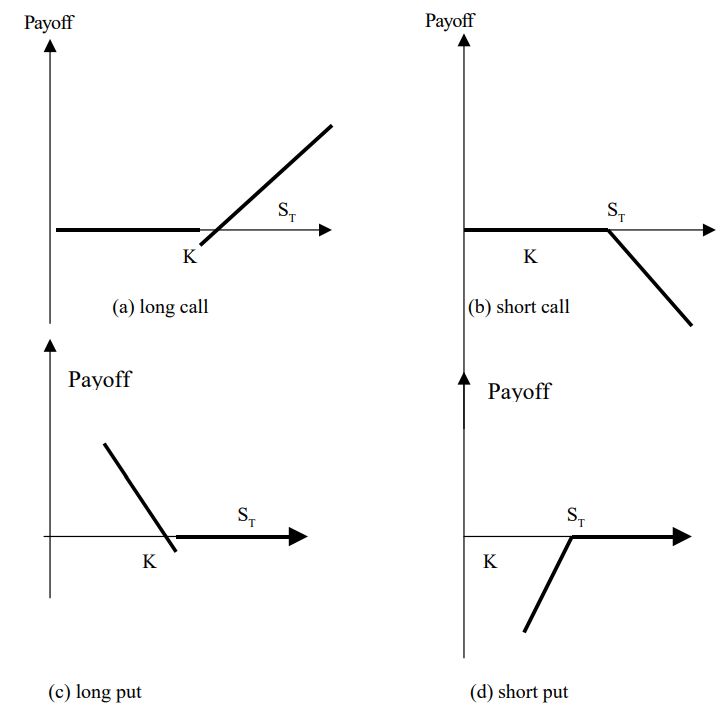
Every option contract involves two parties: the investor who holds a long position (i.e., purchased the option) and the investor who holds a short position (i.e., sold or wrote the option). The writer of an option receives an upfront cash payment but may face potential liabilities later. The profit or loss for the writer is the opposite of that for the option purchaser. There are four types of option positions:
- Long position in a call option
- Long position in a put option
- Short position in a call option
- Short position in a put option
It is often helpful to describe European option positions based on the terminal value or payoff to the investor at maturity, excluding the initial cost of the option from the calculation. If K represents the strike price and ST is the final price of the underlying asset, the payoff from a long position in a European call option is expressed as:
- max(ST - K, 0)
The option will be exercised if ST> K and not be exercised if ST d” K. The payoff to the holder of a short position in the European call option is
– max (ST – K, 0) = min (K – ST, 0).
The payoff to the holder of a long position in a European put potion is max (K – ST, 0) = min (ST – K, 0)
The payoffs from a short position in a European put option is
– max (K – ST, 0) = min (ST – K, 0)
Payoffs from positions in European options
Swaps
- A swap denotes an agreement between two parties to exchange assets, financial obligations, or a series of cash flows over a specified period at predetermined intervals. Swaps encompass both spot and forward transactions within a single agreement and are typically tailored to the parties' specific needs. Corporations, banks, and individual investors increasingly utilize swaps to facilitate intricate and innovative financing structures aimed at reducing borrowing costs and managing interest rate and foreign currency exposure more effectively.
- While swaps serve diverse purposes, ranging from hedging to speculation, their primary function is to alter the nature of an asset or liability without requiring its liquidation. For instance, an investor realizing returns from equity investments can swap those returns into less volatile fixed income cash flows without selling the equities. Similarly, a corporation carrying floating-rate debt can convert it into fixed-rate obligations without the need for debt retirement and reissuance.
- Among various types of swaps, the most prevalent is the "plain vanilla" interest rate swap, where one party agrees to pay fixed-rate cash flows on a notional principal while receiving floating-rate cash flows on the same principal for a specified period. Interest rate swaps and currency swaps are the most commonly used types among various swap arrangements.
- An interest rate swap involves an exchange of interest payment streams between two parties based on a notional principal amount, with maturities typically ranging from under a year to over 15 years. Currency swaps entail exchanging foreign currency in the spot market while simultaneously agreeing to reverse the transaction in the forward market at predetermined exchange rates and timing.
- For example, a company can hedge exchange rate risk by swapping rupees for dollars at a fixed or floating interest rate, thereby managing both interest rate and exchange rate risks effectively.
- In the derivative market, participants can be broadly categorized into three groups: hedgers, speculators, and arbitrageurs. Hedgers utilize forwards, futures, and options to mitigate potential risks arising from future market movements. Speculators use derivatives to speculate on the future direction of market variables, while arbitrageurs engage in simultaneous trading of two or more instruments to capitalize on price discrepancies and lock in profits.
- Put–Call parity in financial mathematics establishes a connection between the prices of a European call option and a European put option, both sharing the same strike price and expiration date. The derivation of this relationship relies solely on the absence of arbitrage opportunities in the market, without any additional assumptions.
- For example, let's examine stock options, although this concept can be extended more broadly. Consider a call option and a put option with an identical strike price (K) expiring on the same date (T) for a dividend-free share. Let S represent the unknown underlying asset value at expiration.
- If S <= K (the put is valued at K–S and the share is valued at S)
- If S >= K (the put has no value and the share is valued at S)
- Now, let's analyze two portfolios: one comprising a put option and one share, and the other consisting of a call option and K bonds, each paying 1 unit with certainty at time T.
- The first portfolio's value at time T:
- The second portfolio's value at time T:
- If the share price at time T were lower in one portfolio compared to the other at some earlier time t, an arbitrage opportunity would arise. By buying the cheaper portfolio and selling the more expensive one, one could generate riskless profit, contradicting market efficiency.
- Consequently, both portfolios must hold the same value at any time t before T, leading to the following relationship among the instruments' values at a general time t:
C(t) + K * B(t,T) = P(t) + S(t)
Where:
- C(t) represents the time-t value of the call option
- P(t) represents the time-t value of the put option
- S(t) represents the time-t value of the share
- K is the strike price
B(t,T) represents the time-t value of a bond that matures at T. For stocks paying dividends, these should be factored into B(t, T) as option prices typically do not adjust for regular dividends. Assuming a constant bond interest rate r, B(t, T) equals e(-r(T–t)). With the knowledge of any three of the call, put, bond, and stock prices, one can compute the implied fair value of the fourth instrument using the above equation.
Put-call parity suggests two key principles:
- Equality between calls and puts: Put-call parity establishes that a call option and a put option can be effectively substituted for one another in any delta-neutral portfolio. If 'd' represents the delta of the call option, then purchasing a call and simultaneously selling 'd' shares of stock is equivalent to buying a put and purchasing '1 - d' shares of stock. This equivalence between calls and puts holds significant importance in options trading strategies.
- Equality of implied volatility: In scenarios devoid of dividends or other carry costs, such as when a stock is challenging to borrow or sell short, the implied volatility of both call and put options must be identical. This principle underscores the parity of implied volatility between calls and puts in such conditions.
FAQs on Financial Derivatives: Option, Futures and swap - Management Optional Notes for UPSC
| 1. What are forward contracts? |  |
| 2. What is a futures contract? |  |
| 3. What is an options position? |  |
| 4. What are swaps in financial derivatives? |  |
| 5. What are the benefits of using financial derivatives? |  |














