First Law of Thermodynamics | Chemistry Class 11 - NEET PDF Download
| Table of contents |

|
| First Law of Thermodynamics |

|
| Mathematical Expression of First Law |

|
| Solved Numerical |

|
| Try Yourself! |

|
| Reversible Process |

|
| Irreversible Process |

|
First Law of Thermodynamics
The first law of thermodynamics states that energy can neither be created nor destroyed, although it can be transformed from one form to another. This is also known as the law of conservation of energy. The energy of an isolated system is constant.
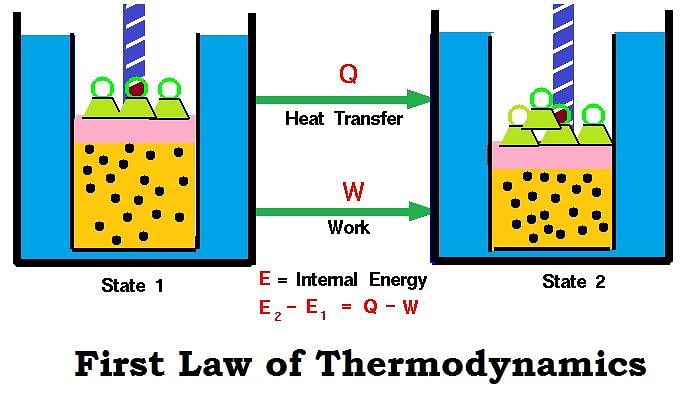
Mathematical Expression of First Law
If a closed system having U1 internal energy is supplied ‘q’ amount of heat, then internal energy of the system becomes (U1 + q).
If work (w) is done on the system, then its internal energy further increases and becomes U2.
Thus, U2 = U1 + q + w
U2 – U1 = q + w
ΔU= q + w
In case q is the heat absorbed and w is the work done by the system then:
ΔU = q + (- w)
ΔU = q - w
➤ Case 1: Let UA be the energy of a system in its state A and UB be the energy in its state B.
Suppose the system while undergoing change from state A to state B absorbs heat q from the surroundings and also performs some work (mechanical or electrical), equal to w.
- The absorption of heat by the system tends to raise the energy of the system. (q = + ve)
- The performance of work by the system, on the other hand, tends to lower the energy of the system because performance of work requires expenditure of energy. (w = -ve)
Hence, the change of internal energy, ΔU, accompanying the above process will be given by:
ΔU = q + (- w)
or
ΔE = q + (- w)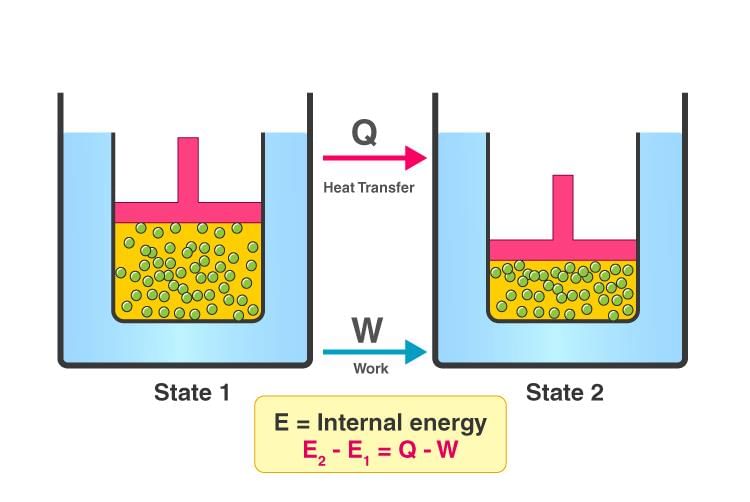 Any thermodynamic system in an equilibrium state possesses a state variable called the internal energy (E). Between any two equilibrium states, the change in internal energy is equal to the difference of the heat transfer into the system and work done by the system. ΔU = q - w
Any thermodynamic system in an equilibrium state possesses a state variable called the internal energy (E). Between any two equilibrium states, the change in internal energy is equal to the difference of the heat transfer into the system and work done by the system. ΔU = q - w
➤ Case 2: In general, if in a given process the quantity of heat transferred from the surrounding to the system is q and work done on the system is w, then the change in internal energy.
ΔU = q + w
or
ΔE = q + w
This is the mathematical statement of the first law of thermodynamics.
Conclusion: If work is done by the surroundings on the system (as during the compression of a gas), w is taken as positive so that ΔU = q + w.
If work is done by the system on the surroundings (as during the expansion of a gas), w is taken as negative so that ΔU = q - w.
Some useful conclusions drawn from the first law:
ΔE = q + w
(i) When a system undergoes a change ΔE=0, i.e. , there is no increase or decrease in the internal energy of the system. The first law of thermodynamics reduces to
0 = q + w
- q = -w
(heat absorbed from surroundings = work done by the system) - w = -q
(heat given to surroundings = work done on the system)
(ii) If no work is done, w = 0 and the first law reduces to
ΔE =q
Or
ΔU =q
i.e. , increase in internal energy of the system is equal to the heat absorbed by the system or decrease in internal energy of the system is equal to heat lost by the system.
(iii) If there is no exchange of heat between the system and surroundings, q = 0, the first law reduces to M w It shows that if work is done on the system, its internal energy will increase or if work is done by the system, its internal energy will decrease. This occurs in an adiabatic process.
(iv) In case of gaseous system, if a gas expands against the constant external pressure, P, let the volume change be !:lV. The mechanical work done by the gas is equal to -P x !:lV.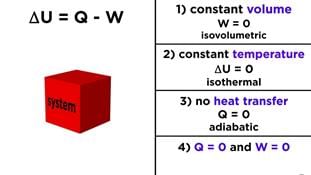
Solved Numerical
Example 1. In a certain process, 670 J of heat is absorbed by a system while 264 J of work is done on the system. What is the change in internal energy of the process?
Solution. q = + 670 J
w = + 264 (∵ work is done on the system)
We know that, ΔE = q + w = 670 + 264 = 934 J.
Example 2. If 150 J of heat is added to a system while the system does work equivalent of 255 J by expanding against in surrounding atmosphere, what is the value of ΔE for the system?
Solution. q = + 150 J
w = – 255 J (work done by a system is negative)
ΔE = q + w = + 150 + (-255) = - 105 J.
Example 3. If 500 calorie of heat energy are added to a system and the system does 350 calorie of work on the surroundings, what is the energy change of the system?
Solution. Heat absorbed, q = 500cal
Work done by the system, w = -350cal
Applying the first law of thermodynamics:
M = q + w
500+ (-350)= 150 calorie
Try Yourself!
Q.1. A 1.0 kJ of heat is added to 1.50 L of ideal gas in a cylinder at constant pressure of 1.00 atm, the volume increases to 2.30 L. Calculate ΔE for the process.
Ans. 919.2 J
Q.2. How much work is done on or by the system, if the internal energy of the system decreases by 100 J when 200 J of heat is supplied to the system.
Ans. – 300 J
Reversible Process
- A thermodynamic process (state i → state f) is said to be reversible if the process can be turned back such that both the system and the surroundings return to their original states, with no other change anywhere else in the universe.
- As we know, in reality, no such processes as reversible processes can exist, thus, the reversible processes can easily be defined as idealizations or models of real processes, on which the limits of the system or device are to be defined.
- They help us in incurring the maximum efficiency a system can provide in ideal working conditions and thus the target design that can be set.
- So, Reversible process can be defined as:
A process or change is said to be reversible, if a change is brought out in such a way that the process could, at any moment, be reversed by an infinitesimal change. A reversible process proceeds infinitely slowly by a series of equilibrium states such that system and the surroundings are always in near equilibrium with each other.
- An ideal reversible process will take infinite time to get completed.
- It is carried out infinitesimally slowly.
- Strictly speaking, there is no ideal reversible process in universe.
➤ Examples of Reversible Process
Here, we have listed a few examples of Reversible Process:
- Extension of springs.
- Slow adiabatic compression or expansion of gases.
- Electrolysis (with no resistance in the electrolyte).
- Frictionless motion of solids.
- Slow isothermal compression or expansion of gases.
To get an idea of a reversible process we can consider the following system:
An ideal gas is enclosed in a container and a massless piston is put on the gas on which a pile of sand is placed having particles of negligible mass. To carry out a reversible expansion we will slowing decrease the mass of the sand let’s say by removing the particles one by one, so the expansion of the gas will take place at infinitesimally small rate and we can always assume the system to be in thermodynamic equilibrium. So, the expansion will be of reversible type.
Irreversible Process
An irreversible process can be defined as a process in which the system and the surroundings do not return to their original condition once the process is initiated. Taking an example of an automobile engine, that has travelled a distance with the aid of fuel equal to an amount ‘x’.
During the process, the fuel burns to provide energy to the engine, converting itself into smoke and heat energy. We cannot retrieve the energy lost by the fuel and cannot get back the original form.
There are many factors due to which the irreversibility of a process occurs, namely:
- The friction that converts the energy of the fuel to heat energy.
- The unrestrained expansion of the fluid which prevents from regaining the original form of the fuel Heat transfer through a finite temperature, reverse of which is not possible as the forward process, in this case, is spontaneous.
- Mixing of two different substances which cannot be separated as the process of intermixing is again spontaneous in nature, the reverse of which is not feasible.
Thus, some processes are reversible while others are irreversible in nature depending upon their ability to return to their original state from their final state.
➤ Examples of Irreversible Processes
A few examples of Irreversible Processes are:
- Relative motion with friction
- Throttling
- Heat transfer
- Diffusion
- Electricity flow through a resistance
Processes other than reversible processes are known as irreversible processes.
 Reversible and Irreversible Process
Reversible and Irreversible Process

|
127 videos|244 docs|87 tests
|
FAQs on First Law of Thermodynamics - Chemistry Class 11 - NEET
| 1. What is the First Law of Thermodynamics? |  |
| 2. What is the mathematical expression of the First Law of Thermodynamics? |  |
| 3. Can you provide an example of a solved numerical problem related to the First Law of Thermodynamics? |  |
| 4. What is a reversible process in thermodynamics? |  |
| 5. What is an irreversible process in thermodynamics? |  |

|
Explore Courses for NEET exam
|

|




















