First-order equations (linear and nonlinear) | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download
First Order Linear Differential Equations
The differential equation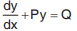 is called a linear differential equation because the dependent variables and its derivatives appear only in the first degree. Here P and Q are functions of x alone or are constants.
is called a linear differential equation because the dependent variables and its derivatives appear only in the first degree. Here P and Q are functions of x alone or are constants.Integrating Factor : e∫P dx
General solution : y (I.F.) = ∫Q I.F. dx + C

Solved Example 1: Solve 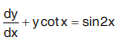
Solution: Here P = cot x
Q = sin 2x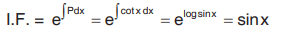
General solution is y sinx
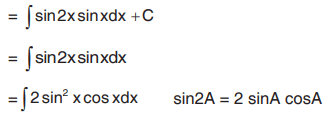
Put sin x = t
cos x dx = dt
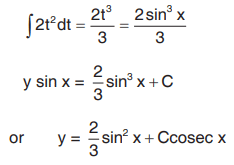
Solved Example 2: Solve: 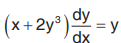
Solution: The equation is
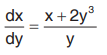

General solution is

First Order Differential Equations reducible to Linear form
An equation of the form
where P and Q are constants or functions of x alone can be reduced to linear form as follows:
Putting f(y) = v so that 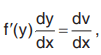 ,
,
Above equation becomes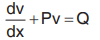
which is linear in v and x and its solution can be obtained by using working rule as for first order linear differential equation. Thus, we have I.F. = e∫P dx
Solution is 
Finally, replacing v by f(y) will give solution in terms of x and y alone.
An equation of the form 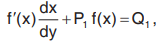 where P1 and Q1 are constants or functions of y alone can be reduced to linear form in the same way as describe above by putting f(x) = v.
where P1 and Q1 are constants or functions of y alone can be reduced to linear form in the same way as describe above by putting f(x) = v.
Bernoulli’s Equation
The equation of the form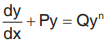 where P and Q are the functions of x alone is called Bernoulli’s equation. When n = 0 or n = 1 it is already linear. For other values of n it can be reduced to linear equation by the substitution z = y1-n. This is describe as follows: Multiplying the above equation by y-n ,
where P and Q are the functions of x alone is called Bernoulli’s equation. When n = 0 or n = 1 it is already linear. For other values of n it can be reduced to linear equation by the substitution z = y1-n. This is describe as follows: Multiplying the above equation by y-n ,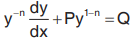
Let y1-n = z
Diff. w.r.t. x, (1- n). 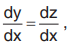
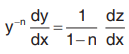
The equation becomes
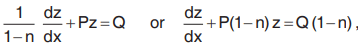
which is linear in z and x.
Differential Equations of first order and higher degree
A differential equation of first order and nth degree is of the form.
where p = dy/dx and P1, P2, … Pn are functions of x and y.
Equations solvable for p
The left hand side of (1) can be factorized into factors of the first degree then (1) becomes
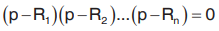
obtain a solution fix, y ,c = 0 corresponding to the equation p - Ri = 0 for i = 1, 2, … n.
Thus the general solution of (1) is given by
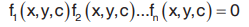
Equations solvable for y
The equation can be put in the form y = f(x, p) …(2)
Differentiating w.r.t. x we get 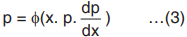
which is a first order and first degree differential equation with variables p and x.
On solving equation (3) we get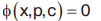
Eliminating p from (1) and (3) we get the required solution.
Equations solvable for x
The equation can be put in the form x = f(y, p)
Differentiating w.r.t. y we get

This is first order and first degree differential equation with variables p and y.
On solving equation (4) we get

Then eliminating p from (1) and (5) we get the required solution.
Note: The factor which does not involve a derivative of p with respect to x or y will always lead to singular solution. Hence such a factor can be omitted.
Clairaut’s Equation
The equation of the formy = px + f(p) …(1)
is called Clairaut’s equation.
Differentiating w.r.t. x we get
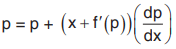
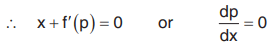
Now dp/dx = 0
∴ p = c (a constant)
Hence the general solution of (1) is
G.S. = y = cx + f(c) …(2)
if x + fc(p) = 0 we use equation (2) and (1) to obtain a solution. This solution is not included in the general solution (2). Such a solution is called a singular solution.
Note : Clairaut’s equation always has a singular solution
Solved Example 1 :Solve p2 - 5p + 6
Solution : Solving for p
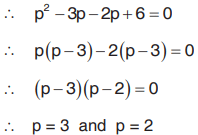
Where,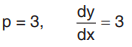
∴ y = 3x + C [Integrating]
When,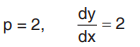
∴ y = 2x + C [Integrating]
∴ The solution is (y - 3x - C) (y - 2x - C)
Solved Example 2 : Solve xp2 - 2py + x = 0
Solution : Solving for p
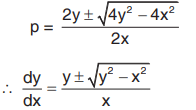
This is a homogenous equation in x and y
Put y = vx
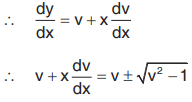
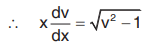
Separating the variables we get
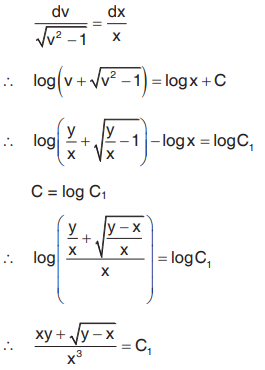
|
44 videos|109 docs|58 tests
|
FAQs on First-order equations (linear and nonlinear) - Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE)
| 1. What are First Order Linear Differential Equations? |  |
| 2. How do you reduce First Order Differential Equations to Linear form? |  |
| 3. What is Bernoulli’s Equation in the context of Differential Equations? |  |
| 4. What are Clairaut’s Equations and how are they different from First Order Linear Differential Equations? |  |
| 5. How are First Order Differential Equations of higher degree solved compared to First Order Linear Differential Equations? |  |
















