Functions of Single Variable | Engineering Mathematics for Electrical Engineering - Electrical Engineering (EE) PDF Download

A real valued function y = f(x) of a real variable x is a mapping whose domain S and co-domain R are sets of real numbers. The range of the function is the set 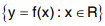 , which is a subset of R.

Limit of a function 

The function f is said to tend to the limit l as x → a, if for a given positive real number ε > 0 we can find a real number δ > 0 such that 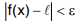 whenever  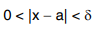Symbolically we write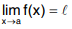

Left Hand and Right Hand Limits 
Let x < a and x → a from the left hand side.
If |f(x) - l₁ | < ε, a - δ < x < a or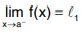
then l₁ is called the left hand limit.
Let x > a and x → a from the right hand side.
If |f(x) l₂ | < ε, a < x < a + δ or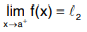
then l₂ is called the right hand limit.

If l_{1 = l2} then 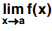 exists. If the limit exists then it is unique.

Clear all your Electrical Engineering (EE) doubts with EduRev Join for Free

Join for Free

Properties of Limits

Let f and g be two functions defined over S and let a be any point, not necessarily in S
Ans if 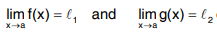 exist, then 

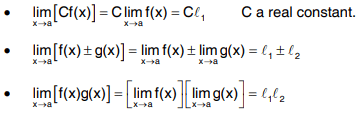
Standard Formulae

Download the notes Functions of Single Variable

Download as PDF

Download as PDF

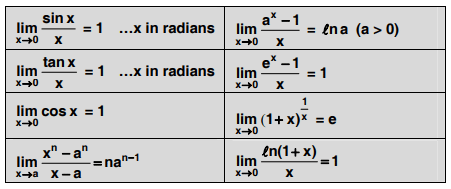
Solved Numericals

Q1. Show that 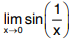 does not exist.
Solution : For different values of x in the interval 0 < | x | < δ the function 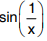 takes values between -1 and 1. Since  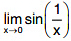is not unique limit does not exist 

Q2. Show that 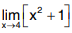does not exist, where [] is the greatest integer function
Solution : Let h > 0, we have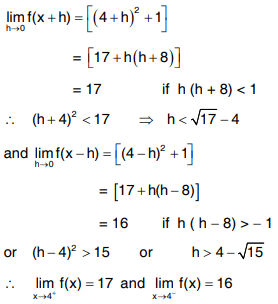

The limit does not exist.