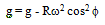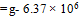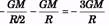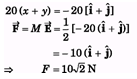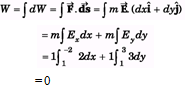NEET Exam > NEET Notes > Physics Class 11 > DC Pandey Solutions: Gravitation - 1
DC Pandey Solutions: Gravitation - 1 | Physics Class 11 - NEET PDF Download
Introductory Exercise 10.1
Q.1. Calculate the change in the value of g at altitude 45°. Take radius of earth = 6.37 × 103 km
Sol.
= g -0.0168 m/s2
Dg = g-g' = 0.0168 m/s2
Q.2. Determine the speed with which the earth would have to rotate on its axis, so that a person on the equator would weigh 3/5th as much as at present. Take R = 6400 km
Sol.
Q.3. At what height from the surface of earth will the value of g be reduced by 36% from the value at the surface? R = 6400 km
Sol.
Q.4. The distance between two bodies A and B is r. Taking the gravitational force according to the law of inverse square of r, the acceleration of the body A is a. If the gravitational force follows an inverse fourth power law, then what will be the acceleration of body A?
Sol.
Q.5. Find the force of attraction on a particle of mass m placed at the centre of a semicircular wire of length L and mass M.
Sol.
Introductory Exercise 10.2
Q.1. A particle of mass m is placed at the centre of a uniform spherical shell of same mass and radius R. Find the gravitational potential at a distance R/2 from the centre.
Sol.
V = Ve + Vs =
Q.2. A particle of mass 20 g experiences a gravitational force of 4.0 N along positive x-direction. Find the gravitational field at that point.
Sol.
200 N/kg i
Q.3. The gravitational potential due to a mass distribution is V = 3x2y + y3z. Find the gravitational field.
Sol.
Q.4. Gravitational potential at x = 2 m is decreasing at a rate of 10 J/kg-m along the positive x-direction. It implies that the magnitude of gravitational field at x = 2 m is also 10 N/kg. Is this statement true or false?
Sol. Only the variation is given along x-axis, nothing is about y and z axis, so, the statement is false.
Q.5. The gravitational potential in a region is given by, V = 20(x+ y) J/kg. Find the magnitude of the gravitational force on a particle of mass 0.5 kg placed at the origin.
Sol.
Q.6. The gravitational field in a region is given by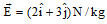
Find the work done by the gravitational field when a particle of mass 1 kg is moved on the line 3y + 2x = 5 from (1 m, 1 m) to (-2 m, 3 m).
Sol.
The document DC Pandey Solutions: Gravitation - 1 | Physics Class 11 - NEET is a part of the NEET Course Physics Class 11.
All you need of NEET at this link: NEET
|
92 videos|346 docs|98 tests
|
FAQs on DC Pandey Solutions: Gravitation - 1 - Physics Class 11 - NEET
| 1. What is the formula for gravitational force? |  |
Ans. The formula for gravitational force between two objects is given by Newton's law of universal gravitation, which states that the force is directly proportional to the product of the masses of the objects and inversely proportional to the square of the distance between them. Mathematically, it can be represented as:
F = G * (m1 * m2) / r^2
Where F is the gravitational force, G is the gravitational constant, m1 and m2 are the masses of the objects, and r is the distance between their centers.
| 2. How does the distance between two objects affect the gravitational force between them? | |
Ans. The gravitational force between two objects is inversely proportional to the square of the distance between them. This means that as the distance between the objects increases, the gravitational force decreases. Conversely, as the distance decreases, the gravitational force increases. Therefore, the closer the objects are to each other, the stronger the gravitational force between them.
| 3. What is the significance of the gravitational constant in the formula for gravitational force? | |
Ans. The gravitational constant (G) is a fundamental constant in physics that determines the strength of the gravitational force between two objects. It is a universal constant and has the same value everywhere in the universe. The value of G is approximately 6.674 × 10^-11 N(m/kg)^2. The significance of the gravitational constant is that it allows us to calculate the gravitational force accurately based on the masses and distances involved.
| 4. What is the difference between mass and weight in the context of gravity? | |
Ans. Mass and weight are often used interchangeably, but they have different meanings in the context of gravity. Mass is a measure of the amount of matter in an object and remains constant regardless of the gravitational field. On the other hand, weight is the force exerted on an object due to gravity and depends on the mass of the object and the strength of the gravitational field. Weight can vary depending on the location, as the strength of the gravitational field differs from one place to another.
| 5. How does the gravitational force affect the motion of celestial bodies in the universe? | |
Ans. The gravitational force plays a crucial role in determining the motion of celestial bodies in the universe. It is responsible for keeping planets in orbit around the sun, moons around planets, and stars in galaxies. The gravitational force between celestial bodies causes them to attract each other, resulting in the formation and maintenance of stable orbital paths. It is this force that keeps the celestial bodies in motion and prevents them from flying off into space.
About this Document
3.2K Views
4.61/5
Rating
Apr 24, 2025
Last updated
Document Description: DC Pandey Solutions: Gravitation - 1 for NEET 2025 is part of Physics Class 11 preparation.
The notes and questions for DC Pandey Solutions: Gravitation - 1 have been prepared according to the NEET exam syllabus. Information about DC Pandey Solutions: Gravitation - 1 covers topics
like Introductory Exercise 10.1, Introductory Exercise 10.2 and DC Pandey Solutions: Gravitation - 1 Example, for NEET 2025 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for DC Pandey Solutions: Gravitation - 1.
Introduction of DC Pandey Solutions: Gravitation - 1 in English is available as part of our Physics Class 11
for NEET & DC Pandey Solutions: Gravitation - 1 in Hindi for Physics Class 11 course.
Download more important topics related with notes, lectures and mock test series for NEET
Exam by signing up for free. NEET: DC Pandey Solutions: Gravitation - 1 | Physics Class 11 - NEET
Description
Full syllabus notes, lecture & questions for DC Pandey Solutions: Gravitation - 1 | Physics Class 11 - NEET - NEET | Plus excerises question with solution to help you revise complete syllabus for Physics Class 11 | Best notes, free PDF download
Information about DC Pandey Solutions: Gravitation - 1
In this doc you can find the meaning of DC Pandey Solutions: Gravitation - 1 defined & explained in the simplest way possible. Besides explaining types of
DC Pandey Solutions: Gravitation - 1 theory, EduRev gives you an ample number of questions to practice DC Pandey Solutions: Gravitation - 1 tests, examples and also practice NEET
tests
Related Searches
Sample Paper
,DC Pandey Solutions: Gravitation - 1 | Physics Class 11 - NEET
,video lectures
,mock tests for examination
,ppt
,practice quizzes
,DC Pandey Solutions: Gravitation - 1 | Physics Class 11 - NEET
,Objective type Questions
,Semester Notes
,MCQs
,past year papers
,Summary
,Exam
,Previous Year Questions with Solutions
,Extra Questions
,shortcuts and tricks
,Free
,study material
,DC Pandey Solutions: Gravitation - 1 | Physics Class 11 - NEET
,Important questions
,Viva Questions
;
Additional Information about DC Pandey Solutions: Gravitation - 1 for NEET Preparation
DC Pandey Solutions: Gravitation - 1 Free PDF Download
The DC Pandey Solutions: Gravitation - 1 is an invaluable resource that delves deep into the core of the NEET exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the DC Pandey Solutions: Gravitation - 1 now and kickstart your journey towards success in the NEET exam.
Importance of DC Pandey Solutions: Gravitation - 1
The importance of DC Pandey Solutions: Gravitation - 1 cannot be overstated, especially for NEET aspirants.
This document holds the key to success in the NEET exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
DC Pandey Solutions: Gravitation - 1 Notes
DC Pandey Solutions: Gravitation - 1 Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to DC Pandey Solutions: Gravitation - 1.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, DC Pandey Solutions: Gravitation - 1 Notes on EduRev are your ultimate resource for success.
DC Pandey Solutions: Gravitation - 1 NEET Questions
The "DC Pandey Solutions: Gravitation - 1 NEET Questions" guide is a valuable resource for all aspiring students preparing for the
NEET exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study DC Pandey Solutions: Gravitation - 1 on the App
Students of NEET can study DC Pandey Solutions: Gravitation - 1 alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the DC Pandey Solutions: Gravitation - 1,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of DC Pandey Solutions: Gravitation - 1 is prepared as per the latest NEET syllabus.
|
© EduRev
|
Education Revolution
|
|
Signup to see your scores
go up within 7 days!
Access 1000+ FREE Docs, Videos and Tests
Takes less than 10 seconds to signup