Class 10 Maths Chapter 5 HOTS Questions - Arithmetic Progressions
HOTS Questions
Q1: Find the ‘6th’ term of the A.P.: 2m + 1m, 2m - 1m, 2m - 3m, ...
Solution: Here,
a1 = 2m + 1m, a2 = 2m - 1m
∴ d = a2 - a1
= 2m - 1m − 2m + 1m
= 2m - 1 - 2m - 1m = -2m
Now, an = a + (n – 1)d
an = 2m + 1m + (n - 1) -2m
= 2m + 1m + -2n + 2m
= 2m + 1 - 2n + 2m = 2m - 2n + 3m
Thus, the nth term is = 2m - 2n + 3m
Again, we have:
an = 2m - 2n + 3m
⇒ a6 = 2m - 2(6) + 3m = 2m - 12 + 3m
= 2m - 9m
i.e., the 6th term is: (2m - 9m)
Q2: If the ratio of the sum of first n terms of two A.P.'s is (7n + 1) : (4n + 27), find the ratio of their mth terms.
Sol: Let the first terms of given AP's be a1 and a2, common differences be d1 and d2 and let Sn and the sum of n terms.
∴ The sum of the first n terms of an arithmetic progression (A.P.) is:
Sn = n2 × [2a1 + (n - 1)d1])
Similarly, for the second A.P., the sum is:
S'n = n2 × [2a2 + (n - 1)d2])
Given: SnS'n = 7n + 14n + 27
Substituting the values of \(Sn\) and \(S'n\), we get:
SnS'n = n2 × [2a1 + (n - 1)d1]n2 × [2a2 + (n - 1)d2] = 7n + 14n + 27
Simplifying the fractions:
SnS'n = 2a1 + (n - 1)d12a2 + (n - 1)d2 = 7n + 14n + 27
Now, replacing n by (2m-1) for getting ratio of mth terms of given APs,
2a1 + (2m - 2)d12a2 + (2m - 2)d2 = 7(2m - 1) + 14(2m - 1) + 27
Simplifying:
⇒ a1 + (m - 1)d1a2 + (m - 1)d2 = 14m - 7 + 18m - 4 + 27
= 14m - 68m + 23
Or:
a1 + (m - 1)d1a2 + (m - 1)d2 = 14m - 68m + 23
Thus, the required ratio of mth term of given AP's is (14m – 6) : (8m + 23)
Q3: If the numbers a, b, c, d and e form an A.P., then find the value of a – 4b + 6c – 4d + e
Sol: We have the first term of A.P. as ‘a’.
Let D be the common difference of the given A.P.,
Then :
b = a + D, c = a + 2D, d= a + 3D and e = a + 4D
∴ The 2nd term = a + {common difference}
The 3rd term = a + 2 , {common difference} etc.
∴ a – 4b + 6c – 4d + e
= a – 4(a + D ) + 6 (a + 2D) – 4 (a + 3D) + (a + 4D)
= a – 4a + 6a – 4a + a – 4D + 12D – 12D + 4D
= 8a – 8a + 16D – 16D = 0
Thus, a – 4b + 6c – 4d + e = 0
Q4: If an+1 + bn+1an + bn is the arithmetic mean between ‘a’ and ‘b’, then, find the value of ‘n’.
Sol: Note: A.M., between ‘a’ and ‘b ’= 1/2
(a + b)
We know that :
A.M. between ‘a’ and ‘b’ = a + b/2
It is given that,
If an+1 + bn+1an + bn is the A.M. between 'a' and 'b', then:
∴ an+1 + bn+1an + bn = a + b2
By cross multiplication, we get :
2 × [an+1 + bn+1] = [an + bn][a + b]
⇒2an + 1 + 2bn + 1 = an + 1 + abn + anb + bn + 1
⇒ 2an + 1 – an + 1 + 2bn + 1– bn + 1= abn + anb
⇒ an + 1 + bn + 1 = abn +anb
⇒ an+1 – anb = abn – bn+1
⇒ an[a–b] = bn[a –b]
⇒ anbn = (a - b)(a - b) = 1
⇒ (ab)n = (ab)0 = 1 [∴ x0 = 1]
⇒ n = 0
Q5: Solve the equation :
1 + 4 + 7 + 10 + ... + x = 287
Sol: 
Since,
∴ a = 1,d = 3 and an = x
∴ an = a + (n – 1)d
⇒ x = 1 + (n – 1) 3 or x = 3n – 2
Also, Sn = n/2 (a+l)
⇒ 287 = n2 (1 + x)
⇒ 2(287) = n[1 + (3n – 2)]
⇒ 574 = n[3n – 1]
⇒ 3n2 – n – 574 = 0
Solving the above quadratic equation, we get
n = -(-1) ± √(1 + 4 × 3 × 574)6 = 1 ± √68886
or n = 1 ± 836 ⇒ n = 14 or -413
But, negative n is not desirable.
∴ n = 14
x = 3n – 2
Now, x = 3(14) – 2 = 42 – 2 = 40
Thus, x = 40
Q6: Find three numbers in A.P. whose sum is 21 and their product is 231.
Sol: Let the three numbers in A.P. are:
a – d, a, a + d
∴ (a – d) + a + (a + d) = 21
⇒ a – d + a + a + d = 21
or 3a = 21 ⇒ a = 7
Also, (a – d) × a × (a + d) = 231
∴ (7 – d) × 7 × (7 + d) = 231
⇒ (7 – d) (7 + d) × 7 = 231
⇒ 72 – d2 = 231 /7 = 33
⇒ 49 – d2 = 33
or d2 = 49 – 33 = 16
⇒ d = ± 4
Now, when d = 4, then three numbers in AP are : (7 – 4), 7, (7 + 4) i.e. 3, 7, 11.
When d = –4, then three numbers in AP are : [7 – (–4)], 7, [7 + (–4)]
or 11, 7, 3
Q7: The ninth term of an A.P. is equal to seven times the second term and twelfth term exceeds five times the third term by 2. Find the first term and common difference.
Sol: Let 'a' be the first term and 'd' be the common difference
Since, an = a + (n–1)d
∴ a9 = a + 8d and a12 = a + 11d
Also a2 = a + d and a3 = a + 2d
since a9 = 7a2 and a12 = 5a3 + 2
or a9 = 7 (a + d) ⇒ a9 = 7a + 7d ... (1)
a12 = 5 (a + 2d) + 2
⇒ a12 = 5a + 10d + 2 ... (2)
Now, a + 8d = 7a + 7d [From (1)]
or – 6a + d = 0 ... (3)
Also a + 11d = 5a + 10d + 2 [From (2)]
or –4a + d = 2 ... (4)
Subtracting (4) from (3), we have
–2a = –2 ⇒ a = 1
Now, from (3), –6 + d = 0 ⇒ d = 6
Thus, a = 1 and d = 6
Value-Based Questions
Q1: Savita has two options to buy a house:
(a) She can pay a lumpsum amount of ₹ 22,00,000
Or
(b) She can pay ₹ 4,00,000 cash and balance in 18 annual instalments of ₹ 1,00,000 plus 10% interest on the unpaid amount.
She prefers option
(i) and donates 50% of the difference of the costs in the above two options to the Prime Minister Relief Fund.
(i) What amount was donated to Prime Minister Relief Fund?
(ii) Which mathematical concept is used in the above problem?
(iii) By choosing to pay a lumpsum amount and donating 50% of the difference to the Prime Minister Relief Fund, which value is depicted by Savita?
Sol:
(a) Total cost of the house = ₹ 22,00,000
(b) Cash payment = ₹ 4,00,000
Balance = ₹ 22,00,000 – ₹ 4,00,000 = ₹ 18,00,000
1st instalment = ₹ [1,00,000 + 10% of balance]
= ₹ [1,00,000 + 10100 × 18,00,000]
= ₹ [1,00,000 + 1,80,000] = ₹ 2,80,000
Balance after 1st instalment = ₹ [18,00,000 – 1,00,000] = ₹ 17,00,000
2nd instalment = ₹ [1,00,000 + 10% of 17,00,000]
= ₹ [1,00,000 + 1,70,000] = ₹ [2,70,000]
Balance after 2nd instalment = ₹ 17,00,000 – ₹ 1,00,000 = ₹ 16,00,000
∵ 3rd instalment = ₹ [1,00,000 + 10% of 16,00,000]
= ₹ [1,00,000 + 1,60,000] = ₹ 2,60,000
... and so on.
∵ Total amount in instalments = ₹ 2,80,000 + ₹ 2,70,000 + ₹ 2,60,000 + ..... to 18 terms
= n2 [2a + (n − 1)d], where a = 2,80,000, d = −10,000, n = 18
= 182 [2(2,80,000) + (18 − 1)(−10,000)]
= ₹ 9 [560,000+17(-10,000)
= ₹ 9 [560,000 - 170,000]
= ₹ 9 = [390,000] = ₹ 35,10,000
∴ Total cost of house = ₹ 35,10,000 + 4,00,000 = ₹ 39,10,000
Difference in costs of the house in two options
= ₹ 39,10,000 – ₹ 22,00,000 = ₹ 17,10,000
∴ (i) Amount donated towards Prime Minister Relief Fund = 50% of ₹ 17,10,000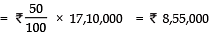
(ii) Arithmetic Progressions
(iii) National Loyalty
Q2: In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be double of the class in which they are studying. If there are 1 to 12 classes in the school and each class has two sections, find how many trees were planted by the students. Which value is shown in this question?
Sol: ∴ There are 12 classes in all.
Each class has 2 sections.
∴ Number of plants planted by class I = 1 x 2 = 2
Number of plants planted by class II = 2 x 2 = 4
Number of plants planted by class III = 3 x 2 = 6
Number of plants planted by class IV = 4 x 2 = 8
......................................................................................................
......................................................................................................
Number of plants planted by class XII = 12 x 2 = 24
The numbers 2, 4, 6, 8, ........................ 24 forms an A.P.
Here, a = 2, d = 4 – 2 = 2
∵ Number of classes = 12
∴ Number of terms (n) = 12
Now, the sum of n terms of the above A.P., is given by Sn = n/2 [2a+(n-1)d]
∴ S12 = 12/2 [2(2) -(12)-1) 2]
= 6 [4 + (11 x 2)]
= 6 x 26 = 156
Thus, the total number of trees planted = 156
Value shown: To enrich polution free environment.
|
126 videos|457 docs|75 tests
|
FAQs on Class 10 Maths Chapter 5 HOTS Questions - Arithmetic Progressions
| 1. What is an arithmetic progression (AP) and how is it defined? |  |
| 2. How can I find the nth term of an arithmetic progression? |  |
| 3. What is the formula to calculate the sum of the first n terms of an arithmetic progression? |  |
| 4. Can you explain how to determine if a sequence is an arithmetic progression? |  |
| 5. How can I solve real-life problems using arithmetic progressions? |  |























