Heat, Internal Energy and Work | Physics Class 11 - NEET PDF Download

Introduction to Heat, Internal Energy, and Work

• Understanding the functioning of a heat engine and the microscopic movements within a glass of water unveils the realm of internal energy. Thermodynamics, the study of heat and work effects on state changes, is governed by fundamental rules known as thermodynamic laws.
• Energy generated or absorbed during chemical processes transforms following thermodynamic principles. Energy cannot be created or destroyed, only converted from one form to another, forming the basis of energy transformation utilized across various sectors.
  Thermodynamics delves into the transfer of energy between different forms, exploring the intricate relationship between heat, temperature, energy, and work involved.

Thermodynamic System

Thermodynamics and Internal Energy

When we explore the realm of thermodynamics, we delve into the world of energy transformations. Steam engines, like those powering trains, exemplify this concept vividly. They harness steam energy to propel pistons back and forth, subsequently converting this motion into rotational force that drives the wheels.

Understanding Internal Energy

Internal energy encapsulates the combined kinetic energy from particle motion and potential energy from molecular arrangement within a system. It remains influenced by temperature and initial and final states, irrespective of the path taken. Notably, the internal energy of an ideal gas hinges solely on temperature, while a real gas' internal energy considers both temperature and volume.

• The unit of measurement for internal energy is the Joule (J).
• Symbolically, internal energy is denoted by the letter U.

Internal Energy Formula

The formula illustrating internal energy is succinctly stated as:

ΔU = Q - W

Here, ΔU signifies the system's internal energy, with Q representing heat input and W denoting work output.

Understanding Internal Energy, Enthalpy, and Heat in Thermodynamics

• ΔU represents the internal energy of a system.
• Q stands for the heat supplied to the system.
• W signifies the work done by the system.

Relation between Enthalpy and Internal Energy

In the context of ideal gases, the connection between internal energy and enthalpy is elucidated. It is mathematically demonstrated that the internal energy of an ideal gas is solely reliant on temperature.

The internal energy (U) for an ideal gas is expressed as U = U(T).

In contrast, enthalpy (H) is defined as H = U + PV ... (1), where P represents pressure, and V signifies the volume of the ideal gas.

• P denotes pressure.
• V denotes volume.

By incorporating the ideal gas equation PV = RT into the above equation, we derive H = U + RT.

Additionally, the enthalpy of an ideal gas is articulated as H = H(T).

Furthermore, the specific heats at constant volume and pressure (Cv and Cp), which are temperature-dependent, are described by dU = Cv(T) dT and dH = Cp(T) dT, respectively.

The specific heat ratio k, signifying Cp/Cv, further illustrates the relationship between internal energy and enthalpy for an ideal gas.

Heat in Thermodynamics

Heat, defined as energy in transit within thermodynamics, represents the kinetic energy of molecules in motion. It plays a pivotal role in optimizing operations for process designers and engineers, aiding in the efficient capture of energy associated with chemical processes.

Heat naturally flows from regions of higher to lower temperatures, a fundamental principle underpinning the development of various heat engines. When temperature differentials exist, heat serves as the energy in transit.

Internal energy, encompassing internal kinetic and potential energy arising from molecular interactions, distinguishes heated bodies from cold ones of equivalent size.

Heat and Work in Thermodynamics

• The concept of heat transfer in a system involves categorizing heat entering as positive and heat leaving as negative.
• Factors influencing heat flow include:
  • The mass of the substance (m).
  • The temperature difference between the two objects (ΔT).
  • The nature of the substance.
• This relationship can be expressed as:
  • Q ∝ mΔT
  • or
  • Q = cmΔT
• where 'c' represents the specific heat capacity, a constant unique to the substance.

Work in Thermodynamics

• Work in thermodynamics refers to the energy exchanged between a system and its surroundings.
• Variables affecting work include external forces, temperature, pressure, and volume changes.
• Work can be done by a gas during expansion (positive) and on a gas during compression (negative).
  • Expansion: Gas does work and the value is positive.
  • Compression: Gas has work done on it, resulting in a negative value.

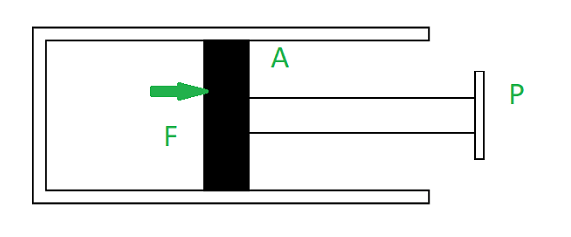Work done by the gas on a piston

The formula for work done is represented as:

W = ∫P.dV

Sample Problems

• Problem 1. When a piece of ice is placed on your hand, why do you feel a cold sensation?

  Explanation:

  Feeling a cold sensation when ice is placed on your hand occurs because the temperature of the ice is lower than that of your hand. Heat transfers from the warmer body (hand) to the colder body (ice).

• Problem 2. Is it possible to determine the absolute value of internal energy? Why or why not?

  Explanation:

  The absolute value of internal energy cannot be precisely determined since it comprises various forms of energy, some of which are not directly measurable.

• Problem 3. What factors influence the internal energy of a system?

  Explanation:

  Temperature and volume play crucial roles in altering the internal energy of a system. As the system's temperature rises, molecules gain speed, leading to increased kinetic energy.

• Problem 4. Calculation involving a cylinder with a movable piston and gas

  Problem setup:

  A cylinder with a movable piston contains gas and a heavy block. The total mass of the block and piston is 51 kg. If 1070 J of heat enters the gas, causing its internal energy to rise by 790 J, what will be the piston's displacement?

  Given:

  • Total heat supplied = work done + change in internal energy

Work and Energy

• Problem 1. Calculating Work Done

  Given: Work done = 280 J, Force (F) = 51 N

  Calculate the distance moved by the piston (s).

  Formula: Work (W) = Force (F) x Distance (s)

  Distance Moved: s = 280 / F

  s = 280 / (51 x 10)

  s = 0.54 meters

• Problem 2. Internal Energy Change

  An electric heater supplies heat at 50 W and work done is 25 J/s.

  Find the rate of increase in internal energy.

  Given: Heat supplied (Q) = 50 W, Work done (W) = 25 J/s

  Internal Energy Change: Q = ΔU + W

  ΔU = Q - W = 50 - 25 = 25 J/s

  The internal energy increases at a rate of 25 J/s.