UPSC Exam > UPSC Notes > Chemistry Optional Notes for UPSC > Huckel's Rule: What Does 4n+2 Mean?
Huckel's Rule: What Does 4n+2 Mean? | Chemistry Optional Notes for UPSC PDF Download
Stop Looking For “n” In A Molecule, Because You’re Looking For The Wrong Thing
The other night a student came to me with a question about aromaticity.
“There’s one thing I don’t get”, she said. “They say a molecule has to have 4n+2 electrons to be aromatic. How do you find ‘n’ ?”
Teachable moment!
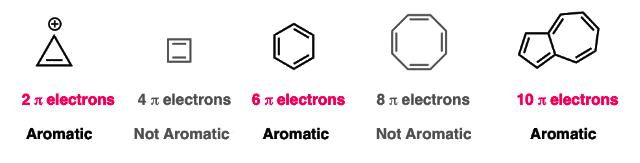
These are aromatic molecules containing (4n+2) pi electrons, where “n” is a natural number
Count the pi-electrons - don’t look for “n” !
In the [4n+2] Rule (“Huckel’s Rule”), “n” Is Not A Characteristic of The Molecule!
“n” is not a characteristic of the molecule! Let me explain.
In order for a molecule to be aromatic, it has to have the following characteristics:
- It must be cyclic
- It must be conjugated (i.e. all atoms around the ring must be able to participate in π-bonding through resonance)
- It must be flat
And, it must have a certain number of π-electrons. This is known as Huckel’s rule. The number of π electrons must equal one of the numbers in this series:
2, 6, 10, 14, 18….and so on. For example, we can find aromatic molecules with 2 pi electrons, 6 pi electrons, 10 pi electrons, 14 pi electrons, 18 pi electrons, and so on.
But we have never found aromatic molecules with 0, 1, 3, 4, 5, 7, 9, 11, 12, 13, 15, 16, 17 (and so on) pi electrons. Those numbers are not in the series.
To reprise: the number of pi electrons in an aromatic molecule will always be found in the series [2, 6, 10, 14, 18 …and so on]
However, there has to be a better way of expressing it than [2, 6, 10, 14, 18… and so on”]. Right?
Question for Huckel's Rule: What Does 4n+2 Mean?Try yourself: How can a molecule be considered aromatic?View Solution
In Huckel’s Rule, The Formula (4n+2) Is An Algebraic Expression Of The Series 2, 6, 10, 14… Where ‘n’ Is A Natural Number
There is! This is where we use algebra. This is where n is going to come in – we are going to use math (algebra) to replace “2, 6, 10, 14, 18… and so on” with a condensed formula.
2, 6, 10, 14, 18… is an example of an algebraic series.
Algebraically, you can express this with the formula (4n +2), where n is a natural number (0, 1, 2, 3…)
Let’s plug in different values of n (we will put n in bold)
For the formula 4n + 2
- For n = 0, we get (4 × 0 + 2) = 2
- For n = 1, we get (4 × 1 + 2) = 6
- For n = 2, we get (4 × 2 + 2) = 10
- For n = 3, we get (4 × 3 + 2) = 14
- For n = 4, we get (4 × 4 + 2) = 18
We can keep going, but do you get the idea?
By using the formula [4n +2], we are expressing the same idea as [2, 6, 10, 14, 18… and so on] but it is a lot more condensed – and precise.
Summary: “n” Comes From Algebra, NOT From Chemistry
Molecules that have the 3 characteristics listed above (cyclic, conjugated, flat) and have this number of π electrons [4n +2] will be aromatic.
The letter “n” is not a characteristic of the molecule!
Question for Huckel's Rule: What Does 4n+2 Mean?Try yourself: What is the algebraic expression for the series 2, 6, 10, 14...?View Solution
The document Huckel's Rule: What Does 4n+2 Mean? | Chemistry Optional Notes for UPSC is a part of the UPSC Course Chemistry Optional Notes for UPSC.
All you need of UPSC at this link: UPSC
FAQs on Huckel's Rule: What Does 4n+2 Mean? - Chemistry Optional Notes for UPSC
| 1. What is the [4n 2] rule in Huckel's rule? |  |
Ans. The [4n 2] rule in Huckel's rule is an algebraic expression that determines whether a molecule is aromatic or not. It states that if a molecule has a conjugated pi system with a total number of pi electrons given by the formula (4n + 2), where 'n' is a natural number, then the molecule is aromatic.
| 2. What does 'n' represent in the [4n 2] rule? | |
Ans. In the [4n 2] rule, 'n' is a variable that represents a natural number. It is used in the algebraic expression (4n + 2) to calculate the total number of pi electrons in a conjugated pi system. The value of 'n' can be any positive integer such as 1, 2, 3, and so on.
| 3. Is 'n' a characteristic of the molecule in Huckel's rule? | |
Ans. No, 'n' is not a characteristic of the molecule in Huckel's rule. It is a variable used in the algebraic expression (4n + 2) to determine the total number of pi electrons in a conjugated pi system. The value of 'n' depends on the number of pi electrons and does not describe any specific property or characteristic of the molecule itself.
| 4. How can the [4n 2] rule be applied to determine aromaticity? | |
Ans. To apply the [4n 2] rule to determine aromaticity, one needs to count the number of pi electrons in the conjugated pi system of the molecule. If the total number of pi electrons can be expressed as (4n + 2), where 'n' is a natural number, then the molecule is aromatic. If the total number of pi electrons does not fit this expression, the molecule is not aromatic.
| 5. What is the significance of the [4n 2] rule in organic chemistry? | |
Ans. The [4n 2] rule is significant in organic chemistry as it provides a simple and useful guideline to determine the aromaticity of conjugated pi systems. Aromatic molecules have unique stability and reactivity compared to non-aromatic molecules. By applying the [4n 2] rule, chemists can quickly assess the aromaticity of various organic compounds, which helps in predicting their properties and behavior.
Related Exams
About this Document
|
Nov 21, 2024 Last updated |
Document Description: Huckel's Rule: What Does 4n+2 Mean? for UPSC 2024 is part of Chemistry Optional Notes for UPSC preparation.
The notes and questions for Huckel's Rule: What Does 4n+2 Mean? have been prepared according to the UPSC exam syllabus. Information about Huckel's Rule: What Does 4n+2 Mean? covers topics
like In the [4n+2] Rule (“Huckel’s Rule”), “n” Is Not A Characteristic of The Molecule!, In Huckel’s Rule, The Formula (4n+2) Is An Algebraic Expression Of The Series 2, 6, 10, 14… Where ‘n’ Is A Natural Number, Summary: “n” Comes From Algebra, NOT From Chemistry and Huckel's Rule: What Does 4n+2 Mean? Example, for UPSC 2024 Exam. Find important definitions, questions, notes, meanings, examples, exercises and tests below for Huckel's Rule: What Does 4n+2 Mean?.
Introduction of Huckel's Rule: What Does 4n+2 Mean? in English is available as part of our Chemistry Optional Notes for UPSC
for UPSC & Huckel's Rule: What Does 4n+2 Mean? in Hindi for Chemistry Optional Notes for UPSC course.
Download more important topics related with notes, lectures and mock test series for UPSC
Exam by signing up for free. UPSC: Huckel's Rule: What Does 4n+2 Mean? | Chemistry Optional Notes for UPSC
Description
Full syllabus notes, lecture & questions for Huckel's Rule: What Does 4n+2 Mean? | Chemistry Optional Notes for UPSC - UPSC | Plus excerises question with solution to help you revise complete syllabus for Chemistry Optional Notes for UPSC | Best notes, free PDF download
Information about Huckel's Rule: What Does 4n+2 Mean?
In this doc you can find the meaning of Huckel's Rule: What Does 4n+2 Mean? defined & explained in the simplest way possible. Besides explaining types of
Huckel's Rule: What Does 4n+2 Mean? theory, EduRev gives you an ample number of questions to practice Huckel's Rule: What Does 4n+2 Mean? tests, examples and also practice UPSC
tests
|
Explore Courses for UPSC exam
|
|
Signup for Free!
Signup to see your scores go up within 7 days! Learn & Practice with 1000+ FREE Notes, Videos & Tests.
Related Searches
Huckel's Rule: What Does 4n+2 Mean? | Chemistry Optional Notes for UPSC
,shortcuts and tricks
,Semester Notes
,study material
,Huckel's Rule: What Does 4n+2 Mean? | Chemistry Optional Notes for UPSC
,practice quizzes
,Huckel's Rule: What Does 4n+2 Mean? | Chemistry Optional Notes for UPSC
,Previous Year Questions with Solutions
,MCQs
,mock tests for examination
,Exam
,Sample Paper
,Objective type Questions
,Viva Questions
,Extra Questions
,past year papers
,Important questions
,Summary
,ppt
,video lectures
,Free
;
Additional Information about Huckel's Rule: What Does 4n+2 Mean? for UPSC Preparation
Huckel's Rule: What Does 4n+2 Mean? Free PDF Download
The Huckel's Rule: What Does 4n+2 Mean? is an invaluable resource that delves deep into the core of the UPSC exam.
These study notes are curated by experts and cover all the essential topics and concepts, making your preparation more efficient and effective.
With the help of these notes, you can grasp complex subjects quickly, revise important points easily,
and reinforce your understanding of key concepts. The study notes are presented in a concise and easy-to-understand manner,
allowing you to optimize your learning process. Whether you're looking for best-recommended books, sample papers, study material,
or toppers' notes, this PDF has got you covered. Download the Huckel's Rule: What Does 4n+2 Mean? now and kickstart your journey towards success in the UPSC exam.
Importance of Huckel's Rule: What Does 4n+2 Mean?
The importance of Huckel's Rule: What Does 4n+2 Mean? cannot be overstated, especially for UPSC aspirants.
This document holds the key to success in the UPSC exam.
It offers a detailed understanding of the concept, providing invaluable insights into the topic.
By knowing the concepts well in advance, students can plan their preparation effectively.
Utilize this indispensable guide for a well-rounded preparation and achieve your desired results.
Huckel's Rule: What Does 4n+2 Mean? Notes
Huckel's Rule: What Does 4n+2 Mean? Notes offer in-depth insights into the specific topic to help you master it with ease.
This comprehensive document covers all aspects related to Huckel's Rule: What Does 4n+2 Mean?.
It includes detailed information about the exam syllabus, recommended books, and study materials for a well-rounded preparation.
Practice papers and question papers enable you to assess your progress effectively.
Additionally, the paper analysis provides valuable tips for tackling the exam strategically.
Access to Toppers' notes gives you an edge in understanding complex concepts.
Whether you're a beginner or aiming for advanced proficiency, Huckel's Rule: What Does 4n+2 Mean? Notes on EduRev are your ultimate resource for success.
Huckel's Rule: What Does 4n+2 Mean? UPSC Questions
The "Huckel's Rule: What Does 4n+2 Mean? UPSC Questions" guide is a valuable resource for all aspiring students preparing for the
UPSC exam. It focuses on providing a wide range of practice questions to help students gauge
their understanding of the exam topics. These questions cover the entire syllabus, ensuring comprehensive preparation.
The guide includes previous years' question papers for students to familiarize themselves with the exam's format and difficulty level.
Additionally, it offers subject-specific question banks, allowing students to focus on weak areas and improve their performance.
Study Huckel's Rule: What Does 4n+2 Mean? on the App
Students of UPSC can study Huckel's Rule: What Does 4n+2 Mean? alongwith tests & analysis from the EduRev app,
which will help them while preparing for their exam. Apart from the Huckel's Rule: What Does 4n+2 Mean?,
students can also utilize the EduRev App for other study materials such as previous year question papers, syllabus, important questions, etc.
The EduRev App will make your learning easier as you can access it from anywhere you want.
The content of Huckel's Rule: What Does 4n+2 Mean? is prepared as per the latest UPSC syllabus.
|
© EduRev
|
Education Revolution
|
Follow Us
|
Signup on EduRev and stay on top of your study goals
10M+ students crushing their study goals daily