Introduction to Wave Optics | Physics Class 12 - NEET PDF Download
| Table of contents |

|
| Wave Optics |

|
| Wavefront |

|
| Huygen’s Principle |

|
| Maxwell’s Electromagnetic Wave Theory |

|
| Interference of Light |

|
| Llyod’s Mirror |

|
| Doppler's Effect in Light |

|
Wave Optics
Wave optics describes the connection between waves and rays of light.
- The wave theory states that light is a form of energy traveling as a transverse wave in a medium.
- The speed of light in a vacuum is a constant, and it is the speed in a medium that changes.
- This theory helps us understand complex phenomena like interference, diffraction, and polarization, where light behaves more like a wave than a particle.
- Wave optics gives us deeper insight into how light interacts with materials and affects various technologies like lenses, microscopes, and optical fibers.
Here are different theories listed based on wave theory: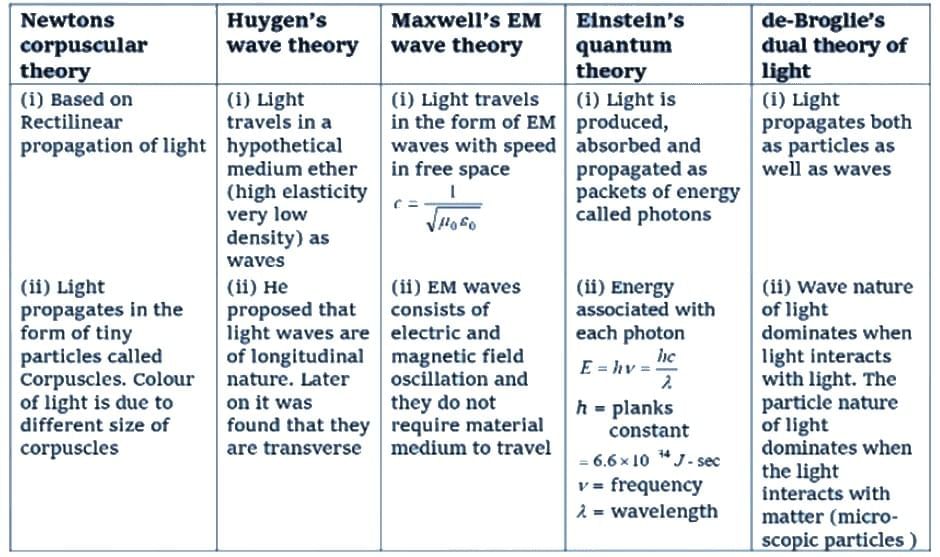
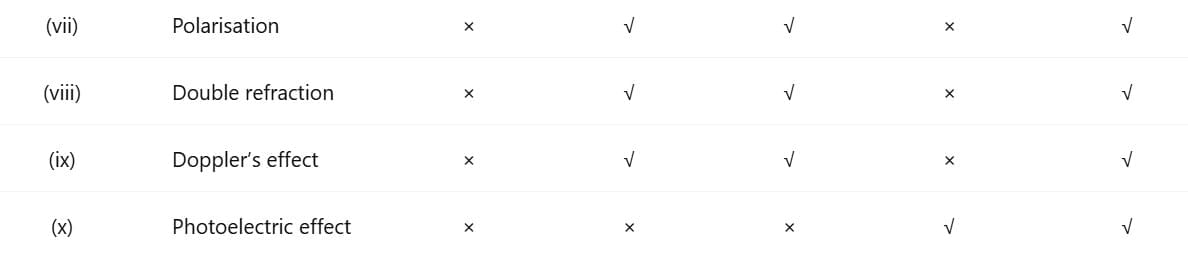
Here are some optical phenomena that are either explained (✔) or not explained (✖) by the different theories of light :

Wavefront
A wavefront is defined as the continuous locus of all the particles of a medium, which are vibrating in the same phase.
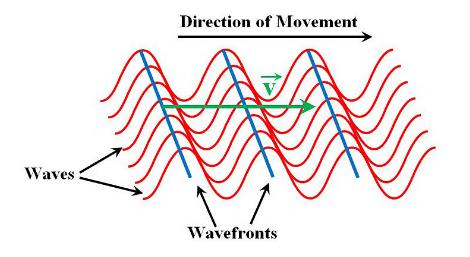 Wavefront
Wavefront
- It was suggested by Huygens.
- The direction of propagation of light (ray of light) is perpendicular to the wave front.
- There are three types of wavefront:
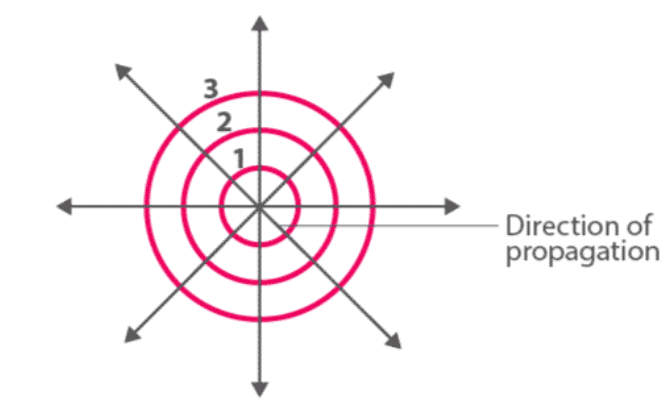
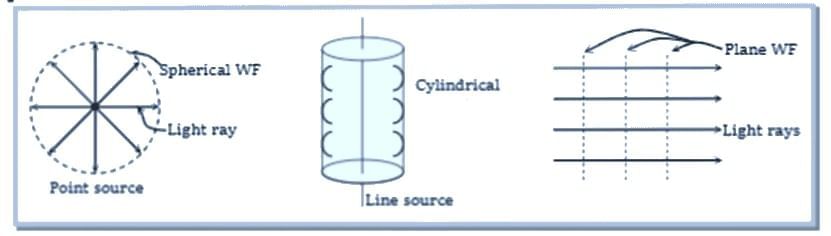
(a) Spherical wavefront - When light originates from a point source, the wavefronts take on a spherical shape.

∴ Intensity (I) ∝ (Amplitude)2
(b) Cylindrical wavefront - When the light comes from a linear source, the wavefronts are cylindrical in shape, with all points being equally distant from the source.
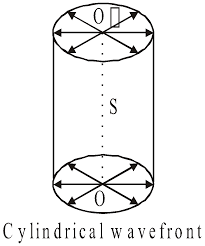

(c) Plane wavefront - When light comes from a distant source, the wavefronts become flat, or planar. In a plane wavefront, the amplitude stays the same, which means the intensity also remains constant.
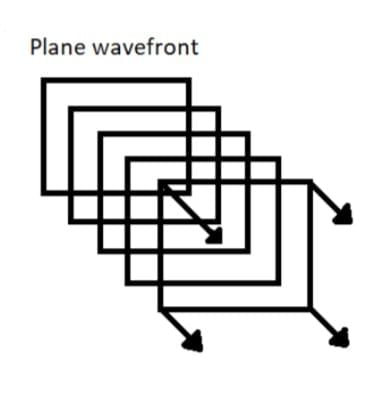
- Each point on a wavefront acts as a source of a new disturbance, known as secondary wavelets. These wavelets spread out in all directions at the speed of light in the medium.
- A surface that touches these secondary wavelets tangentially and moves forward at any moment creates the new wavefront at that instant. This is known as the secondary wavefront.
TIP: Imagine wavefronts like the ripples that form on a pond when you toss a stone into the water. The expanding circles are similar to spherical wavefronts in light.
 Ripples on a Pond
Ripples on a Pond
Huygen’s Principle
A wavefront at any instant is the collection of all particles in a medium that are disturbed simultaneously and are in the same phase of vibration.- According to Huygen's Principle, each point on a wavefront acts as a source of secondary disturbances, emitting spherical waves called secondary wavelets. These wavelets spread out in all directions at the speed of light as long as they stay in the same medium.
- The new wavefront is formed by the envelope or boundary of these secondary wavelets moving forward, giving the wavefront's position at a later time.
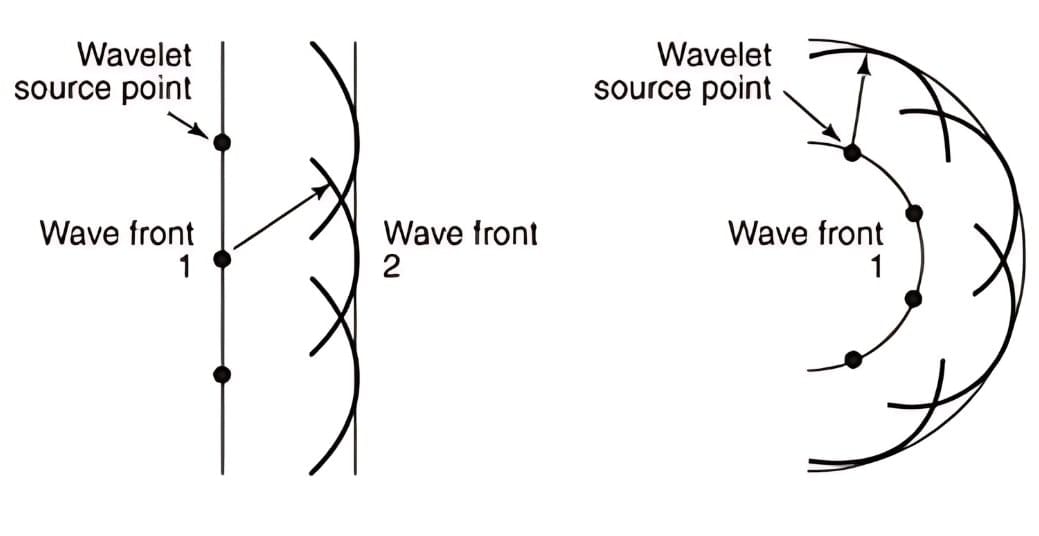 Huygen's Principle
Huygen's Principle
Maxwell’s Electromagnetic Wave Theory
According to Maxwell’s Electromagnetic (EM) Wave Theory, light waves arise from changing electric and magnetic fields. These changing fields cause the propagation of electromagnetic waves, or light waves.
Key points of this theory are:
- Energy is continuously emitted from a source as radiation, called radiant energy.
- The radiation consists of electric and magnetic fields oscillating perpendicular to each other, and both are perpendicular to the direction of the wave's movement.
- Electromagnetic radiation behaves like waves and travels at the speed of light.
- These waves are known as electromagnetic waves or electromagnetic radiation.
- They do not require a material medium to propagate.
Electromagnetic Wave
- Light waves are electromagnetic waves which do not require a material medium for their propagation.
- Due to transverse nature, light wave undergo polarisation.
- The velocity of electromagnetic wave in vacuum is c = 1 / √μo εo.
- The velocity of electromagnetic waves in medium is less than that of light, v < c
v = 1 / √μo εo εr μr = c / √μo εr
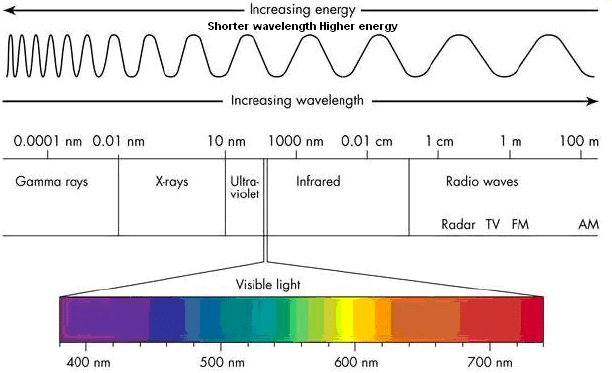 Electromagnetic Spectrum
Electromagnetic Spectrum
- The velocity of electromagnetic waves in a medium depends upon the electric and magnetic properties of the medium.
where, μo = absolute magnetic permeability and εo = absolute electrical permittivity of free space.
The wave theory is not sufficient alone without quantum mechanics to explain the phenomenon of photoelectric effect, Compton effect and Raman effect.
Max Planck’s Quantum Theory
 Max Planck
Max Planck
- Light emits from a source in the form of packets of energy called quanta or photons.
- The energy of a photon is E = hv, where h is Planck’s constant and v is the frequency of light.
- Quantum theory could explain photoelectric effect, Compton effect and Raman effect.
- It failed to explain interference, diffraction and polarization of light.
De – Broglie’s Dual Theory

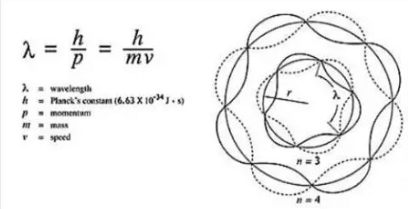
- Light waves have dual nature, wave nature according to Maxwell’s electromagnetic wave theory and particle nature according to Max-Planck’s quantum theory.
- Energy of photon = hv = hc / λ
where, h = Planck’s constant ( 6.626 × 10 -34 m2kg/s) - De-Broglie wave equation is λ = h / p = h / mv
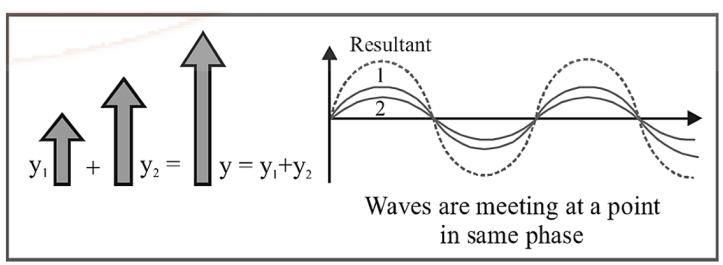
Superposition of Waves
When two similar waves propagate in a medium simultaneously, then at any point the resultant displacement is equal to the vector sum of displacement produced by individual waves.
y = y1 + y2
Graphical View
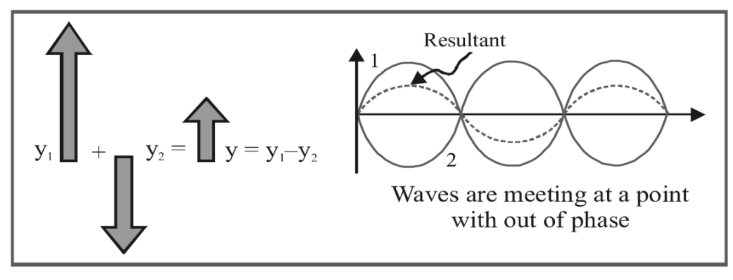
- Phase: Phase refers to the argument of the sine or cosine function in a wave's displacement equation. For the equation represents the phase or instantaneous phase.
- Phase Difference (): Phase difference is the variation between the phases of two waves at a specific point. For example, if and , then the phase difference is .
- Path Difference (): Path difference is the discrepancy in the lengths of two waves travelling to a meeting point. It can be expressed as .
- Resultant amplitude and intensity: If we have two waves represented by the equations y1=a1sin(ωt) and y2=a2 sin(ωt+ϕ), where a1 and a2 are the individual amplitudes, and ϕ represents the phase difference when they meet at a point, the intensities of the waves are denoted as I1 and I2.
(i) Resultant Amplitude: The resultant amplitude (or the amplitude of the combined wave) after superimposing the two waves is given by:
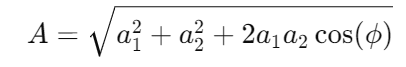 For the specific case where the phase difference is 90°, the resultant amplitude can be simplified to:
For the specific case where the phase difference is 90°, the resultant amplitude can be simplified to: 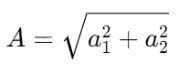
(ii) Resultant Intensity: Intensity is proportional to the square of the amplitude, expressed as 𝐼 ∝ 𝐴2. Therefore, using the amplitudes, we can derive the formula for resultant intensity as:
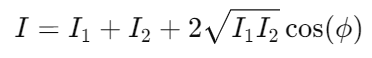
The term 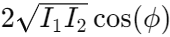 is known as the interference term. In cases of incoherent interference, this term is zero, leading to the resultant intensity simply being:
is known as the interference term. In cases of incoherent interference, this term is zero, leading to the resultant intensity simply being:
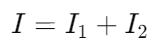
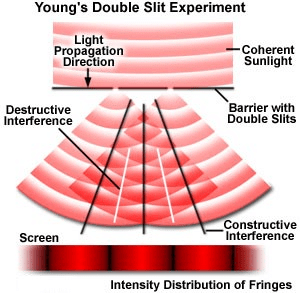
Interference of Light
- When two light waves of similar frequency having a zero or constant phase difference propagate in a medium simultaneously in the same direction, then due to their superposition, maximum intensity occurs at points of constructive interference and minimum intensity at points of destructive interference.
- This phenomena of energy redistribution due to superposition of waves is called interference of light waves.
Fringe Width
The distance between the centers of two consecutive bright or dark fringes is called the fringe width.
The angular fringe width is given by θ = λ / d, where λ is the wavelength of light d is the distance between two coherent sources.
Types of Interference:

Resultant intensity due to two identical waves
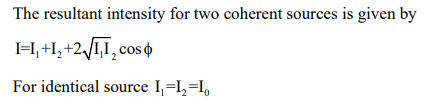
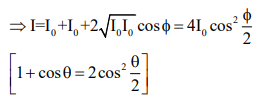
Coherent Sources of Light
The sources of light emitting light of the same wavelength, the same frequency having a zero or constant phase difference are called coherent sources of light.
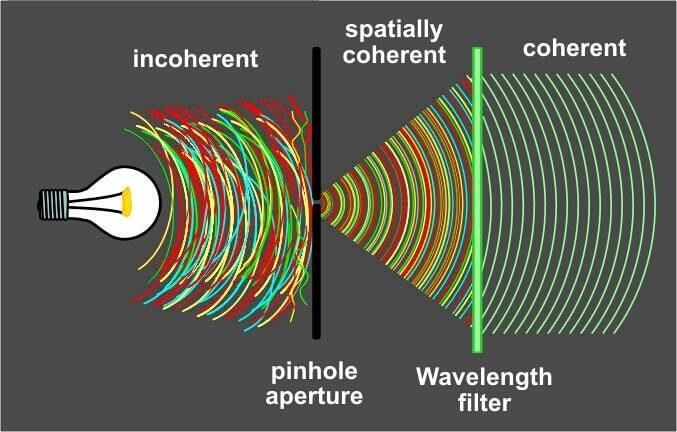 Coherent source of light
Coherent source of light
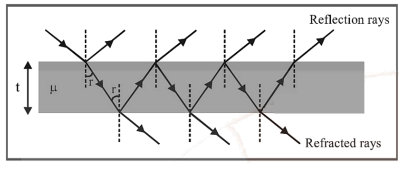
When a transparent sheet of refractive index μ and of thickness t is introduced in one of the path of interfering waves, then fringe pattern shifts in that direction by a distance Y
Y = D / d (μ – 1) t = β / λ (μ – 1) t
where, β = fringe width.
Illustrations of Interference
Interference effects are frequently seen in thin films when their thickness is similar to the wavelength of the incoming light.
- If the film is very thin compared to the wavelength, it appears dark;
- If it's too thick, it appears uniformly illuminated.
- For example, a thin layer of oil on water or soap bubbles displays various colors in white light due to the interference of waves reflected from the film's two surfaces.
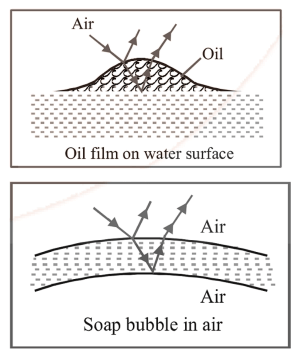
Thin Films
In thin films, interference occurs between the waves reflected from both surfaces of the film and those refracted through it.
Llyod’s Mirror
- A glass plate acts as a mirror, creating a virtual image of a light source ( real source) . Both the source and its virtual image act as coherent sources, similar to a double-slit experiment.
- The key difference is a 180° phase shift during reflection, which makes dark fringes appear where you'd expect bright ones.
- If the path difference between the direct and reflected waves equals a whole number of wavelengths, the point appears dark (not bright).
- Fringe conditions:
Minima (dark): Δx = (2n - 1)λ/2
Maxima (bright): Δx = nλ
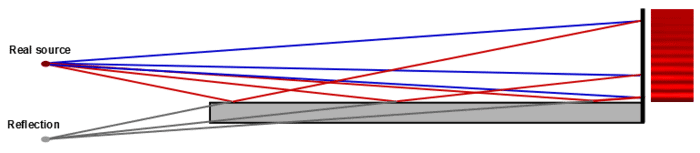 Llyod's Mirror
Llyod's Mirror
Reflection changes the usual interference pattern by altering where dark and bright fringes appear.
Doppler's Effect in Light
The change in frequency (or wavelength) of light caused by the relative motion between the light source and the observer is known as Doppler's Effect.
According to the special theory of relativity, the relationship between the actual frequency (𝑣) and the apparent frequency (𝑣′ ) can be expressed as:
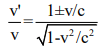
where,
𝑣= actual frequency of the light
𝑣′= apparent frequency observed
𝑣 = speed of the source relative to a stationary observer
𝑐 = speed of light

Applications of Doppler's Effect in Light
|
74 videos|314 docs|88 tests
|
FAQs on Introduction to Wave Optics - Physics Class 12 - NEET
| 1. What is Huygen’s Principle and how is it applied in wave optics? |  |
| 2. How does the Doppler Effect apply to light and what are its implications? |  |
| 3. What is the significance of interference of light in wave optics? |  |
| 4. Can you explain Lloyd’s Mirror and its application in wave optics? |  |
| 5. How does Maxwell’s electromagnetic wave theory relate to wave optics? |  |
















