Irodov Solutions: Hydrodynamics | Physics Class 11 - NEET PDF Download
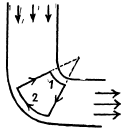
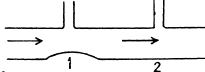
Q. 315. Ideal fluid flows along a flat tube of constant cross-section, located in a horizontal plane and bent as shown in Fig. 1.80 (top view). The flow is steady. Are the pressures and velocities of the fluid equal at points 1 and 2? What is the shape of the streamlines?
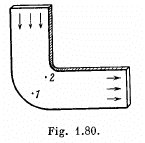
Solution. 315. Between 1 and 2 fluid particles are in nearly circular motion and therefore have centripetal acceleration. The force for this acceleration, like for any other situation in an ideal fluid, can only come from the pressure variation along the line joining 1 and 2. This requires that pressure at 1 should be greater than the pressure at 2 i.e.
P1 > P2
so that the fluid particles can have required acceleration. If there is no turbulence, the motion can be taken as irrotational. Then by considering
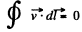
along the circuit shown we infer that
(The portion of the circuit near 1 and 2 are streamlines while the other two arms are at right angle to streamlines)
In an incompressible liquid we also have div 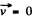
By electrostatic analogy we then find that the density of streamlines is proportional to the velocity at that point.
Q. 316. Two manometric tubes are mounted on a horizontal pipe of varying cross-section at the sections S1 and S2 (Fig. 1.81). Find the volume of water flowing across the pipe's section per unit time if the difference in water columns is equal to Δh.
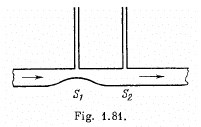
Solution. 316. From the conservation of mass
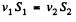 (1)
(1)
But S1 < S2 as shown in the figure of the problem, therefore
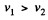
As every streamline is horizontal between 1 & 2, Bemoull’s theorem becomes
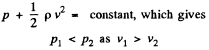
As the difference in height o f the water column is Δh , therefore
 (2)
(2)
From Bernoulli theorem between points 1 and 2 of a streamline
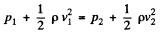
or, 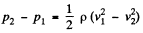
or 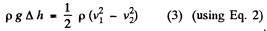
using (1) in (3), we get
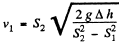
Hence the sought volume of water flowing per see
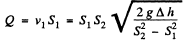
Q. 317. A Pitot tube (Fig. 1.82) is mounted along the axis of a gas pipeline whose cross-sectional area is equal to S. Assuming the viscosity to be negligible, find the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquid and the gas are P0 and p respectively;
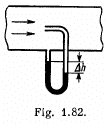
Solution. 317. Applying Bernoulli’s theorem for the point A and B,
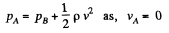
or, 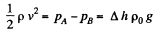
So, 
Thus, rate of flow of gas, 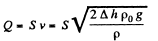

The gas flows over the tube past it at B. But at A the gas becomes stationary as the gas will move into the tube which already contains gas.
In applying Bernoulli’s theorem we should remember that 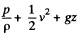 is constant along a streamline. In the present case, we are really applying Bernoulli's theorem somewhat indirectly. The streamline at A is not the streamline at B. Nevertheless the result is correct. To be convinced of this, we need only apply Bernoulli theorem to the streamline that goes through A by comparing the situation at A with that above B on the same level. In steady conditions, this agrees with the result derived because there cannot be a transverse pressure differential.
is constant along a streamline. In the present case, we are really applying Bernoulli's theorem somewhat indirectly. The streamline at A is not the streamline at B. Nevertheless the result is correct. To be convinced of this, we need only apply Bernoulli theorem to the streamline that goes through A by comparing the situation at A with that above B on the same level. In steady conditions, this agrees with the result derived because there cannot be a transverse pressure differential.
Q. 318. A wide vessel with a small hole in the bottom is filled with water and kerosene. Neglecting the viscosity, find the velocity of the water flow, if the thickness of the water layer is equal to h1 = 30 cm and that of the kerosene layer to h2 = 20 cm.
Solution. 318. Since, the density of water is greater than that of kerosene oil, it will collect at the bottom. Now, pressure due to water level equals h1 p1 g and pressure due to kerosene oil level equals h2 p2 g. So, net pressure becomes h1 p1 g + h2 p2 g.
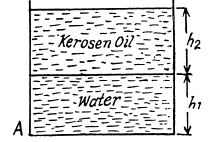
From Bernoulli’s theorem, this pressure energy will be converted into kinetic energy while flowing through the whole A.
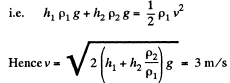
Q. 319. A wide cylindrical vessel 50 cm in height is filled with water and rests on a table. Assuming the viscosity to be negligible, find at what height from the bottom of the vessel a small hole should be perforated for the water jet coming out of it to hit the surface of the table at the maximum distance lmax from the vessel. Find lmax.
Solution. 319. Let, H be the total height of water column and the hole is made at a height h from the bottom.
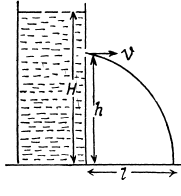
Then from Bernoulli’s theorem
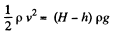
or,  which is directed h orizontally.
which is directed h orizontally.
For the horizontal range, l = v t
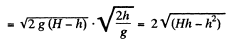
Now, for maximum 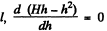
which yields 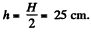
Q. 320. A bent tube is lowered into a water stream as shown in Fig. 1.83. The velocity of the stream relative to the tube is equal to v = 2.5 m/s. The closed upper end of the tube located at the height 12, h0 = 12 cm has a small orifice. To what height h will the water jet spurt?
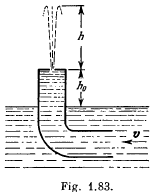
Solution. 320. Let the velocity of the water jet, near the orifice be v', then applying Bemoullis theorem,
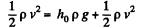
or, 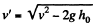 (1)
(1)
Here the pressure term on both sides is the same and equal to atmospheric pressure. (In the problem book Fig. should be more clear.)
Now, if it rises upto a height h, then at this height, whole of its kinetic energy will be converted into potential energy. So,
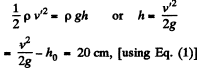
Q. 321. The horizontal bottom of a wide vessel with an ideal fluid has a round orifice of radius R1 over which a round closed cylinder is mounted, whose radius R2 > R1 ( Fig. 1.84). The clearance between the cylinder and the bottom of the vessel is very small, the fluid density is p. Find the static pressure of the fluid in the clearance as a function of the distance r from the axis of the orifice (and the cylinder), if the height of the fluid is equal to h.
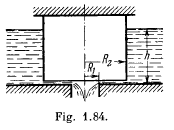
Solution. 321. Water flows through the small clearance into the orifice. Let d be the clearance. Then from the equation of continuity
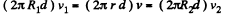
or 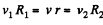 (1)
(1)
where v1, v2 and v are respectively the inward radial velocities of the fluid at 1, 2 and 3.
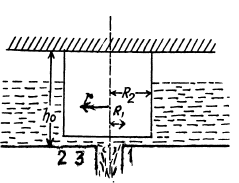
Now by Bernoulli's theorem just before 2 and just after it in the clearance
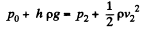 (2)
(2)
Applying the same theorem at 3 and 1 we find that this also equals
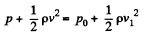 (3)
(3)
(since the pressure in the orifice is p0)
From Eqs. (2) and (3) we also hence
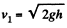 (4)
(4)
and 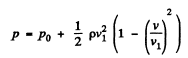
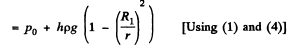
Q. 322. What work should be done in order to squeeze all water from a horizontally located cylinder (Fig. 1.85) during the time t by means of a constant force acting on the piston? The volume of water in the cylinder is equal to V, the cross-sectional area of the ori- fice to s, with s being considerably less than the piston area. The friction and viscosity are negligibly small.
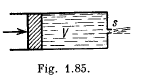
Solution. 322. Let the force acting on the piston he F and foe length oi the cylinder be l.
Then, work done = FI (1)

Applying Bernoulli's theorem for points 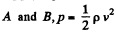 where P is density and v is the velocity at point B. Now, force on the piston,
where P is density and v is the velocity at point B. Now, force on the piston,
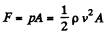 (2)
(2)
where A is the cross section area of piston.
Also, discharge through the orifice during time interval t = Svt and this is equal to the volume of the cylinder, i.e.,
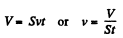 (3)
(3)
From Eq. (1), (2) and (3) work done
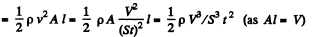
Q. 323. A cylindrical vessel of height h and base area S is filled with water. An orifice of area s ≪ S is opened in the bottom of the vessel. Neglecting the viscosity of water, determine how soon all the water will pour out of the vessel.
Solution. 323. Let at any moment of time, water level in the vessel be H then speed of' flow of water through the orifice, at that moment will be
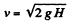 (1)
(1)
In the time interval dt, the volume of water ejected through orifice,
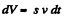 (2)
(2)
On the other hand, the volume of water in the vessel at time t equals
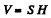
Differentiating (3) with respect to time,
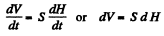 (4)
(4)
Eqs. (2) and (4)
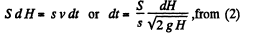
Integrating, 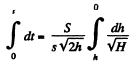
Thus, 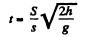
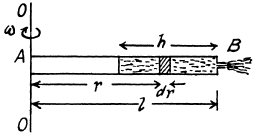
Q. 324. A horizontally oriented tube AB of length 1 rotates with a constant angular velocity ω about a stationary vertical axis OO' passing through the end A (Fig. 1.86). The tube is filled with an ideal fluid. The end A of the tube is open the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.
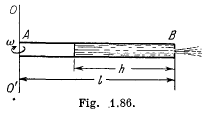
Solution. 324. In a rotating frame (with constant angular velocity) the Eulerian equation is
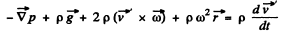
In the frame of rotating tube the liquid in the "column* is practically static because the orifice is sufficiently small. Thus the Eulerian Eq. in projection form along 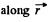 (which is the position vector of an arbitrary liquid element of lenth dr relative to the rotation axis reduces to
(which is the position vector of an arbitrary liquid element of lenth dr relative to the rotation axis reduces to
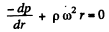
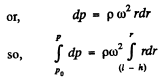
Thus 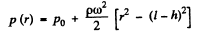 (1)
(1)
Hence the pressure at the end B just before the orifice i.e.
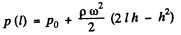 (2)
(2)
Then applying Bemouirs theorem at the orifice for the points just inside and outside of the end B
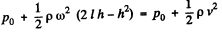 (where v is the sought velocity)
(where v is the sought velocity)
So, 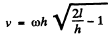
Q. 325. Demonstrate that in the case of a steady flow of an ideal fluid Eq. (1.7a) turns into Bernoulli equation.
Solution. 325. The Euler’s equation 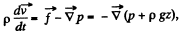 where z is vprtirallv upwards.
where z is vprtirallv upwards.
Now 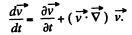 (1)
(1)
But 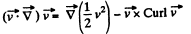 (2)
(2)
we consider the stead 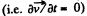 flow of an incompressible fluid then p = constant.
flow of an incompressible fluid then p = constant.
and as the motion is irrotational Curl 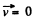
So from (1) and (2) 
or, 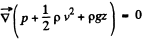
Hence 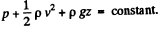
Q. 326. On the opposite sides of a wide vertical vessel filled with water two identical holes are opened, each having the cross-sectional area S = 0.50 cm2. The height difference between them is equal to Δh = 51 cm. Find the resultant force of reaction of the water flowing out of the vessel.
Solution. 326. Let the velocity of water, flowing through A be vA and that through B be vB, then discharging rate through A = QA = S vA and similarly through B = S vB.
Now, force of reaction at A,
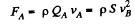
Hence, the net force,
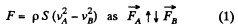
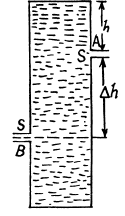
Applying Bernoulli’s theorem to the liquid flowing out of A we get
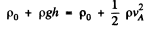
and similarly at B
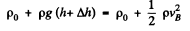
Hence 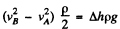
Thus 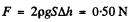
Q. 327. The side wall of a wide vertical cylindrical vessel of height h = 75 cm has a narrow vertical slit running all the way down to the bottom of the vessel. The length of the slit is l = 50 cm and the width b = 1.0 mm. With the slit closed, the vessel is filled with water. Find the resultant force of reaction of the water flowing out of the vessel immediately after the slit is opened.
Solution. 327. Consider an element of height dy at a distance y from the top. The velocity of the fluid coming out of the element is
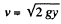
The force of reaction dF due to this is 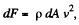 as in the previous problem,
as in the previous problem, 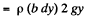
Integrating 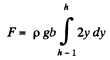
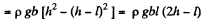
(The slit runs from a depth h - l to a depth h from the top.)
Q.328. Water flows out of a big tank along a tube bent at right angles: the inside radius of the tube is equal to r = 0.50 cm (Fig. 1.87). The length of the horizontal section of the tube is equal to l = 22 cm. The water flow rate is Q = 0.50 litres per second. Find the moment of reaction forces of flowing water, acting on the tube's walls, relative to the point O.
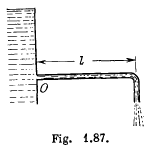
Solution. 328. Let the velocity of water flowing through the tube at a certain instant of time be u, then 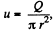 where Q is the rate of flow of water and πr2 is the cross section area of the tube.
where Q is the rate of flow of water and πr2 is the cross section area of the tube.
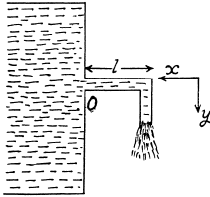
From impulse momentum theorem, for the stream of water striking the tube comer, in x-direction in the time interval dt,
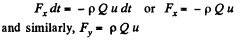
Therefore, the force exerted on the water stream by the tube,
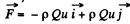
According to third law, the reaction force on the tube’s wall by the stream equals 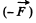
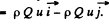
Hence, the sought moment of force about 0 becomes
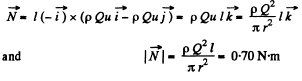
Q.329. A side wall of a wide open tank is provided with a narrowing tube (Fig. 1.88) through which water flows out. The cross-sectional area of the tube decreases from S = 3.0 cm2 to s = 1.0 cm2. The water level in the tank is h = 4.6 m higher than that in the tube. Neglecting the viscosity of the water, find the horizontal component of the force tending to pull the tube out of the tank.
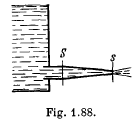
Solution. 329. Suppose the radius at A is R and it decreases uniformaly to r at B where S = πR2 and s = πr2. Assume also that the semi vectical angle at 0 is α. Then
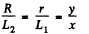
So 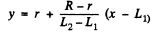
where y is the radius at the point P distant x from the vertex O. Suppose the velocity with which the liquid flows out is V at A, v at B and u at P. Then by the equation of continuity
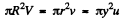
The velocity v of efflux is given by
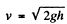
and Bernoulli's theorem gives
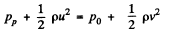
where pp is the pressure at P and p0 is the atmospheric pressure which is the pressure just outside of B. The force on the nozzle tending to pull it out is then
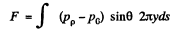
We have subtracted p0 which is the force due to atmosphenic pressure the factor sinθ gives horizontal component of the force and ds is the length of the element of nozzle surface, ds = dx sec θ and

Thus

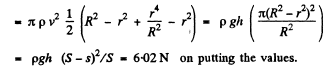
Note : If we try to calculate F from the momentum change of the liquid flowing out will be wrong even as regards the sign of the force.
There is of course the effect of pressure at S and s but quantitative derivation of F fron Newton's law is difficult.
Q.330. A cylindrical vessel with water is rotated about its vertical axis with a constant angular velocity ω. Find:
(a) the shape of the free surface of the water;
(b) the water pressure distribution over the bottom of the vessel along its radius provided the pressure at the central point is equal to Po.
Solution. 330. The Euler’s equation is 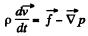 in the space fixed frame where
in the space fixed frame where 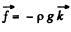 downward. We assume incompressible fluid so p is constant.
downward. We assume incompressible fluid so p is constant.
Then 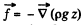 where z is the height vertically upwards from some fixed origin. We go to rotating frame where the equation becomes
where z is the height vertically upwards from some fixed origin. We go to rotating frame where the equation becomes
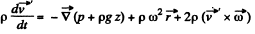
the additional terms on the right are the well known coriolis and centrifugal forces. In the frame rotating with the liquid 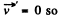
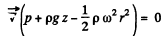
or 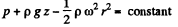
On the free surface p = constant, thus

If we choose the origin at point r = 0 fi.e. the axis) of the free surface then “cosntant” = 0 and
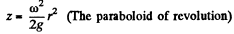
At the bottom z = constant
So 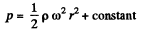
If p = p0 on the axis at the bottom, then
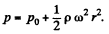
Q.331. A thin horizontal disc of radius R = 10 cm is located within a cylindrical cavity filled with oil whose viscosity η = 0.08 P (Fig. 1.89). The clearance between the disc and the horizontal planes of the cavity is equal to h = 1.0 mm. Find the power developed by the viscous forces acting on the disc when it rotates with the angular velocity ω = 60 rad/s. The end effects are to be neglected.
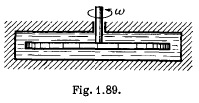
Solution. 331. When the disc rotates the fuild in contact with, corotates but the fluid in contact with the walls of the cavity does not rotate. A velocity gradient is then set up leading to viscous forces. At a distance r from the axis the linear velocity is ω r so there is a velocity gradient 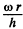 both in the upper and lower clearance. The corresponding force on the element whose radial width is dr is
both in the upper and lower clearance. The corresponding force on the element whose radial width is dr is
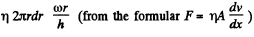
The torque due to this force is

2nd the net torque considering both the upper and lower clearance is
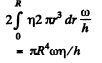
So power developed is
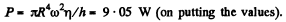
(A s instructed end effects i.e. rotation of fluid in the clearance r > R has been neglected.)
Q.332. A long cylinder of radius R1 is displaced along its axis with a constant velocity v0 inside a stationary co-axial cylinder of radius R2. The space between the cylinders is filled with viscous liquid. Find the velocity of the liquid as a function of the distance r from the axis of the cylinders. The flow is laminar.
Solution. 332. Let us consider a coaxial cylinder of radius r and thickness dr. then force of friction or viscous force on this elemental layer 
This force must be constant from layer to layer so that steady motion may be possible.
or, 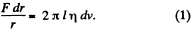
Integrating, 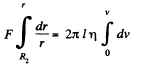
or, 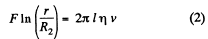

Putting
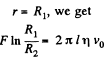
From (2) by (3) we get,
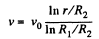
Note : The force F is supplied by the agency which tries to carry the inner cylinder with velocity v0.
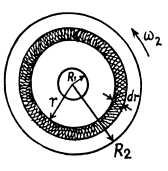
Q.333. A fluid with viscosity η fills the space between two long co-axial cylinders of radii R1 and R2, with R1 < R2. The inner cylinder is stationary while the outer one is rotated with a constant angular velocity ω2. The fluid flow is laminar. Taking into account that the friction force acting on a unit area of a cylindrical surface of radius r is defined by the formula 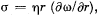 find:
find:
(a) the angular velocity of the rotating fluid as a function of radius r;
(b) the moment of the friction forces acting on a unit length of the outer cylinder.
Solution. 333. (a) Let us consider an elemental cylinder of radius r and thickness dr then from Newton’s formula
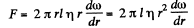
and moment of this force acting on the element,
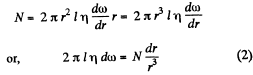
As in the previous problem N is constant when conditions are steady
Integrating, 
or, 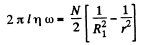 (3)
(3)
Putting 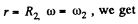

From (3) and (4),
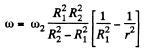
(b) From Eq. (4),
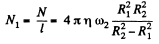
Q.334. A tube of length 1 and radius R carries a steady flow of fluid whose density is p and viscosity η. The fluid flow velocity de- pends on the distance r from the axis of the tube as 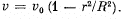 Find:
Find:
(a) the volume of the fluid flowing across the section of the tube per unit time;
(b) the kinetic energy of the fluid within the tube's volume;
(c) the friction force exerted on the tube by the fluid;
(d) the pressure difference at the ends of the tube.
Solution. 334. (a) Let dV be the volume flowing per second through the cylindrical shell of thickness dr then,
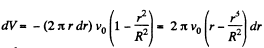
and the total volume,
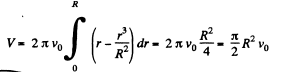

(b) Let, dE be the kinetic energy, within the above cylindrical shell. Then
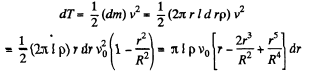
Hence, total energy of the fluid,
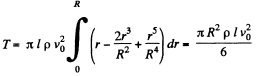
(c) Here frictional force is the shearing force on the tube, exerted by the fluid, which equals 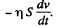
Given, 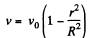
So, 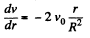
And at 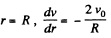
Then, viscous force is given by, 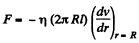

(d) Taking a cylindrical shell of thickness dr and radius r viscous force,
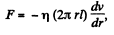
Let Δp be the pressure difference, then net force on the element 
But, since the flow is steady, 
or, 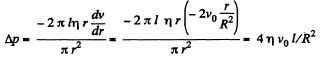
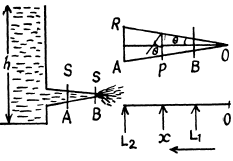
Q.335. In the arrangement shown in Fig. 1.90 a viscous liquid whose density is p = 1.0 g/cm3 flows along a tube out of a wide tank A. Find the velocity of the liquid flow, if h1 = 10 cm, h2 = 20 cm, and h3 = 35 cm. All the distances l are equal.
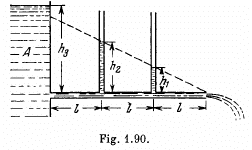
Solution. 335. The loss of pressure head in travelling a distance l is seen from the middle section to be h2 - h1 = 10 cm. Since h2 - h1 = h1 in our problem and h3 - h2 = 15 cm = 5 + h2 h1, we see that a pressure head of 5 cm remains incompensated and must be converted into kinetic energy, the liquid flowing out. Thus

Thus 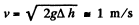
Q.336. The cross-sectional radius of a pipeline decreases gradually as 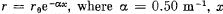 is the distance from the pipeline inlet. Find the ratio of Reynolds numbers for two cross-sections separated by Δx = 3.2 m.
is the distance from the pipeline inlet. Find the ratio of Reynolds numbers for two cross-sections separated by Δx = 3.2 m.
Solution. 336. We know that, Reynold’s number (Re) is defined as, 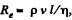 where v is the velocity / is the characteristic length and r\ the coefficient of viscosity. In the case of circular cross section the chracteristic length is the diameter of cross-section d, and v is taken as average velocity of flow of liquid.
where v is the velocity / is the characteristic length and r\ the coefficient of viscosity. In the case of circular cross section the chracteristic length is the diameter of cross-section d, and v is taken as average velocity of flow of liquid.
Now,  (Reynold’s number at x1 from the pipe end)
(Reynold’s number at x1 from the pipe end) 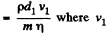 is the velocity at distance x1
is the velocity at distance x1
and similarly, 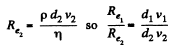
From equation of continuity, 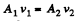
or, 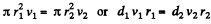
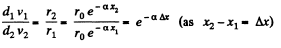
Thus 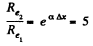
Q.337. When a sphere of radius r1 = 1.2 mm moves in glycerin, the laminar flow is observed if the velocity of the sphere does not exceed v1 = 23 cm/s. At what minimum velocity v2 of a sphere of radius r2 = 5.5 cm will the flow in water become turbulent? The viscosities of glycerin and water are equal to η1 = 13.9 P and η2 = 0.011 P respectively.
Solution. 337. We know that Reynold’s number for turbulent flow is greater than that on laminar flow.
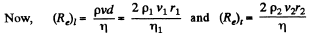
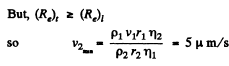 on putting the values.
on putting the values.
Q.338. A lead sphere is steadily sinking in glycerin whose viscosity is equal to η = 13.9 P. What is the maximum diameter of the sphere at which the flow around that sphere still remains laminar? It is known that the transition to the turbulent flow corresponds to Reynolds number Re = 0.5. (Here the characteristic length is taken to be the sphere diameter.)
Solution. 338. 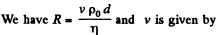
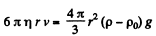
(p = density of lead, p0 = density of glycerine.)
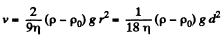
Thus 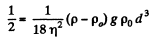
and 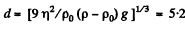 mm on putting the values,
mm on putting the values,
Q.339. A steel ball of diameter d = 3.0 mm starts sinking with zero initial velocity in olive oil whose viscosity is η = 0.90 P. How soon after the beginning of motion will the velocity of the ball differ from the steady-state velocity by n = 1.0%?
Solution. 339. 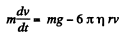
or 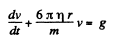
or 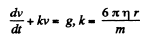
or 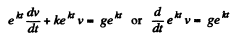
or 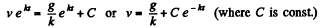
Since 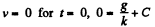
So 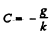
Thus 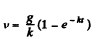
The steady state velocity is g/k.
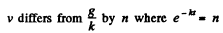
or 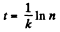
Thus 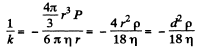
We have neglected buoyancy in olive oil.
|
96 videos|367 docs|98 tests
|
FAQs on Irodov Solutions: Hydrodynamics - Physics Class 11 - NEET
| 1. What is hydrodynamics and why is it important in physics? |  |
| 2. What are some practical applications of hydrodynamics? |  |
| 3. How can the Bernoulli's principle be applied in hydrodynamics? |  |
| 4. What are some fundamental equations used in hydrodynamics? |  |
| 5. How does hydrodynamics relate to the study of waves and tides? |  |

















