Hydrogen Atom Wave Functions and Quantum Numbers | Chemistry Optional Notes for UPSC PDF Download
Introduction
- The hydrogen atom, consisting of an electron and a proton, is a two-particle system, and the internal motion of two particles around their center of mass is equivalent to the motion of a single particle with a reduced mass. This reduced particle is located at r, where r is the vector specifying the position of the electron relative to the position of the proton.
- The length of r is the distance between the proton and the electron, and the direction of r and the direction of r is given by the orientation of the vector pointing from the proton to the electron. Since the proton is much more massive than the electron, we will assume throughout this chapter that the reduced mass equals the electron mass and the proton is located at the center of mass.
 Figure 4.10.1: a) The proton ( p+) and electron (e−) of the hydrogen atom. b) Equivalent reduced particle with reduced mass μ at distance r from center of mass.
Figure 4.10.1: a) The proton ( p+) and electron (e−) of the hydrogen atom. b) Equivalent reduced particle with reduced mass μ at distance r from center of mass.
Since the internal motion of any two-particle system can be represented by the motion of a single particle with a reduced mass, the description of the hydrogen atom has much in common with the description of a diatomic molecule discussed previously. The Schrödinger Equation for the hydrogen atom (4.10.1)
(4.10.1)
employs the same kinetic energy operator, , written in spherical coordinates. For the hydrogen atom, however, the distance, r, between the two particles can vary, unlike the diatomic molecule where the bond length was fixed, and the rigid rotor model was used. The hydrogen atom Hamiltonian also contains a potential energy term,
, written in spherical coordinates. For the hydrogen atom, however, the distance, r, between the two particles can vary, unlike the diatomic molecule where the bond length was fixed, and the rigid rotor model was used. The hydrogen atom Hamiltonian also contains a potential energy term,  , to describe the attraction between the proton and the electron. This term is the Coulomb potential energy,
, to describe the attraction between the proton and the electron. This term is the Coulomb potential energy,  (4.10.2)
(4.10.2)
where r is the distance between the electron and the proton. The Coulomb potential energy depends inversely on the distance between the electron and the nucleus and does not depend on any angles. Such a potential is called a central potential. It is convenient to switch from Cartesian coordinates x, y, z to spherical coordinates in terms of a radius r, as well as angles ϕ, which is measured from the positive x axis in the xy plane and may be between 0 and 2π, and θ, which is measured from the positive z axis towards the xy plane and may be between 0 and π. The time-indepdent Schrödinger equation (in spherical coordinates) for a electron around a positively charged nucleus is then
The time-indepdent Schrödinger equation (in spherical coordinates) for a electron around a positively charged nucleus is then (4.10.3)
(4.10.3)
- Since the angular momentum operator does not involve the radial variable, r, we can separate variables in Equation 4.10.3 by using a product wavefunction. We know that the eigenfunctions of the angular momentum operator are the Spherical Harmonic functions (Table M4), Y(θ,φ), so a good choice for a product function is
ψ(r,θ,φ) = R(r)Y(θ,φ) (4.10.4) - The Spherical Harmonic Y(θ,φ) functions provide information about where the electron is around the proton, and the radial function R(r) describes how far the electron is away from the proton. A solution for both R(r) and Y(θ,φ) with En that depends on only one quantum number n, although others are required for the proper description of the wavefunction:
 (4.10.5)
(4.10.5)
with n = 1,2,3...∞ - The hydrogen atom wavefunctions, ψ(r,θ,ϕ), are called atomic orbitals. An atomic orbital is a function that describes one electron in an atom. The wavefunction with n = 1, ll = 0 is called the 1s orbital, and an electron that is described by this function is said to be “in” the ls orbital, i.e. have a 1s orbital state. The constraints on n, ll), and ml that are imposed during the solution of the hydrogen atom Schrödinger equation explain why there is a single 1s orbital, why there are three 2p orbitals, five 3d orbitals, etc. We will see when we consider multi-electron atoms, these constraints explain the features of the Periodic Table. In other words, the Periodic Table is a manifestation of the Schrödinger model and the physical constraints imposed to obtain the solutions to the Schrödinger equation for the hydrogen atom.
The Three Quantum Numbers
Schrödinger’s approach requires three quantum numbers (n, l, and ml) to specify a wavefunction for the electron. The quantum numbers provide information about the spatial distribution of an electron. Although n can be any positive integer (NOT zero), only certain values of l and ml are allowed for a given value of \(n).
- The principal quantum number (n): One of three quantum numbers that tells the average relative distance of an electron from the nucleus. indicates the energy of the electron and the average distance of an electron from the nucleus
n = 1,2,3,4,...(4.10.6)
As n increases for a given atom, so does the average distance of an electron from the nucleus. A negatively charged electron that is, on average, closer to the positively charged nucleus is attracted to the nucleus more strongly than an electron that is farther out in space. This means that electrons with higher values of n are easier to remove from an atom. All wave functions that have the same value of n are said to constitute a principal shell. All the wave functions that have the same value of n because those electrons have similar average distances from the nucleus. because those electrons have similar average distances from the nucleus. As you will see, the principal quantum number n corresponds to the n used by Bohr to describe electron orbits and by Rydberg to describe atomic energy levels. - The Azimuthal Quantum Number: The second quantum number is often called the azimuthal quantum number (l). One of three quantum numbers that describes the shape of the region of space occupied by an electron.. The value of l describes the shape of the region of space occupied by the electron. The allowed values of l depend on the value of n and can range from 0 to n − 1:
l = 0, 1,., 2, 3, ..(n−1) (4.10.7)
For example, if n = 1, l can be only 0; if n = 2, l can be 0 or 1; and so forth. For a given atom, all wave functions that have the same values of both n and l form a subshell. A group of wave functions that have the same values of n and l. The regions of space occupied by electrons in the same subshell usually have the same shape, but they are oriented differently in space. - The Magnetic Quantum Number: The third quantum number is the magnetic quantum number (ml). One of three quantum numbers that describe the orientation of the region of space occupied by an electron concerning an applied magnetic field.. The value of ml describes the orientation of the region in space occupied by an electron with respect to an applied magnetic field. The allowed values of ml depend on the value of l: ml can range from −l to l in integral steps:
m = −l, −l + 1,...0,...l−1,l (4.10.8)
For example, if l = 0 , ml can be only 0; if l = 1, ml can be −1, 0, or +1; and if l = 2, ml can be −2, −1, 0, +1, or +2.
Each wave function with an allowed combination of n, l, and ml values describes an atomic orbital A wave function with an allowed combination of n, l and ml quantum numbers., a particular spatial distribution for an electron. For a given set of quantum numbers, each principal shell has a fixed number of subshells, and each subshell has a fixed number of orbitals.
Solved Examples
Example 1: How many subshells and orbitals are contained within the principal shell with n = 4?
Given: value of n
Asked for: number of subshells and orbitals in the principal shell
Strategy:
A Given n = 4, calculate the allowed values of l. From these allowed values, count the number of subshells.
B For each allowed value of l, calculate the allowed values of ml. The sum of the number of orbitals in each subshell is the number of orbitals in the principal shell.
Ans: A We know that l can have all integral values from 0 to n − 1. If n = 4, then l can equal 0, 1, 2, or 3. Because the shell has four values of l, it has four subshells, each of which will contain a different number of orbitals, depending on the allowed values of ml.
B For l = 0, ml can be only 0, and thus the l = 0 subshell has only one orbital. For l = 1, ml can be 0 or ±1; thus the l = 1 subshell has three orbitals. For l = 2, ml can be 0, ±1, or ±2, so there are five orbitals in the l = 2 subshell. The last allowed value of l is l = 3, for which ml can be 0, ±1, ±2, or ±3, resulting in seven orbitals in the l = 3 subshell. The total number of orbitals in the n = 4 principal shell is the sum of the number of orbitals in each subshell and is equal to n2: = 16 orbitals = (4principal shells)2
= 16 orbitals = (4principal shells)2
Example 2: How many subshells and orbitals are in the principal shell with n = 3?
Ans: three subshells; nine orbitals
Rather than specifying all the values of n and l every time we refer to a subshell or an orbital, chemists use an abbreviated system with lowercase letters to denote the value of l for a particular subshell or orbital:

The principal quantum number is named first, followed by the letter s, p, d, or f as appropriate. These orbital designations are derived from corresponding spectroscopic characteristics of lines involving them: sharp, principle, diffuse, and fundamental. A 1s orbital has n = 1 and l = 0; a 2p subshell has n = 2 and l = 1 (and has three 2p orbitals, corresponding to ml = −1, 0, and +1); a 3d subshell has n = 3 and l = 2 (and has five 3d orbitals, corresponding to ml = −2, −1, 0, +1, and +2); and so forth.
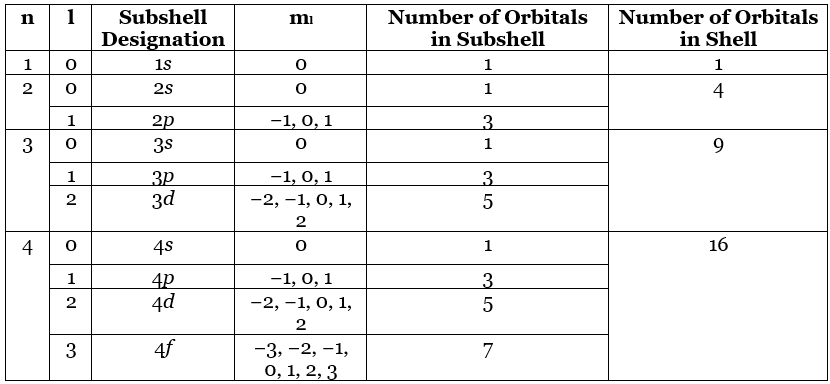
We can summarize the relationships between the quantum numbers and the number of subshells and orbitals as follows (Table 4.10.1):
- Each principal shell has n subshells. For n = 1, only a single subshell is possible (1s); for n = 2, there are two subshells (2s and 2p); for n = 3, there are three subshells (3s, 3p, and 3d); and so forth. Every shell has an ns subshell, any shell with n ≥ 2 also has an np subshell, and any shell with n ≥ 3 also has an nd subshell. Because a 2d subshell would require both n = 2 and l = 2, which is not an allowed value of l for n = 2, a 2d subshell does not exist.
- Each subshell has 2l + 1 orbitals. This means that all ns subshells contain a single s orbital, all np subshells contain three p orbitals, all nd subshells contain five d orbitals, and all nf subshells contain seven f orbitals.
Note: Each principal shell has n subshells, and each subshell has 2l + 1 orbitals.
Table 4.10.1: Allowed values of n, and ml through n = 4
FAQs on Hydrogen Atom Wave Functions and Quantum Numbers - Chemistry Optional Notes for UPSC
| 1. What are the three quantum numbers? |  |
| 2. How do the quantum numbers determine the wave functions of hydrogen atoms? |  |
| 3. What is the significance of the principal quantum number in hydrogen atom wave functions? |  |
| 4. How does the azimuthal quantum number affect the wave functions of hydrogen atoms? |  |
| 5. What is the role of the magnetic quantum number in hydrogen atom wave functions? |  |

 (4.10.5)
(4.10.5)















