Important Derivations: Electric Charges and Fields | Physics Class 12 - NEET PDF Download
Important Derivations
Q1: Using Gauss’s law, prove that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
Sol: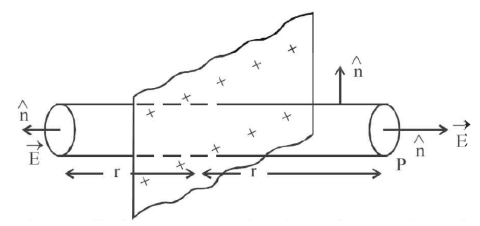
Electric field intensity due to a thin infinite sheet of charge: Let σ be the surface density of charge and P be a point at a distance r from the sheet where  has to be calculated.
has to be calculated.  on either side is perpendicular to the sheet.
on either side is perpendicular to the sheet.
Imagine a cylinder of cross-sectional area ds around P and length 2r, piercing through the sheet. At the two edges, 
At the curved surfaces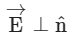 So, there is no contribution to electric flux from the curved surfaces of the cylinder.
So, there is no contribution to electric flux from the curved surfaces of the cylinder.
Electric flux over the edges
Total charge enclosed by the cylinder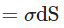 By Gauss’s theorem,
By Gauss’s theorem,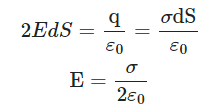 From the expression, it is clear that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
From the expression, it is clear that the electric field at a point due to a uniformly charged infinite plane sheet is independent of the distance from it.
Q2: Derive an expression for the torque experienced by an electric dipole kept in a uniform electric field.
Sol: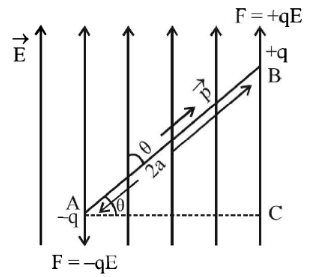
Let the dipole moment 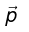 makes an angle θ with the direction of
makes an angle θ with the direction of 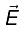
Force on the charge -q = -qE
Force on the charge q = +qE
These forces are equal in magnitude but act along parallel lines at different points hence form a couple which tends to rotate the dipole in the anticlockwise direction.
As, torque = moment of force.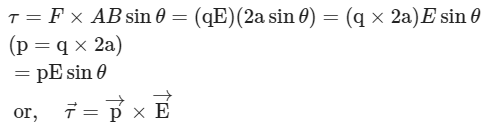
Q3: Derive an expression for the electric field due to an infinitely long straight wire of linear charge density λ C/m.
Sol:
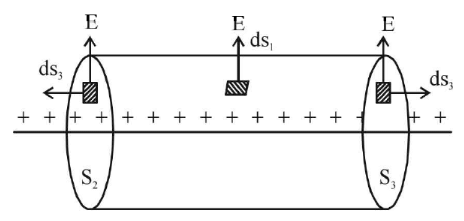
Electric field due to an infinitely long straight wire:
Consider an infinitely long line charge having linear charge density λ. To determine its electric field at distance $r$, consider a cylindrical Gaussian surface of radius r and length ℓ coaxial with the charge. By symmetry, the electric field E has same magnitude at each point of the curved surface S1 and is directed radially outward.
Total flux through the cylindrical surface,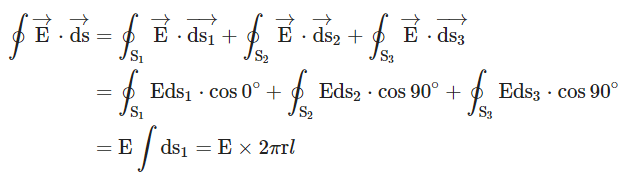 As λ is the charge per unit length and ℓ is the length of the wire,
As λ is the charge per unit length and ℓ is the length of the wire,
so charge enclosed,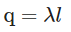 By Gauss’s theorem,
By Gauss’s theorem,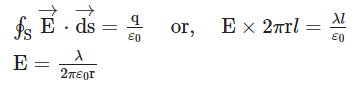 Q4: Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
Q4: Derive the expression for the electric field of a dipole at a point on the equatorial plane of the dipole.
Electric field intensity at point P due to +q (at B)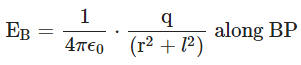
Electric field intensity at P due to q charge (at A )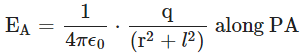
Clearly, 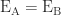 in magnitude.
in magnitude.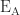 and
and 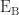 can be resolved into two rectangular components.
can be resolved into two rectangular components.
Components of  (i)
(i) 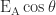 along PX
along PX
(ii) 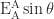 along PY
along PY
Components of EB
(i) 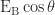 along PX
along PX
(ii) 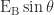 along YP
along YP
Vertical components being equal and opposite cancel each other. Therefore, net electric field intensity along PX 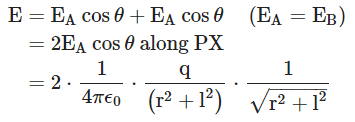 or,
or,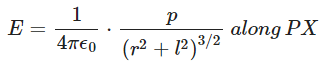
 If l << r so that it can be neglected, then
If l << r so that it can be neglected, then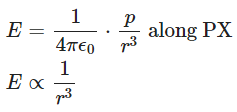 Q5: A dipole, with a dipole moment of magnitude p, is in stable equilibrium in an electrostatic field of magnitude E. Find the work done in rotating this dipole to its position of unstable equilibrium.
Q5: A dipole, with a dipole moment of magnitude p, is in stable equilibrium in an electrostatic field of magnitude E. Find the work done in rotating this dipole to its position of unstable equilibrium.
Sol:
For stable equilibrium, angle between p and E is 0º
For unstable equilibrium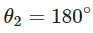 Work done in rotating the dipole from angle θ1 to θ2
Work done in rotating the dipole from angle θ1 to θ2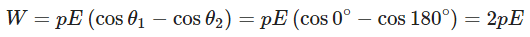
Q6: Deduce the expression for the electric field E due to a system of two charge q1 and q2 with
position vectors r1 and r2 at a point ‘r’ with respect to common origin.
Sol:
Electric field intensity at point P due to q1,
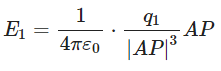 Similarly,
Similarly,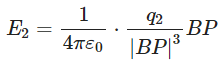 Therefore, Net electric field intensity at point P,
Therefore, Net electric field intensity at point P,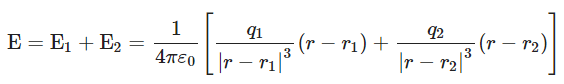
Q7: Two charge –q each are fixed separated by distance 2d. A third charge q of mass m placed at the mid-point is displaced slightly by x (x << d) perpendicular to the line joining the two fixed charged as shown in Fig. Show that q will perform simple harmonic oscillation and also find its time period.
Sol:
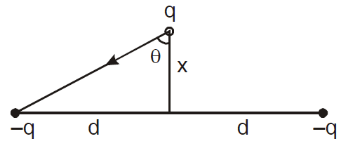
To show that q will perform simple harmonic oscillation and derive the expression for its time period, we can follow these steps: Let the force on charge q due to one of the fixed charges (−q) be F1 and the force due to the other fixed charge be F2. The net force on charge q is given by:
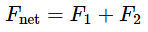
The force between two point charges is given by Coulomb’s Law:
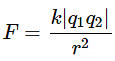
Where k is the Coulomb’s constant, q1 and q2 are the magnitudes of the charges, and r is the separation between the charges. Let the distance of charge q from each of the fixed charges be d. So, the force F1 and F2 can be written as: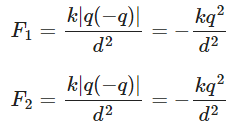 Since both forces are in opposite directions and have the same magnitude, the net force Fnet on charge q will be zero. Now, when charge q is displaced slightly by x in the perpendicular direction (as shown in the figure), the net force Fnet will not remain zero. There will be a restoring force that brings q back to the equilibrium position. The restoring force can be found using Hooke’s Law:
Since both forces are in opposite directions and have the same magnitude, the net force Fnet on charge q will be zero. Now, when charge q is displaced slightly by x in the perpendicular direction (as shown in the figure), the net force Fnet will not remain zero. There will be a restoring force that brings q back to the equilibrium position. The restoring force can be found using Hooke’s Law: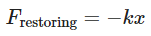 where k is the effective force constant. The effective force constant k can be determined by considering the net force on charge q when it is displaced by x. We can find this by using the concept of superposition:
where k is the effective force constant. The effective force constant k can be determined by considering the net force on charge q when it is displaced by x. We can find this by using the concept of superposition:

Since F1 and F2 were calculated earlier, we can substitute their values: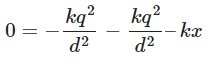 Now, solving for k:
Now, solving for k: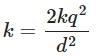
The angular frequency ω of the simple harmonic oscillation can be written as: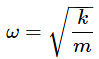
Substitute the value of K: 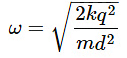
The time period T of the oscillation is given by: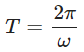
Substitute the value of ω:
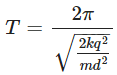
|
88 videos|435 docs|88 tests
|
FAQs on Important Derivations: Electric Charges and Fields - Physics Class 12 - NEET
| 1. What is the formula to calculate the electric field due to a point charge? |  |
| 2. How do you calculate the electric field inside a uniformly charged spherical shell? |  |
| 3. What is the formula to calculate the electric field at a point on the axis of a uniformly charged ring? |  |
| 4. How do you find the electric field at a point due to a uniformly charged infinite line of charge? |  |
| 5. What is Gauss's Law and how is it used to calculate the electric field? |  |
















