Important Questions: Circles | Mathematics (Maths) Class 10 PDF Download
Q1: The maximum number of common tangents that can be drawn to two circles intersecting at two distinct points is:
(a) 4
(b) 3
(c) 2
(d) 1
Ans: (c)
Here, circle with centre O and O' are intersecting at two distinct points A and B. So, in this situation PQ, RS are the tangents which can be drawn.
Q2: In the given figure, O is the centre of the circle. MN is the chord and the tangent ML at point M makes an angle of 70° with MN. The measure of ∠MON is: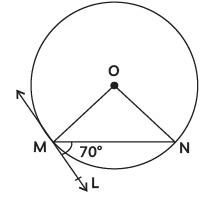
(a) 120º
(b) 140º
(c) 70º
(d) 90º
Ans: (b)
OM ⊥ ML [as tangent from centre is ⊥ at point of contact]∠OML = 90º (∵ The angle between a tangent and a radius at the point of contact is always 90º)and ∠NML = 70º
⇒ ∠OMN + ∠NML = 90º
⇒ ∠OMN = 90º – 70º = 20º
∵ OM = ON = Radii of same circle
∴ ∠OMN = ∠ONM = 20º (Angle opposite to equal sides are equal)
In ∆MON,
∠OMN + ∠ONM + ∠MON = 180º
⇒ 20º + 20º + ∠MON = 180º
⇒ ∠MON = 140º
Q3: In the given figure, if PT is tangent to a circle with centre O and ∠TPO = 35º, then the measure of ∠x is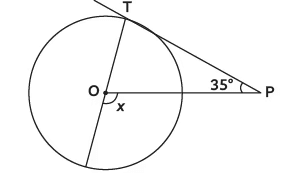 (a) 110º (b) 115º (c) 120º
(a) 110º (b) 115º (c) 120º
(d) 125º
Ans: (d)
∠OTP = 90º [Line from centre is ⊥ to tangent at point of contact] ∠x = ∠TPO + ∠OTP [Exterior Angle Property] x = 35º + 90º = 125º
Q4: In the given figure, PT is a tangent at T to the circle with centre O. If ∠TPO = 25°, then x is equal to:
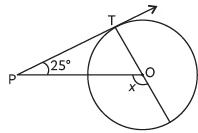 (a) 25°
(a) 25°
(b) 65°
(c) 90°
(d)115°
Ans: (d)
Since tangent is perpendicular to radius at the point of contact.
∴ ∠PTO = 90°
Hence, by the exterior angle formula, in ΔOTP, we get x = 90° + 25°
= 115°
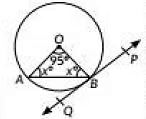
Q5: In the given figure, PQ is tangent to the circle centred at O. If ∠AOB = 95o, then the measure of ∠ABQ will be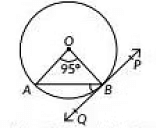 (a) 47.5°
(a) 47.5°
(b) 42.5°
(c) 85°
(d) 95°
Ans: (a)
We have ∠AOB = 95°
In ΔAOB, ∠OAB = ∠OBA (Angle opposite to equal sides are equal)
Now, ∠OAB + 95° + ∠OBA =180° (Angle sum property of a triangle)
= 2∠OAB = 85°∴ ∠OAB = ∠OBA = 42.5° [From (i)]Now, OB is perpendicular to the tangent line PQ
∠OBQ = 90°
∠ABQ + ∠OBA = ∠OBQ = 90°
∠ABQ = 90° - 42.5°
= 47.5°
Q6: In the given figure. TA is tangent to the circle with centre O such that OT = 4 cm, ∠OTA= 30o, then the length of TA is 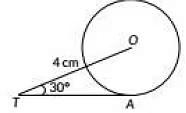 (a) 2√3 cm
(a) 2√3 cm
(b) 2cm
(c) 2√2 cm
(d) √3 cm
Ans: (a)
Draw OA ⊥ TA.In ΔOTA,
∠OAT = 90° [∵ Tangent to a circle is perpendicular to the radius passing through the point of contact]
and ∠OTA = 30°
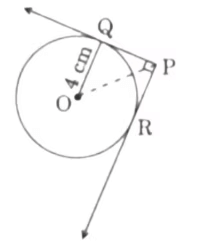
Q7: In the figure, from an external point P, two tangents PQ and PR are drawn to a circle of radius 4 cm with centre O. If ∠QPR= 90°. then the length of PQ is
(a) 3 cm
(b) 4 cm
(c) 2 cm
(d) 2√2 cm
Ans: (b)
Draw a line segment joining the points R and O
Now OQ and OR are equal (Radii of a circle)
∠QPR = 90° (Given)And ∠OQP = ∠ORP = 90° (Tangents make 90 degree angle with radius)
Now, in Quadrilateral PQOR
Sides OQ = OR (Radii)and PR = PQ (Tangents from same point)
And ∠QPR = ∠PRO = ∠PQO = 90°
Therefore, Quadrilateral PQOR is a square.
Since, all sides of a square are equal,
⇒ OR = RP = PQ = OQ = 4 cmHence, length of PQ is 4 cm.
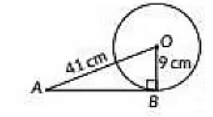
Q8: The length of tangent drawn to a circle of radius 9 cm from a point 41 cm from the centre is
(a) 40 cm
(b) 9 cm
(c) 41 cm
(d) 50 cm
Ans: (a)
OB ⊥ AB [∵As tangent to a circle is perpendicular to the radius through the point of the contact]
In ΔOAB,OA2 = OB2 + AB2 [By Pythagoras theorem]
⇒ (41)2 = 92 + AB2
⇒ AB2 = 412 – 92
= (41 - 9)(41 + 9)
= (32)(50)
= 1600
⇒ AB == 40 cm
Q9: In the given figure. O is the centre of the circle and PQ is the chord. If the tangent PR at P makes an angle of 50° with PQ, then the measure of ∠POQ is (a) 50°
(a) 50°
(b) 40°
(c) 100°
(d) 130°
Ans: (c)
PR is tangent which touches circle at point P.
So, ∠OPR = 90°
∠OPQ = 90° - ∠RPQ = 90° - 50° = 40°
In, ΔPOQ,
OP = OQ (Radii of circle)
So, ∠OQP = ∠OPQ=40°
⇒ ∠POQ = 180° - 40° - 40° = 100°
Q10: Case Study: The discus throw is an event in which an athlete attempts to throw a discus. The athlete spins anti-clockwise around one and a half times through a circle, then releases the throw. When released, the discus travels along the tangent to the circular spin-orbit.
In the given figure, AB is one such tangent to a circle of radius 75cm. Point O is the centre of the circle and ∠ABO = 30°. PQ is parallel to OA.
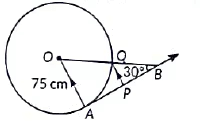
Based on the above information
(a) Find the length of AB.
(b) Find the length of OB.
(c) Find the length of AP.
OR
Find the value of PQ.
Ans:
OR
Q11: Two tangents TP and TQ are drawn to a circle with centre O from an external point T. Prove that ∠PTQ = 2∠OPQ.
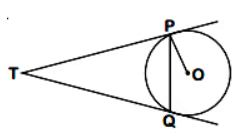
Ans:
We know that the lengths of tangents drawn from an external point to a circle are equal.
∴ TP = TQ ... (1)
∴ ∠TQP = ∠TPQ (angles of equal sides are equal) ... (2)
Now, PT is tangent, and OP is the radius.
∴ OP ⊥ TP (Tangent at any point of a circle is perpendicular to the radius through the point of contact)
∴ ∠OPT = 90°
or, ∠OPQ + ∠TPQ = 90°
or, ∠TPQ = 90° - ∠OPQ ... (3)
In ∆TPQ,
∠TPQ + ∠PQT + ∠QTP = 180° (Sum of angles of a triangle is 180°)
or, 90° - ∠OPQ + ∠TPQ + ∠QTP = 180°
or, 2(90° - ∠OPQ) + ∠TPQ = 180° [from (2) and (3)]
or, 180° - 2∠OPQ + ∠TPQ = 180°
or, 2∠OPQ = ∠TPQ
Hence Proved
Q12: In the given figure, a circle is inscribed in a quadrilateral ABCD in which ∠B = 90°. If AD = 17 cm, AB = 20 cm and DS = 3 cm, then find the radius of the circle.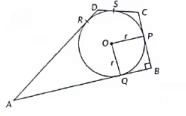
Ans:
Given:
∠B = 90° , AD = 17 cm , AB = 20 cm, DS = 3 cm (where S is the point of tangency on side AD)
From the properties of tangents, we know:
- Tangents drawn from an external point to a circle are equal in length.
- DS = DR (tangents from point D are equal).
- AR = AQ (tangents from point A are equal).
Since AD = 17 cm and DS = 3 cm, we calculate AR as:
- AR = AD - DS = 17 cm - 3 cm = 14 cm
Thus, AR = 14 cm.From the property that AR = AQ, we get:
- AQ = 14 cm.
Since AB = 20 cm and AQ = 14 cm, we calculate BQ as:
- BQ = AB - AQ = 20 cm - 14 cm = 6 cm.
OQ ⊥ BQ and OP ⊥ BP because a tangent at any point of a circle is perpendicular to the radius at the point of contact.
Since both OQ = BQ and the angles between the tangents are 90°, quadrilateral BQOP must be a square.
Since BQ = OQ = r, the radius of the inscribed circle is:
r = 6 cm.
Q13: From an external point, two tangents are drawn to a circle. Prove that the line joining the external point to the centre of the circle bisects the angle between the two tangents.
Ans: Let P lie an external point, O be the centre of the circle and PA and PB are two tangents to the circle as shown in figure.
In ΔOAP and ΔOBP.
OA = OB [Radius of the circle]
OP = OP [common]
PA = PB [∵ Tangents drawn from an external point to a circle are equal]
So, ΔOAP ≅ ΔOPB
So, ∠APO = ∠BPO (By cpct)
Hence. OP bisects ∠APB
Q14: Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Ans: Let the centre of the two concentric circlet is O and AB be the chord of the larger circle which touches the smaller circle at point P as shown in figure.
∴ AB is a tangent to the smaller circle at point P
⇒ OP ⊥ AB
By Pythagoras theorem, in ΔOPAOA2 = AP2 + OP2
⇒ 52 = AP2 +32
⇒ AP2 =52 - 32 = 25 - 9
⇒ AP2 = 16 ⇒ AP = 4cm
In ΔOPB Since, OP ⊥ AB
AP = PB [∵ Perpendicular drawn from the centre of the circle bisects the chord]
∴ AB = 2AP = 2 x 4 = 8 cm
∴ The length of the chord of the larger circle is 8 cm.
Q15: Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line segment joining the points of contact at the centre.
Ans: Let PA and PB are two tangents on a circle from point P as shown in the figure.
Let is known that tangent to a circle is perpendicular to the radius through the point of contact.
∠OAP =∠OBP = 90° ........(i)
In quadrilateral AOBP,
∠OAP + ∠APB + ∠PBO + ∠BOA = 360°
90° + ∠APB + 90° + ∠BOA = 360° [Using (i)]
∠APB + ∠BOA = 360° - 180°
∴ ∠APB + ∠BOA = 180°
Hence proved.
|
127 videos|584 docs|79 tests
|
FAQs on Important Questions: Circles - Mathematics (Maths) Class 10
| 1. What is the definition of a circle in geometry? |  |
| 2. How do you calculate the circumference of a circle? |  |
| 3. What is the area of a circle, and how is it calculated? |  |
| 4. What are the different parts of a circle called? |  |
| 5. How are circles used in real-life applications? |  |