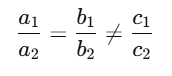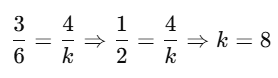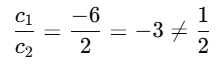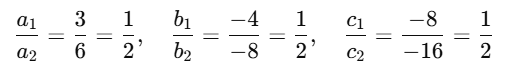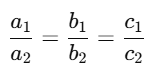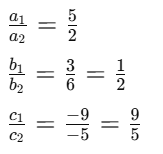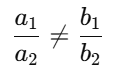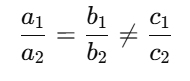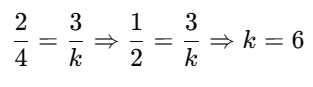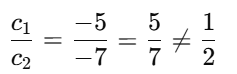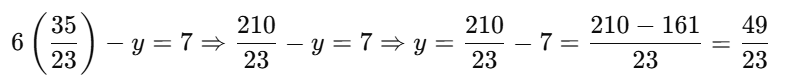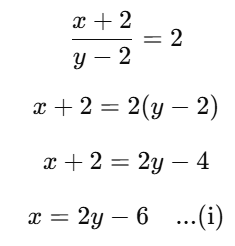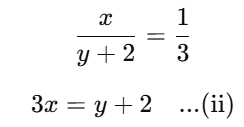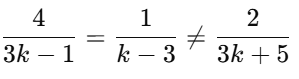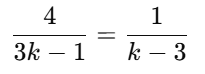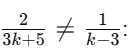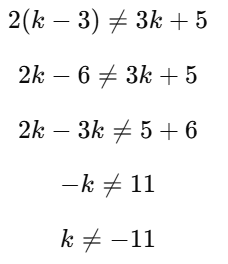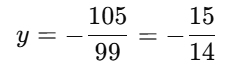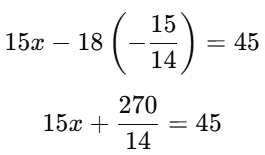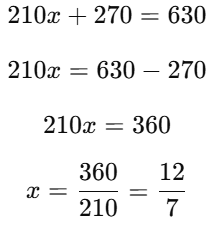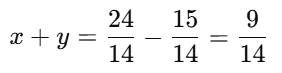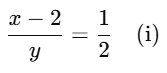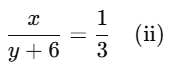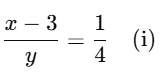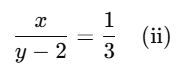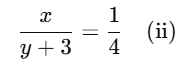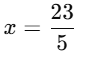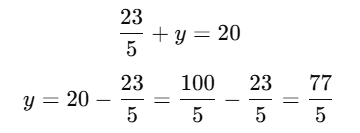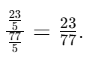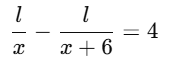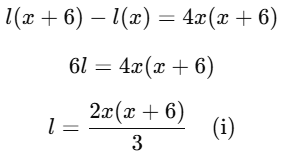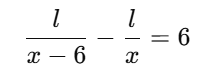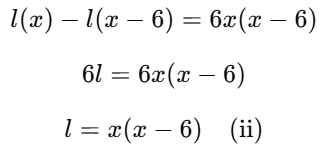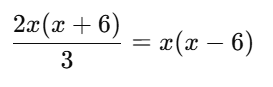Important Questions: Pair of Linear Equations in Two Variables | Mathematics (Maths) Class 10 PDF Download
| Table of contents |

|
| Nature of Solutions of Pair of Linear Equations |

|
| Solving Pair of Linear Equations Algebraically |

|
| Graphical Representation and Solutions |

|
| Applications in Real-World Problems |

|
Nature of Solutions of Pair of Linear Equations
Q1. The pair of linear equations 2x – y + 4 = 0 and –6x = 3y – 10 has:|
(a) a unique solution
(b) exactly two solutions
(c) infinitely many solutions
(d) no solution
Ans: (a)
1st Equation:
2x – y + 4 = 0
→ a₁ = 2, b₁ = –1, c₁ = 4
2nd Equation:
–6x = 3y – 10
→ Rewrite: –6x – 3y + 10 = 0
→ a₂ = –6, b₂ = –3, c₂ = 10
Now compare:
- a1/a2 = 2/(–6) = –1/3
- b1/b2 = –1/(–3) = 1/3
- c1/c2 = 4/10 = 2/5
Here,
a1/a2 ≠ b1/b2,
so the lines intersect at one point, meaning they have a unique solution.
Q2. The value of k for which the pair of linear equations 3x + 4y – 6 = 0 and 6x + ky + 2 = 0 do not have a solution is ______.
(a) 4
(b) 2
(c) 8
(d) 6
Ans: (c)
Given equations:
3x+4y−6=0
→ a1 = 3, b1 = 4, c1 = –6
6x+ky+2=0
→ a2 = 6, b2 = k, c2 = 2
For no solution, the condition is:
Step 1:
Now check:
So, the condition for no solution is satisfied when k = 8
Q3. In the given figure, graphs of two linear equations are shown. The pair of these linear equations is: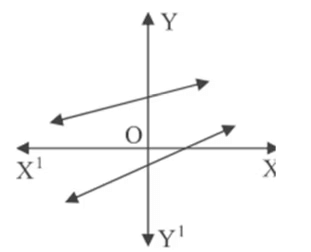
(a) consistent with unique solutions.
(b) consistent with infinitely many solutions.
(c) inconsistent.
(d) inconsistent but can be made consistent by extending these lines.
Ans: (a)
Q4. The pair of linear equations 3x = 4y + 8 and 6x – 8y = 16 represents two lines which are:
(a) intersecting
(b) parallel
(c) coincident
(d) either intersecting or parallel
Ans: (c)
Given:
1. 3x = 4y + 8
→ 3x – 4y – 8 = 02. 6x – 8y = 16
→ Already in standard form
Now, compare:
- a1 = 3, b1 = –4, c1 = –8
- a2 = 6, b2 = –8, c2 = –16
Now check the ratios:
So,
⇒ The pair of lines are coincident.
Q5. The pair of lines represented by the linear equations 5x + 3y = 9 and 2x + 6y – 5 = 0 are:
(a) perpendicular
(b) parallel
(c) intersecting
(d) coincident
Ans: (c)
Given equations: 5x + 3y = 9
→ a1 = 5, b1 = 3, c1 = –9
2x + 6y – 5 = 0
→ a2 = 2, b2 = 6, c2 = –5
Now compare the ratios:
Clearly,
⇒ The pair of lines intersect at a unique point.
Q6. The pair of equations x = 4 and x = –1 has:
(a) one solution
(b) two solutions
(c) infinitely many solutions
(d) no solution
Ans: (d)
Given equations:
x = 4 and x = –1
These are two vertical lines on the graph — both are parallel and will never intersect.
Hence, the pair of equations has no solution.
Q7. The value of k for which the pair of linear equations 2x + 3y – 5 = 0 and 4x + ky – 7 = 0 has no solution is:
(a) 3
(b) 5
(c) 6
(d) 3/2
Ans: (c)
We are given:
Equation 1: 2x + 3y – 5 = 0 → a1 = 2, b1=3, c1 =–5
Equation 2: 4x + ky – 7 = 0 → a2 = 4, b2= k, c2 =–7
For the system to have no solution, the condition is:
Step 1:
Step 2:
So the condition for no solution is satisfied when k = 6.
Solving Pair of Linear Equations Algebraically
Q8. If 3x + y = 19 and 5x – y = 21, find the value of x−y.
Sol: Given:
Equation (i): 3x + y = 19
Equation (ii): 5x – y = 21
Add equations (i) and (ii):
(3x+y)+(5x–y)=19+21
⇒8x=40 ⇒x=5
Now substitute x=5 into equation (i):
3×5+y=19
⇒15+y=19
⇒y=4
Now calculate: x–y=5–4=1
Q9. Solve the following pair of linear equations for x and y algebraically:
x + 3y = 10 and y – 2x = 1
Sol: Given equations:
1. x + 3y = 10 ...(i)
2. y – 2x = 1
→ Rewrite as: –2x + y = 1 ..(ii)
Multiply equation (i) by 2:
2(x+3y)=2×10⇒2x+6y=20...(iii)
Now add equation (ii) and (iii):
(–2x+y)+(2x+6y)=1+20⇒7y=21⇒y=3
Now substitute y=3 into equation (i):
x+3(3)=10⇒x+9=10⇒x=1
Q10. Solve the following system of linear equations and verify your answer:
6x − y = 7 and 5x + 3y = 14
Sol: Given equations:
1. 6x − y = 7 ...(i)
2. 5x + 3y = 14 ...(ii)
Let’s eliminate y. Multiply equation (i) by 3:
3(6x−y)=3×7⇒18x−3y=21...(iii)
Now add equations (ii) and (iii):
(5x + 3y) + (18x − 3y) = 14 + 21 ⇒ 23x = 35 ⇒ x = 35/23
Now substitute x= 35/23 into equation (i):
Q11. If the pair of linear equations x – 2y = 0 and kx + y = 7 has a unique solution x = 3, y = 1, then the value of k is:
(a) 1
(b) 2
(c) −1
(d) 4/3
Ans: (b)
Substitute x = 3, y = 1 into the second equation:
kx+y=7
⇒k(3)+1=7
⇒3k=6
⇒k=2
Q12. (A) If we add 2 to the numerator and subtract 2 from the denominator, a fraction becomes 2. It becomes 1/3 if we only add 2 to the denominator. What is the fraction?
OR
(B) For which value of k will the following pair of linear equations have no solution?
4x + y = 2
(3k−1)x+(k−3)y=3k+5
Sol: (A) Let the required fraction be x/y.
First condition:
Second condition:
Substitute equation (i) into equation (ii):
3(2y−6)=y+2
6y−18=y+2
6y−y=20
5y=20
y=4
Substitute y = 4 into equation (i):
x=2(4)−6
x=8−6
x=2
Thus, the required fraction is
x/y = 2/4 = 1/2.
(B) The given equations are:
1. 4x+y=2
2. (3k−1)x+(k−3)y=3k+5
For no solution, the ratios of the coefficients must satisfy the condition:
First, solve for k using the first part:
Cross-multiply:
4(k−3)=3k−1
4k−12=3k−1
4k−3k=12−1
k=11
Now, for the second condition
Cross-multiply:
Thus, for no solution, k=11 and k ≠ - 11
Q13. If 15x−18y=45 and 18x−15y=47, then the value of (x+y) is:
(a) 2
(b) -2
(c) 4
(d) -4
Ans:
Given: 15x−18y=45...(i)
and
18x−15y=47...(ii)
Multiplying (i) by 18 and (ii) by 15, and subtracting, we get:
270x−324y−(270x−225y)=810−705
−99y=105
Now, substitute y = -15/14 into equation (i):
Multiply through by 14 to eliminate the fraction:
Thus, x + y = 12/7 - 15/14.
Simplifying the right-hand side:
Thus, the value of x + y is 9/14.
Graphical Representation and Solutions
Q14. In the given figure, graphs of two linear equations are shown. The pair of these linear equations is: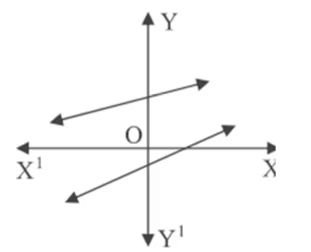
(a) consistent with unique solutions.
(b) consistent with infinitely many solutions.
(c) inconsistent.
(d) inconsistent but can be made consistent by extending these lines.
Ans: (a)
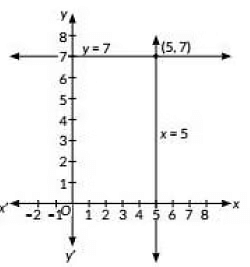
Q15. Solve the pair of equations x = 5 and y = 7 graphically.
Sol: Given equations are
x = 5 ---------------(i)
y = 7 ---------------(ii)
Draw the line x = 5 parallel to the y-axis and y= 7 parallel to the x-axis.
∴ The graph of equation (i) and (ii) is as followsThe lines x = 5 and y = 7 intersect each other at (5, 7).
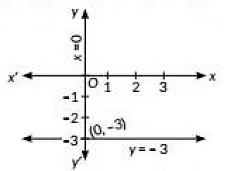
Q16. Using the graphical method, find whether a pair of equations x = 0 and y = -3 is consistent or not.
Sol: Given pair of equations are
x = 0 ------(i)
and y = -3 ------(ii)
x = 0 means y-axis and draw a line y = -3 parallel to x-axis. The graph of given equations (i) and (ii) isThe lines intersect each other at (0, -3). Therefore, the given pair of equations Is consistent.
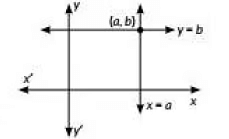
Q17. The pair of equations x = a and y = b graphically represent lines which are
(a) Intersecting at (a, b)
(b) Intersecting at (b, a)
(c) Coincident
(d) Parallel
Ans: (a)
Sol: The pair of equations x = a and y = b graphically represent lines which are parallel to the y-axis and x-axis respectively.
The lines will intersect each other at (a, b).
Applications in Real-World Problems
Q18. Three years ago, Rita was five times as old as Anjali. Ten years later, Rita will be three times as old as Anjali. How old are Rita and Anjali now?
Sol: Let the age of Rita = x years and the age of Anjali = y years
Three years ago:
Rita's age = (x−3) years
Anjali's age = (y−3) years
According to the question,
(x−3)=5(y−3)
x−3=5y−15
x=5y−12...(i)
Ten years later:
Rita's age = x+10
Anjali's age = y+10
According to the question,
(x+10)=3(y+10)
x+10=3y+30
x=3y+20...(ii)
Now, from equations (i) and (ii):
5y−12=3y+20
5y−3y=20+12
2y=32
y=16
Substitute the value of y=16 in equation (i):
x=5×16−12
=80−12
=68
Thus, Rita is 68 years old and Anjali is 16 years old.
Q19. A father is four times as old as his son. In 10 years, he will be three times as old as his son. The sum of the present ages of the father and the son is:
(a) 50 years
(b) 60 years
(c) 70 years
(d) 100 years
Ans: (d)
Let the age of the father be x years and the age of the son be y years.
According to the question,
x=4y...(i)
and
x+10=3(y+10)...(ii)
From equation (ii):
x+10=3y+30
x=3y+20...(iii)
Now, substitute x = 4y from equation (i) into equation (iii):
4y=3y+20
4y−3y=20
y=20
Substitute y=20 into equation (i):
x=4×20=80
Thus, the father is 80 years old, and the son is 20 years old.
The sum of their present ages is:
x+y = 80+20=100 years
Q20. The present age of a father is four years more than twice the age of his son. Four years hence, the father's age will be 12 years more than three times the age of the son. Determine their present ages.
Sol: Let the present age of the son be x years and that of the father be y years.
According to the question, we have:
y=2x+4(i)
and
y+4=3(x+4)+12(ii)
From equation (ii):
y+4=3x+12+12
y+4=3x+24
y=3x+20 (iii)
Now, substitute y=2x+4 from equation (i) into equation (iii):
2x+4=3x+20
2x−3x=20−4
−x=16
x=−16
Q21. A fraction becomes 1/2 when 2 is subtracted from the numerator, and it becomes 1/3 when 6 is added to its denominator. Find the fraction.
Sol: Let the required fraction be x/y.
According to the question, we have:
and
From equation (i):
2(x−2)=y
2x−4=y(iii)
From equation (ii):
3x=y+6
3x−y−6=0(iv)
Now, substitute equation (iii) into equation (iv):
3x−(2x−4)−6=0
3x−2x+4−6=0
x−2=0
x=2
Substituting x = 2 into equation (iii):
2(2)−4=y
4−4=y
y=0
Q22. A fraction becomes 1/4 when 3 is subtracted from the numerator and becomes 1/3 when 2 is subtracted from the denominator. Find the fraction.
Sol: Let the fraction be x/y.
According to the question:
and
From equation (i):
4(x−3)=y
4x−12=y(iii)
From equation (ii):
3x=y−2
3x−y+2=0(iv)
Now, substitute equation (iii) into equation (iv):
3x−(4x−12)+2=0
3x−4x+12+2=0
−x+14=0
x=14
Substituting x=14 into equation (iii):
4(14)−12=y
56−12=y
y=44
Thus, the required fraction is 14/44, which simplifies to 7/22.
Q23. The sum of the numerator and the denominator of a fraction is 20. If the denominator is increased by 3, the fraction reduces to 1/4. Find the fraction.
Sol: Let the numerator be x and the denominator be y of the fraction. Then, the fraction is x/y.
Given,
x+y=20 (i)
and
From equation (ii):
4x = y + 3 (iii)
Now, adding equation (i) and equation (iii):
x+y+4x=20+y+3
5x=23
Substituting x = 23/5 into equation (i):
Thus, the fraction is
Q24. Two schools 'P' and 'Q' decided to award prizes to their students for two games: Hockey Rs. x per student and Cricket Rs. y per student. School 'P' decided to award a total of Rs. 9,500 for the two games to 5 and 4 students, respectively, while school 'Q' decided to award Rs. 7,370 for the two games to 4 and 3 students, respectively.
Based on the given information, answer the following questions:
(i) Represent the following information algebraically (in terms of x and y).
(ii) (a) What is the prize amount for hockey? OR (b) Prize amount on which game is more and by how much?
(iii) What will be the total prize amount if there are 2 students each from the two games?
Sol: (i) Let the prize amount for Hockey per student be x.
Let the prize amount for Cricket per student be y.
From the information provided:
For school 'P': 5x+4y=9500(1)
For school 'Q':
4x+3y=7370(2)
(ii) (a) To find the prize amount for hockey, we will solve the system of equations.
Multiplying equation (1) by 3 and equation (2) by 4, we get:
15x+12y=28500 (3)
16x+12y=29480 (4)
Now, subtract equation (3) from equation (4):
(15x+12y)−(16x+12y)=28500−29480
−x=−980
x=980
Thus, the prize amount for Hockey is Rs. 980 per student.
(b) To find the prize amount for cricket, we will subtract equation (2) from equation (1), but this time, we multiply equation (1) by 4 and equation (2) by 5:
20x+16y=38000 (5)
20x+15y=36850 (6)
Now, subtract equation (6) from equation (5):
(20x+16y)−(20x+15y)=38000−36850
y=1150
Thus, the prize amount for Cricket is Rs. 1150 per student.
Since the prize amount for Cricket is more than Hockey, the difference is:
1150−980=170
Thus, the prize amount for Cricket is more by Rs. 170.
(iii) If there are 2 students each from the two games, the total prize amount will be:
2×980+2×1150=1960+2300=4260
Thus, the total prize amount is Rs. 4260.
Q25. A bookstore shopkeeper gives books on rent for reading. He has a variety of books in his store related to fiction, stories, quizzes, etc. He takes a fixed charge for the first two days and an additional charge for subsequent days. Amruta paid ₹22 for a book and kept it for 6 days, while Radhika paid ₹16 for keeping the book for 4 days.
Assume that the fixed charge is ₹x and the additional charge (per day) is ₹y.
Based on the above information, answer any four of the following questions:
(i) The situation of the amount paid by Radhika is algebraically represented by:
(a) x−4y=16
(b) x+4y=16
(c) x−2y=16
(d) x+2y=16
Ans: (d)
For Amruta, the charges can be represented as:
x+(6−2)y=22
x+4y=22 (i)
For Radhika, the charges can be represented as:
x+(4−2)y=16
x+2y=16(ii)
Thus, the algebraic equation for Radhika's situation is x + 2y = 16, which corresponds to option (d).
Q26. A train covered a certain distance at a uniform speed. If the train had been 6 km/h faster, it would have taken 4 hours less than the scheduled time, and if the train were slower by 6 km/h, it would have taken 6 hours more than the scheduled time. Find the length of the journey.
Sol: Let the original uniform speed of the train be x km/h, and the total length of the journey be l km.
The scheduled time taken by the train to cover a distance of l km is i/x hours.
First condition:
If the speed is increased by 6 km/h, the time taken would be 4 hours less.
Thus, the new time taken at (x+6) km/h ishours, and the equation becomes:
Multiplying both sides by x(x+6) to eliminate the denominators:
Second condition: If the speed is decreased by 6 km/h, the time taken would be 6 hours more.
Thus, the new time taken at (x−6) km/h ishours, and the equation becomes:
Multiplying both sides by x(x−6) to eliminate the denominators:
Equating equations (i) and (ii):
Multiplying both sides by 3:
2x(x+6)=3x(x−6)
Expanding both sides:
2x2+12x=3x2−18x
Rearranging the terms:
2x2+12x−3x2+18x=0
−x2+30x=0
x(x−30)=0
Thus, x=30 (since speed cannot be 0).
Finding the length of the journey:
Substitute x=30 into equation (ii): l = 30(30 − 6) = 30 × 24 = 720
|
127 videos|584 docs|79 tests
|
FAQs on Important Questions: Pair of Linear Equations in Two Variables - Mathematics (Maths) Class 10
| 1. What are the conditions for a pair of linear equations to have a unique solution? |  |
| 2. How do you determine if a pair of linear equations has no solution? |  |
| 3. What does it mean for a pair of linear equations to have infinitely many solutions? |  |
| 4. How can you graphically represent the solutions of a pair of linear equations? |  |
| 5. What methods can be used to solve a pair of linear equations? |  |