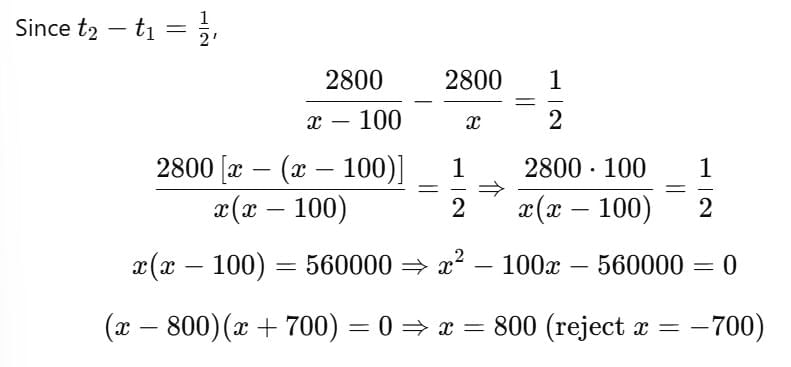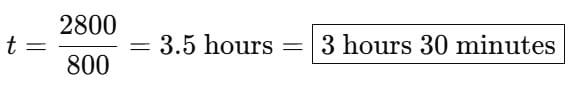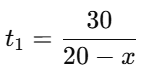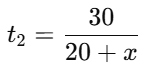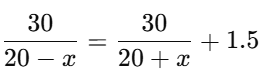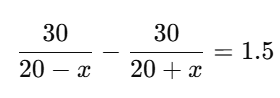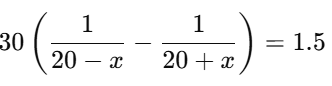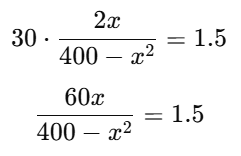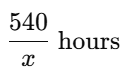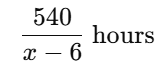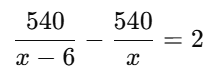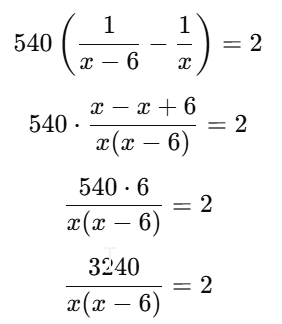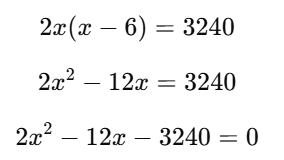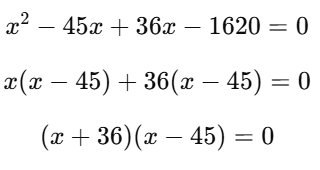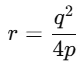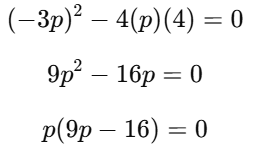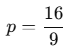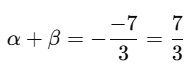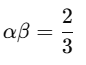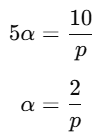Important Questions: Quadratic Equations | Mathematics (Maths) Class 10 PDF Download
Formation and Solution of Quadratic Equations
Q1. In a flight of 2800 km, an aircraft was slowed down due to technical issues. Its average speed decreased by 100 km/h, which caused the flight time to increase by 30 minutes. Find the original duration of the flight.
Ans:
Distance = 2800 km
Original speed = x km/h
Reduced speed = x−100 km/h
Increase in time = 30 minutes =1/2 hourLet original time t1=
hrs,
time at reduced speed t2 =
hrs
Original Duration:
Q2. The denominator of a fraction is 1 more than twice the numerator. If the sum of the fraction and its reciprocal is 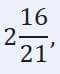 , find the fraction.
, find the fraction.
Ans: Let the numerator of the required fraction be x.
Then, its denominator = (2x + 1).
∴ fraction = x/(2x + 1) and its reciprocal = (2x + 1)/x.
∴ x/(2x + 1) + (2x + 1)/x = 58/21
⇒ 21 × [x² + (2x + 1)²] = 58x(2x + 1)
⇒ 21 × [5x² + 4x + 1] = 116x² + 58x
⇒ 11x² - 26x - 21 = 0
⇒ 11x² - 33x + 7x - 21 = 0 ⇒ 11x(x - 3) + 7(x - 3) = 0
⇒ (x - 3)(11x + 7) = 0 ⇒ x - 3 = 0 or 11x + 7 = 0
⇒ x = 3 or x = -7/11
⇒ x = 3 [∵ numerator cannot be a negative fraction].
∴ required fraction = x/(2x + 1) = 3/7.
Q3. A rectangular floor area can be completely tiled using 200 square tiles. If the side length of each tile is increased by 1 unit, it would take only 128 tiles to cover the floor.
(i) Assuming the original length of each side of a tile is x units, form a quadratic equation from the above information.
(ii) Write the corresponding quadratic equation in standard form.
(iii)
(a) Find the value of x, the side of the tile, by factorisation.
OR
(b) Solve the quadratic equation using the quadratic formula.
Ans:
i. Let the original side length of each tile be x units.
The area of the rectangular floor using 200 tiles = 200 x2 unit2
The area with increased side length (each side increased by 1 unit) using 128 tiles = 128 (x + 1)2 unit2
So, the required quadratic equation is: 200x2 = 128 (x + 1)2
ii. We have,
200x2 = 128 (x + 1)2
⇒ 200x2 = 128 (x2 + 2x + 1)
⇒ 200x2 = 128x2 + 256x + 128
⇒ 72x2 − 256x − 128 = 0
which is the quadratic equation is standard form.iii.
a. We have, 72x2 − 256x − 128 = 0
or, 9x2 − 32x − 16 = 0
or, 9x2 − 36x + 4x − 16 = 0
or, 9x (x − 4) + 4 (x − 4) = 0
or, (x − 4) (9x + 4) = 0
or, x = 4, −4/9
Since the side cannot be negative, thus x = 4 units.OR
b. We have 9x2 − 32x − 16 = 0
On comparing with ax2 + bx + c = 0, we get a = 9, b = −32, c = −16Using quadratic formula,
x = [−(−32) ± √((−32)2 − 4 × 9 × (−16))] / (2 × 9)
= [32 ± √(1024 + 576)] / 18
= [32 ± √1600] / 18
= [32 ± 40] / 18
= (32 + 40)/18 or (32 − 40)/18
= 72/18 or −8/18 = 4 or −4/9
Q4. The sum of two numbers is 20. If 2 is subtracted from one number and 1 is added to the other, the product of these two new numbers becomes 96. Find the numbers.
Ans: Let one number be x, then the other number will be:
y = 20 - x → (1)
According to the question:
(x - 2)(y + 1) = 96 → (2)
Now substitute the value of y from (1) into (2):
(x - 2) × ((20 - x) + 1) = 96
⇒ (x - 2)(21 - x) = 96Now expand the expression:
= 21x - x² - 42 + 2x
= -x² + 23x - 42So,
-x² + 23x - 42 = 96
Bring all terms to one side:
-x² + 23x - 138 = 0
Multiply through by -1:x² - 23x + 138 = 0
Now factor the quadratic:
x² - 23x + 138 = 0
⇒ (x - 6)(x - 23) = 0So, x = 6 or x = 23
From equation (1), y = 20 - x:
If x = 6, then y = 14
If x = 23, then y = -3We discard the negative value, since we want two positive numbers.
Speed, Distance, and Time Problems
Q5. A motorboat whose speed in still water is 20 km/h takes 1.5 hours more to go 30 km upstream than to return downstream to the same location. Find the speed of the stream.
Ans: Speed of boat in still water = 20 km/h
Distance = 30 km
Let the speed of the stream be x km/h
Then:
- Upstream speed = 20−x km/h
- Downstream speed = 20+x km/h
Time taken upstream:
Time taken downstream:
According to the question:
t1 = t2 + 1.5
Substitute the values:Now simplify:
Take LHS:
Now use identity:
So:
Multiply both sides by (400−x2):
60x = 1.5(400 − x2)
60x = 600 − 1.5x2
Bring all terms to one side:
1.5x2+60x−600=0
Multiply through by 2 to remove decimal:
3x2+120x−1200=0
Divide by 3 to simplify:
x2+40x−400=0
Now factorise:
Split middle term: x2 + 50x − 10x − 400 = 0
x(x+50)−10(x+50)=0
(x+50)(x−10)=0
So, x=−50 or x=10
The speed of the stream is 10 km/h
Q6. A train covers a distance of 540 km at a uniform speed. If the speed had been 6 km/h less, it would have taken 2 hours more to cover the same distance. Find the original speed of the train.
Ans: Let the original speed of the train be x km/h.
Then, time taken to cover 540 km at speed x =
If the speed is reduced by 6 km/h, then new speed = x−6 km/h New time taken =
According to the question:
Take LHS:
Cross-multiply:
Divide entire equation by 2: x2−6x−1620=0
Now factorise:
Try splitting the middle term:
So, x=−36 or x=45
Reject negative speed.
The original speed of the train is 45 km/h
Roots of Quadratic Equations
Q7. If the roots of the quadratic equation 9x2 − 12x + m = 0 are real and equal, then the value of m is:
(a) 16/9
(b) 4/3
(c) 144/81
(d) 36/25
(e) 4
Ans: (e)
Given: Quadratic equation: 9x2 − 12x + m = 0
Compare with standard form ax2 + bx + c = 0, we get:
- a = 9
- b = −12
- c = m
For real and equal roots, the discriminant D = 0:
D = b2 − 4ac = 0
(−12)2−4(9)(m)=0⇒144−36m=0⇒36m=144⇒ m = 144/36 = 4
Q8. If the roots of the quadratic equation px2 + qx + r = 0,where p ≠= 0, are real and equal, then which of the following relations must be true?
(a) 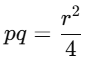
(b) 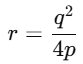
(c) q2 = 2pr
(d) 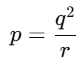
Ans: (b)
For real and equal roots, the discriminant must be zero:
D = q2 − 4pr = 0 ⇒ q2 = 4pr ⇒ r =
Q9. Find the discriminant of the quadratic equation 3x2 + 7x − 4 = 0 and comment on the nature of the roots.
Ans: Given quadratic equation: 3x2 + 7x − 4 = 0
For a quadratic equation ax2 + bx + c = 0, the discriminant D is given by: D = b2 − 4ac
Here, a = 3, b = 7, and c = −4.
Substitute these values into the discriminant formula:
D = 72 − 4(3)(−4) = 49 + 48 = 97
Since D>0, the roots of the quadratic equation are real and distinct.
Q10. Find the value of p for which the quadratic equation p⋅x(x − 3) + 4 = 0 has two equal real roots.
Ans: The given quadratic equation is: p⋅x(x−3)+4=0
Expanding this:
p⋅x2−3px+4=0
Comparing with the standard quadratic equation ax2 + bx + c = 0, we have:
- a=p
- b=−3p
- c=4
For the equation to have two equal real roots, the discriminant must be zero:
D=b2−4ac=0
Substitute the values of a, b, and c:
Thus, p=0 or p= 16/9
Since p ≠= 0 (as it would make the equation linear), we conclude that the value of p is:
Q11. Find the sum and product of the roots of the quadratic equation 3x2 − 7x + 2 = 0.
Ans: Let the roots of the quadratic equation 3x2 − 7x + 2 = 0 be α and β.
Using the sum and product of roots formulas for a quadratic equation ax2 + bx + c = 0:
- Sum of roots α + β = − b/a
- Product of roots αβ= c/a
For the given equation 3x2 −7x + 2 = 0, we have:
- a = 3
- b = −7
- c = 2
So,
Sum of roots:
Product of roots:
Q12. Find the value of p, for which one root of the quadratic equation px2 − 10x + 5 = 0 is 4 times the other.
Ans: Let the first root be α, and the second root will be 4α.
Sum of roots is given by:
For the equation px2 −10x + 5 = 0, we have:
- a = p
- b = −10
Thus, the sum of the roots is:
Product of roots is given by:
For the equation px2 − 10x + 5 = 0, we have:
c = 5
Thus, the product of the roots is:
Substitute α = 2/p:
Cross-multiply:
16p = 5p2
5p2 − 16p = 0
Factor the quadratic equation:
p(5p−16)=0
Thus, p = 0 or p= 16/5.
Since p=0 is not valid for a quadratic equation, we conclude:
p=16/5
Q13. The quadratic equation (1 + a2)x2 + 2abx + (b2 − c2) = 0 has only one root. What is the value of c2(1 + a2)?
Ans: Given quadratic equation:
(1 + a2)x2 + 2abx + (b2 − c2) = 0
Comparing it with the standard form Ax2 + Bx + C = 0, we identify the following coefficients:
- A=1+a2
- B=2ab
- C = b2 − c2
For the quadratic equation to have only one root, the discriminant must be zero. The discriminant Δ is given by:
Δ = B2 − 4AC
Substitute the values of A, B, and C:
Δ = (2ab)2 − 4 × (1 + a2) × (b2 − c2)
Simplifying:
Δ = 4a2b2−4(1+a2)(b2−c2)
Expanding:
Δ = 4a2b2−4(b2−c2+a2b2−a2c2)
Simplifying further:
Δ = 4a2b2−4b2+4c2−4a2b2+4a2c2
Now, cancel out the 4a2 b2 terms:
Δ = −4b2 + 4c2 + 4a2c2
For the discriminant to be zero:
−4b2+4c2+4a2c2=0
Divide through by 4:
−b2+c2+a2c2=0
Rearranging:
c2+a2c2=b2
Factor out c2:
c2(1+a2)=b2
Thus, the value of c2 (1+a2) is: b2
|
127 videos|584 docs|79 tests
|
FAQs on Important Questions: Quadratic Equations - Mathematics (Maths) Class 10
| 1. What are the different methods to solve quadratic equations? |  |
| 2. What is the significance of the discriminant in a quadratic equation? |  |
| 3. Can a quadratic equation have more than two roots? |  |
| 4. How can one derive the quadratic formula? |  |
| 5. What is the vertex form of a quadratic equation, and how is it useful? |  |