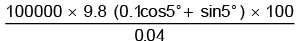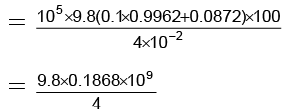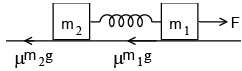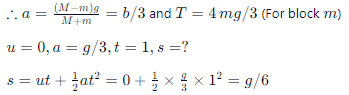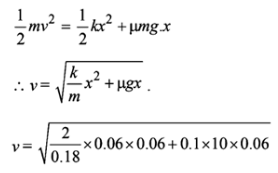Integer Answer Type Questions for JEE: Work, Power & Energy | Chapter-wise Tests for JEE Main & Advanced PDF Download
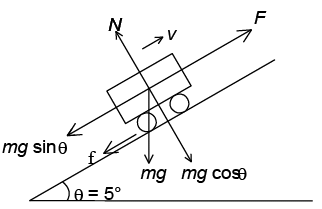
Q.1. A 100000 kg engine is moving up a slope of gradient 5° at a speed of 100 m/hr. The coefficient of friction between the engine and the rails is 0.1. If the engine has an efficiency of 4% for converting heat into work, find the amount of coal, the engine has to burn up in one hour. (Burning of 1 kg of coal yields 50000 J.)
Ans. 9154 kg
The forces are shown in Figure.Net force to move the engine up the slope.
F = μN + mg sin θ
= mg (μ cos θ + sin θ)
If the engine has to apply an upward force equal to F,
power of engine, P = Fv
where v is the velocity equal to 100 m/hr.Work done by engine, W = Pt = Fvt
Efficiency of engine, η = output/Input = Fvt/Energy used
= Energy used by engine = Fvt/η = mg(mcosq+sinq)vt/η
m = 100000 kg, μ = 0.1, θ = 5°, v = 100 m/hr, t = 1 hr
η = 4/100 = 0.04Energy used by engine =
= 4.577 x 108 JAs 1 kg coal yields 50000 J, we have the amount of coal burnt up
== 9154 kg
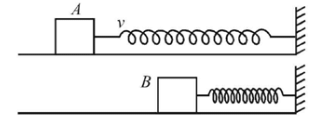
Q.2. Two bars of masses m1 = 4 kg and m2 = 8kg connected by a non-deformed light spring rest on a horizontal plane. The coefficient of friction between bars and surface is μ = 0.2. What minimum constant force has to be applied in the horizontal direction to the bar of mass m1 in order to shift the other bar?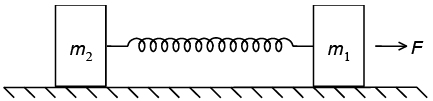
Ans. 16 N
Let F be the force applied as shown in the Figure. If F moves through x, the work done will be F x x.
This is used to work against friction μm1g and store energy in the spring.
Work done against friction = μm1gx;
Energy stored = 1/2kx2 , where k is the spring constant.
∴ F × x = μm1gx + 1/2kx2... (i)
When the mass m2moves, the tension in the spring balances the force of friction at m2.
∴ kx = μm2g ... (ii)
∴ combining equations (i) and (ii),
F × x = μm1gx +1/2μm2g × x
F == 16 N
Q.3. Two masses 10 kg and 20 kg are connected by a massless spring. A force of 200 N acts on 20 kg mass. At the instant when the 10 kg mass has an acceleration 12 m/s2 the energy stored in the spring (k = 2400 N/m) will be
Ans. 3 J
F = 10 x 12 = 120 N
F = kx = 2400 x
∴ x = 1/20
Energy stored in the spring E = 1/2 kx2= 3 J
Q.4. A body is projected at an angle of 30° to the horizontal with kinetic energy 40 J. What will be the kinetic energy at the top most point?
Ans. 30 J
At the topmost point, the horizontal component of velocity = u cos α
∴ Initial kinetic energy = 1/2 mu2 = 40 J
Kinetic energy at the topmost point = 1/2 mu2 cos 2 α
= 40 cos2α
= 40x3/4 = 30 J
Q.5. A body is slowly lowered on to a massive platform moving horizontally at a speed of 4 m/s. through what distance will the body slide relative to the platform? (The coefficient of friction is 0.2; g = 10 m/s2)
Ans. 4 m
The frictional force between the body and the platform = μmg, where m is the mass of the body.
Initially the relative velocity = 4 m/s
The relative retardation = μg= 0.2 x 10
= 2 m/s2
If S is the relative displacement before the relative velocity becomes zero, we have
0 = 42 – 2 x 2 x SS = 16/4 = 4 m
Q.6. A ball falls under gravity from a height 10 m with an initial velocity v0. It hits the ground, loses 50% of its energy in collision and it rises to the same height. What is the value of v0?
Ans. 14 m/s
Let v be the velocity when it hits the ground.
Then v2 –
= 2g x 10 = 2 x 9.8 x 10
i.e., v2 =+ 196
Let v' be the velocity after impact and it reaches the same height 10 m.
v'2 - 0 = 2 x 9.8 x 10
v'2 = 196
v' = 14 m/s
Ratio of kinetic energy before impact and after impact
∴= 2 x 196 – 196 = 196
v0 = 14 m/s.
Q.7. A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses 0.36 kg and 0.72 kg. Taking g = 10 m/s2, find the work done (in joules) by the string on the block of mass 0.36 kg during the first second after the system is released from rest.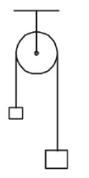
Ans. 8 J
Given m = 0.36kg, M = 0.72kg.
The figure shows the forces on m and M.
When the system is released, let the acceleration be a. Then
Given m = 0.36kg, M = 0.72kg.
The figure shows the forces on m and M.
When the system is released, let the acceleration be a. Then
T = mg = maMg − T = M
∴ Work done by the string on m is
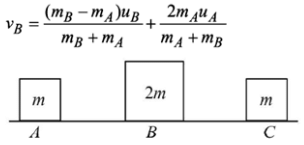
Q.8. Three objects A, B and C are kept in a straight line on a frictionless horizontal surface. These have masses m, 2m and m, respectively. The object A moves towards B with a speed 9 m/s and makes an elastic collision with it. There after, B makes completely inelastic collision with C. All motions occur on the same straight line. Find the final speed (in m/s) of the object C.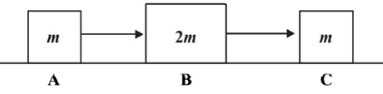
Ans. 4m/s
The velocity of B just after collision with A is
The collision between B and C is completely inelastic.
∴ mB vB = (mB +mc)v
Q.9. A block of mass 0.18 kg is attached to a spring of force-constant 2 N/m. The coefficient of friction between the block and the floor is 0.1. Initially the block is at rest and the spring is un stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06 m and comes to rest for the first time. The initial velocity of the block in m/s is V = N/10. Then N is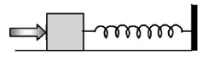
Ans. 4
Let v be the speed of the block just after impulse. At B, the block comes to rest. Therefore
Loss in K.E. of the block = Gain in RE. of the spring + Work done against friction
∴ v = 4/10 ∴ N = 4
Q.10. A particle of mass 0.2 kg is moving in one dimension under a force that delivers a constant power 0.5 W to the particle. If the initial speed (in ms-1) of the particle is zero, the speed (in ms-1) after 5 s is
Ans. 5ms-1
Here Δ K.E. = W = p x t
∴ 1/2 mv2 = P x t
|
481 docs|964 tests
|