Integrated Rate Equations: Zero, First & Second Order Reactions | Chemistry Class 12 - NEET PDF Download
What are Integrated Rate Equations?
Integrated rate equations are mathematical expressions that relate the concentrations of reactants and/or products to time for a chemical reaction.
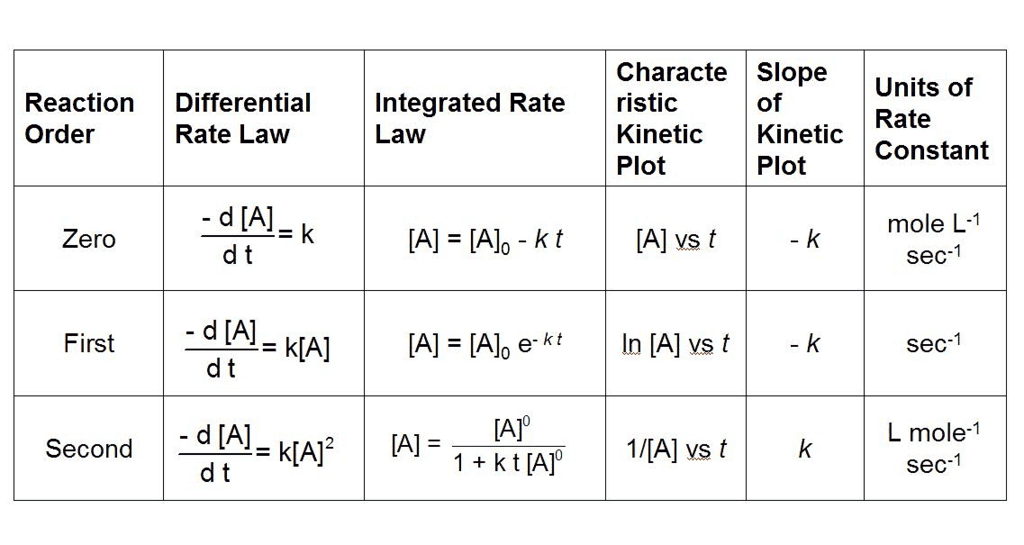
These equations are obtained by integrating the rate laws, which describe how the rate of a reaction depends on the concentrations of reactants.
- The integrated rate equations provide a way to directly relate concentration and time, allowing for the determination of reaction kinetics and the calculation of reaction constants.
- The form of the integrated rate equation depends on the order of the reaction, which is determined experimentally.
- The three most common types of reaction orders are zero order, first order, and second order. Here are the integrated rate equations for each:
(i) Zero Order Reactions
The rate law for zero order reactions (n = 0) is written as :
-
-
[A]o - [A] = kt
=
Half-life (t 1/2) of Zero Order Reaction
Time in which half of initial amount is left.
[A]o [A]o/2
t = o t = t1/2
k =
t1/2 =
Thus, for a Zero order reaction, half-life is directly proportional to the initial concentration of the reactant.
Clearly, zero-order reactions are those, whose rates are not affected by change in concentrations of reactants (i.e., independent of concentration). The rates of such reactions only depend upon temperature. Most of photochemical reactions are zero order reactions. Other examples are : decomposition of HI over the surface of gold and NH3 over tungsten.
Example :
(1) Photochemical Reactions, Photosynthesis
(2) CH4 Cl2
Cl - Cl Cl
CH4 + Cl CH3Cl + H
(ii) First Order reaction
A product
t = o [A]o -
t = t [A] [P]
ln [A]o/[A] = kt
Half life (t1/2) of First Order Reaction
t = t1/2 [A] = [A]o/2
=
[A] = where , n = number of half lifes.
Average life
Features of a First Order Reaction
1. A first order reaction must follow above form of rate law for all time instants.
This means if we are given value of A0 and values of x at different time instants [i.e.(A0 - x) as value of reactants after t], the values of k can be calculated for different time instants by using the above first order law.
If the reaction for which the data were given is a first order reaction, then all values of k will approximately equal to each other.
2. The time for half reaction for a first order reaction is independent of initial concentration of reactants.
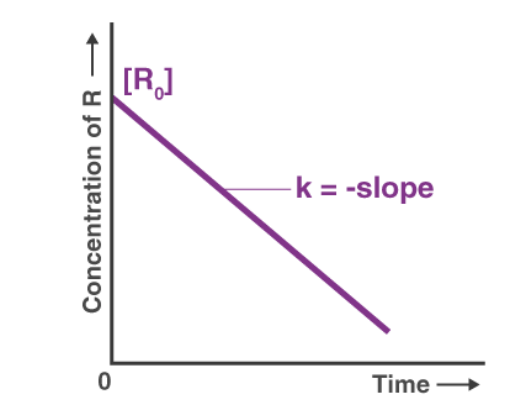
3. The concentration of reactants in a first order reaction decreases exponentially with time (see figure)
Note that plot of log10 A vs t is linear.
Example :
(1) Radioactive disintegration.
(2) PCl5(g) -> PCl3(g) Cl2(g)
(3) H2O2 → H2O + 1/2O2
(4) NH4NO2 → N2 +2H2O
Rate constant of a first order reaction can also be calculated by measuring the concentration of the reactants at two time instants (if the initial concentration is not known).
If A1 and A2 are the reactant's concentrations at two time instants 't1' and 't2' respectively, then we have :
...(iii)
and ... (iv)
Subtracting (iv) from (iii), we get :
Thus, k can be evaluated.
Example: For a reaction 2NO(g) + 2H2(g) → N2(g) + 2H2O (g) ; the following data were obtained.
| [NO] (mol/L) | [H2](mol/L) | Rate (mol/L/s) |
1. | 5 X 10-3 | 2.5 X 10-3 | 3 X 10-5 |
2. | 15 X 10-3 | 2.5 X 10-3 | 9 X 10-5 |
3. | 15 X 10-3 | 10 X 10-3 | 3.6 X 10-4 |
(a) Calculate the order of reaction.
(b) Find the rate constant.
(c) Find the initial rate if [NO] = [H2] = 8.0 x 10-3 M
Solution: Assuming rate law can be expressed as follows :
rate = k[NO]x [H2]y
By analyzing the data :
From observation 1 and 2, we see that [H2] is constant and when [NO] is tripled, the rate is also tripled.
⇒ rate (r) ∝ [NO] ⇒ x = 1
From observations 2 and 3, we see that [NO] is constant; when [H2] is increased four times, the rate also increases four times :
rate ∝ [H2] ⇒ y = 1
⇒ r = k [NO] [H2O]
⇒ The order of reaction w.r.t No and H2 is 1 and the overall order of reaction is 1 1 = 2.
Initial rate = k[NO][H2] = 2.4 x (8 x 10-3)2 = 1.536 x 10-4 mol/L/s.
(iii) Second Order Reaction
Case I :
- = k[A]2
k =
Half-life (t1/2) of Second-Order Reaction
[A]t = , k = 2/[A]o - 1/[A]o
t1/2 =
Example :
- Alkaline hydrolysis of esters.
- Self Cannizzaro's reactions,
Case (II):
- ,
,
ln
k =
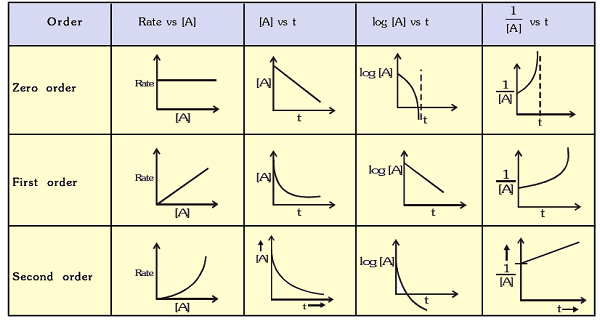
Graphs of Zero, First and second Order Reactions
|
75 videos|278 docs|78 tests
|
FAQs on Integrated Rate Equations: Zero, First & Second Order Reactions - Chemistry Class 12 - NEET
| 1. What is the difference between zero-order, first-order, and second-order reactions? |  |
| 2. How is the half-life of a zero-order reaction related to the initial concentration of the reactant? |  |
| 3. How can you determine the rate constant of a first-order reaction from experimental data? |  |
| 4. What factors can influence the rate of a second-order reaction? |  |
| 5. How do integrated rate equations help in understanding the kinetics of chemical reactions? |  |






















