Electrostatic Potential & Capacitance | Physics Class 12 - NEET PDF Download
Electrostatic Potential
The electrostatic potential is also known as the electric field potential, electric potential, or potential drop is defined as:
The work done in bringing the charge from infinity to the given point in the electric field.

- Electric potential is a scalar property of every point in the region of the electric field. At a point in the electric field, the potential is defined as the interaction energy of a unit positive charge. If at a point in the electric field a charge q0 has potential energy U, then the electric potential at that point can be given as:

- Potential at a point can be physically interpreted as the work done within the conservative field in displacing a unit (+ve) charge from infinity to that point.
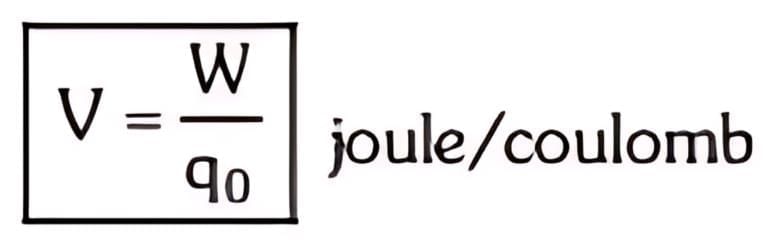
Electric Potential is the ‘push’ of electricity through a circuit. It’s easy to confuse electric potential with electric current, so it helps to think of electric current as the water in our shower and electric potential as the water pressure. Like water pressure, the varying voltage can increase or decrease the flow of electricity.
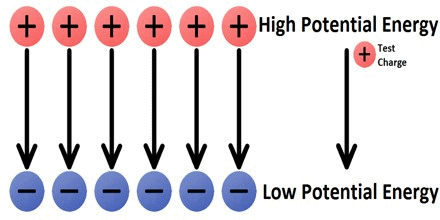 Test charge moves from high potential to low potential
Test charge moves from high potential to low potential
Electric Potential in Circuits
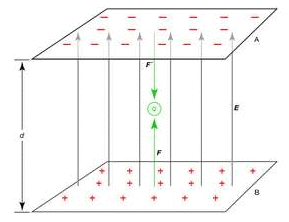
- A charge moving through the wires of the circuit will encounter changes in electric potential as it traverses the circuit. Within the electrochemical cells of the battery, there is an electric field established between the two terminals, directed from the positive terminal towards the negative terminal.
- As such, the movement of a positive test charge through the cells from the negative terminal to the positive terminal would require work, thus increasing the potential energy of every Coulomb of charge that moves along this path.
 Electric potential movement in circuits
Electric potential movement in circuits - This corresponds to a movement of the positive charge against the electric field. It is for this reason that the positive terminal is described as the high potential terminal. The charge would lose potential energy as moves through the external circuit from the positive terminal to the negative terminal.
- The negative terminal is described as the low potential terminal. This assignment of high and low potential to the terminals of an electrochemical cell presumes the traditional convention that electric fields are based on the direction of movement of positive test charges.
- Chemical energy is transformed into electric potential energy within the internal circuit (i.e., the battery). Once at the high potential terminal, a positive test charge will then move through the external circuit and do work upon the light bulb or the motor or the heater coils, transforming its electric potential energy into useful forms for which the circuit was designed.
- The positive test charge returns to the negative terminal at low energy and low potential, ready to repeat the cycle (or should we say circuit) all over again.
Electric Potential Difference
For any charge, an electric potential is obtained by dividing the electric potential energy by the quantity of charge.
In an electrical circuit, the electric potential between two points is defined as the amount of work done by an external agent in moving a unit charge from one point to another.
Mathematically, 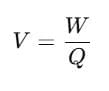
Where,
V = electrical potential difference between two points
W = Work done in moving a charge from one point to another
Q = the quantity of charge in coulombs
The potential difference is measured by an instrument called a voltmeter. The two terminals of a voltmeter are always connected parallel in across the points whose potential is to be measured.
Electrostatic Potential due to a Point Charge
Let P be the point at a distance r from the origin O at which the electric potential due to charge +q is required.
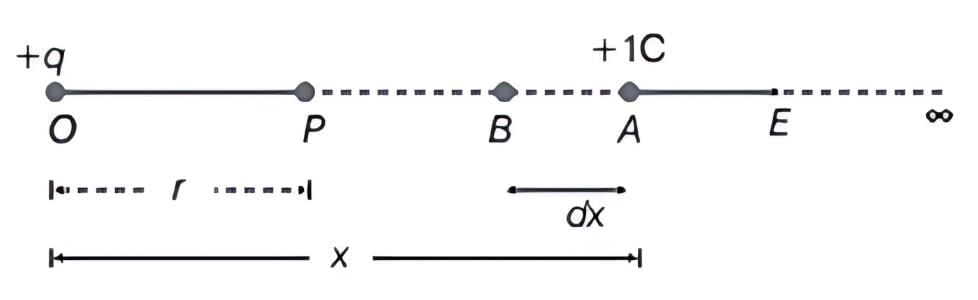
The electric potential at a point P is the amount of work done in carrying a unit positive charge from ∞ to P. As work done is independent of the path, we choose a convenient path along the radial direction from infinity to the point P without acceleration. Let A be an intermediate point on this path where OA = x. The electrostatic force on a unit positive charge at A is given by
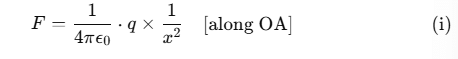
Small work done in moving the charge through a distance dx from A to B is given by
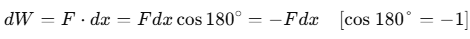
⇒ dW = Fdx (ii)
Total work done in moving a unit positive charge from P is given by
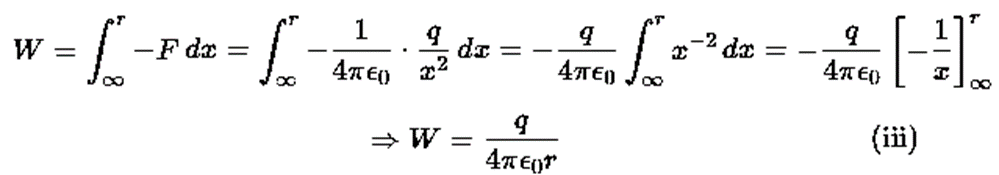
From the definition of electric potential, this work is equal to the potential at point P.

A positively charged particle produces a positive electric potential. A negatively charged particle produces a negative electric potential. Here, we assume that electrostatic potential is zero at infinity. Eq.(iv) shows that at equal distances from a point charge q, value of V is same.
Hence, electrostatic potential due to a single charge is spherically symmetric.
The figure given below shows the variation of electrostatic potential with distance, i.e. and also the variation of electrostatic field with distance, i.e. 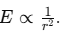
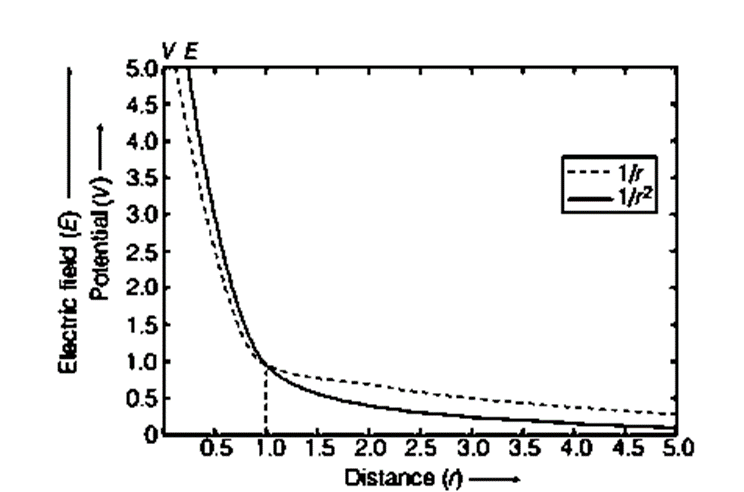 Variation of electrostatic potential V and electric field E with distance r
Variation of electrostatic potential V and electric field E with distance r
Due to a single charge, F ∝ 1/r², E ∝ 1/r² but V ∝ 1/r, where
r is the distance from the charge.
Electrostatic Potential Due to a System of Charges
To find the electric potential at a point P due to multiple point charges 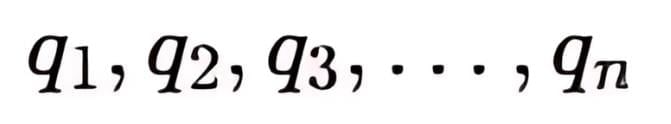 located at respective distances
located at respective distances 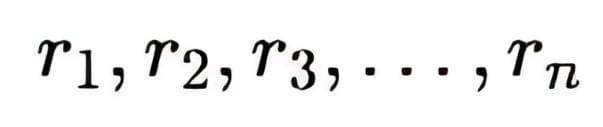 from P, we calculate the potential contribution from each charge and then sum them.
from P, we calculate the potential contribution from each charge and then sum them.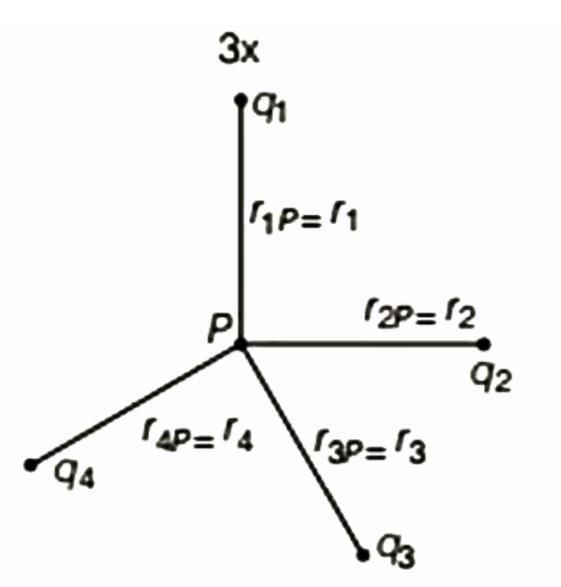 A system of charges
A system of charges
The potential at P due to charge q1 is:
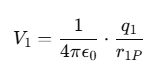
Similarly, the potentials due to other charges are: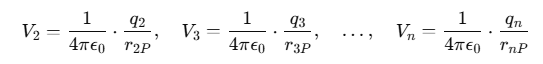
Using the superposition principle, the total potential V at point P is the algebraic sum of the potentials due to each individual charge: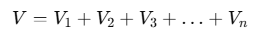
This can be expressed as: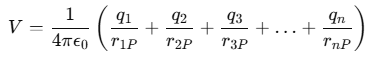
Or, using summation notation:
Thus, the net electrostatic potential Vnet at a point due to multiple charges is the algebraic sum of the potentials from each individual charge at that location: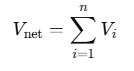
Equipotential Surface
It is that surface where the potential at any point of the surface has the same value.
The electric lines of force and the equipotential surface are mutually perpendicular to each other. No work is done in moving a charge from one point to other on an equipotential surface. Work is done in moving a charge from one equipotential surface to another.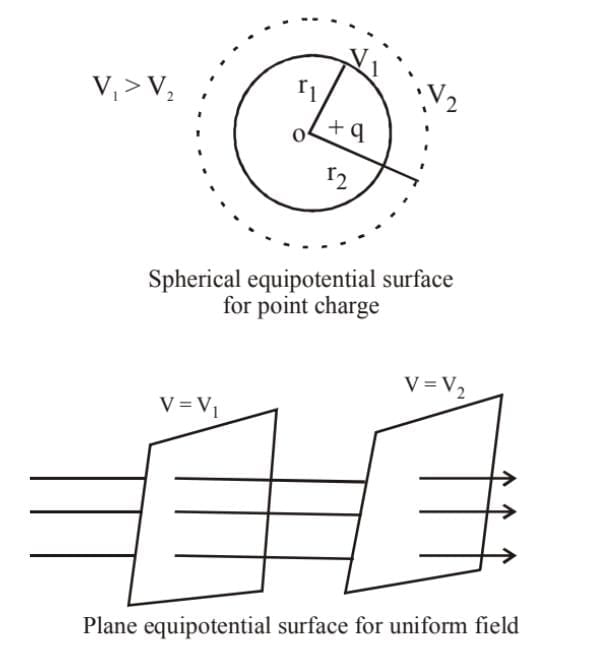
- Equipotential surface do not cut each other.
- The density of the equipotential lines gives an idea of the strength of electric field at that point. Higher the density, larger is the field strength.
Electrostatic Potential due to an Electric Dipole
Let us consider an electric dipole consisting of charges +q and -q separated by a distance 2a. The dipole moment 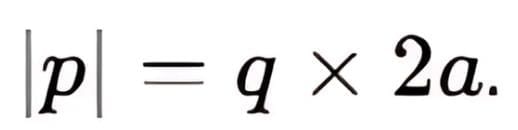
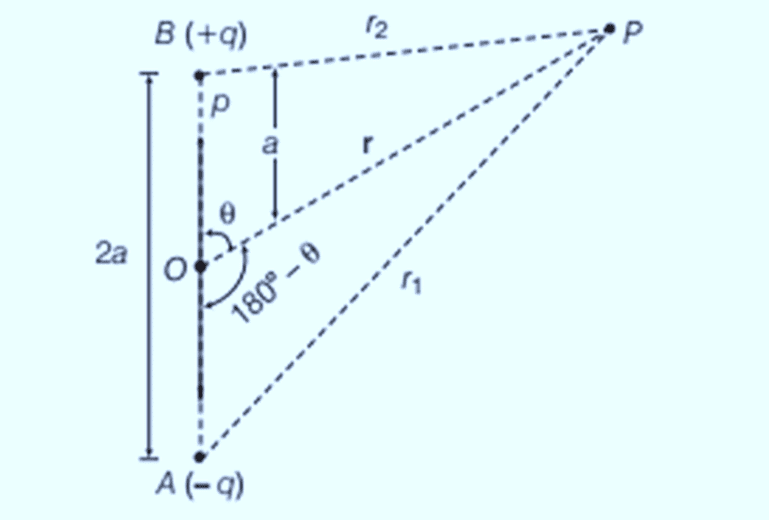 Electric potential at point P due to electric dipoleLet O be the centre of the dipole, P be any point near the electric dipole inclined at an angle θ as shown in the figure. Let P be the point at which electric potential is required.
Electric potential at point P due to electric dipoleLet O be the centre of the dipole, P be any point near the electric dipole inclined at an angle θ as shown in the figure. Let P be the point at which electric potential is required.
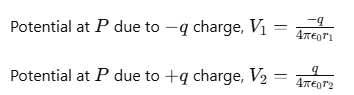
As potential is related to work done by the field, electrostatic potential also follows the superposition principle. Therefore, potential at P due to the dipole,
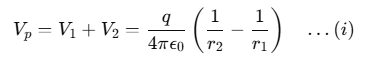
Now, by geometry,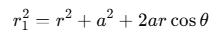
Similarly,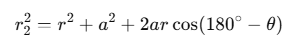
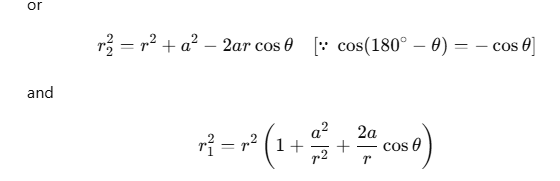
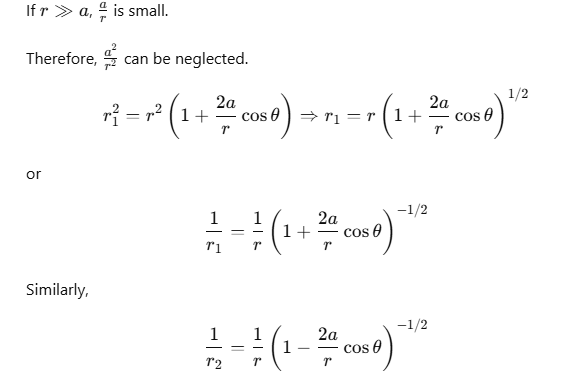
Putting these values in Eq. (i), we obtain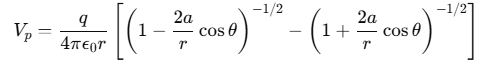
Using Binomial theorem, 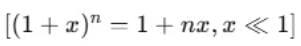 and retaining terms up to the first order in a/r, we get
and retaining terms up to the first order in a/r, we get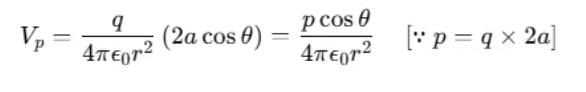
As, 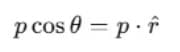 where,
where, 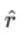 is a unit vector along the position vector OP = r.
is a unit vector along the position vector OP = r.
Therefore, Electrostatic potential at point P due to a short dipole (a << r) is given by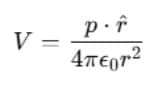 .
.
Example 1. An electric dipole consists of two charges of equal magnitude and opposite signs separated by a distance 2a as shown in figure. The dipole is along the X-axis and is centred at the origin.
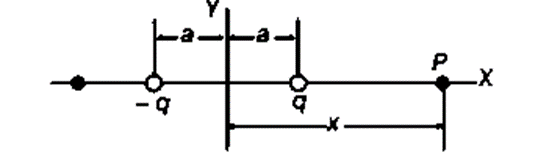
- Calculate the electric potential at point P.
- Calculate V at a point far from the dipole.
Sol. (i) For the point P in figure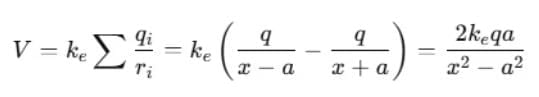
(ii) If point P is far from the dipole, such that x >> a, then a2 can be neglected in the terms, x2 - a2 and V becomes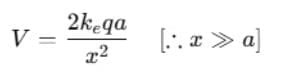
Example 2. Two point charges of 4μC and −2μC are separated by a distance of 1 m in air. Find the location of a point on the line joining the two charges, where the electric potential is zero.
Sol. Let the electrostatic potential be zero at point P between the two charges separated by a distance x meter.
At point P,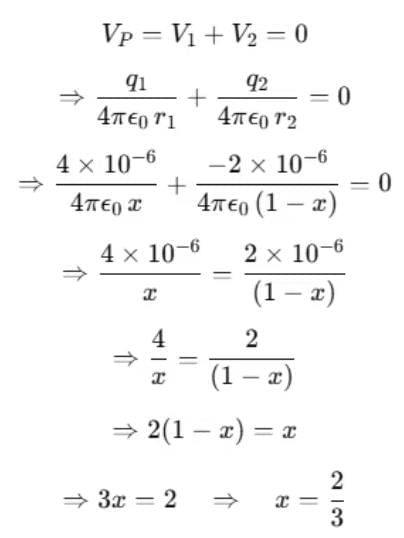
Therefore, the Electrostatic potential is zero at a distance of 2/3 m from charge 4 microcoulomb between the two charges.
Capacitor
Capacitors are also known as Electric condensers. A capacitor is a two-terminal electric component. It has the ability or capacity to store energy in the form of electric charge.
- The capacitor is an arrangement of two conductors generally carrying charges of equal magnitudes and opposite sign and separated by an insulating medium.
- Capacitors vary in shape and size, but the basic configuration is two conductors carrying equal but opposite charges.

What are Capacitors Used For?
Capacitors have many important applications in electronics. Some examples include storing electric potential energy, delaying voltage changes when coupled with resistors, filtering out unwanted frequency signals, forming resonant circuits and making frequency-dependent and independent voltage dividers when combined with resistors.
When charges are pulled apart, energy is associated with the pulling apart of charges, just like energy is involved in stretching a spring. Thus, some energy is stored in capacitors. In the uncharged state, the charge on either one of the conductors in the capacitor is zero.
During the charging process, a charge Q is moved from one conductor to the other one, giving one conductor a charge Q and the other one a charge -Q. A potential difference ΔV is created with the positively charged conductor at a higher potential than the negatively charged conductor.  Applications of Capacitors
Applications of Capacitors
Note:
- The net charge on the capacitor as a whole is zero. When we say that a capacitor has a charge Q, we mean that the positively charged conductor has charge +Q and negatively charged conductor has a charge, -Q.
- In a circuit a capacitor is represented by the symbol:
Capacitance
The capacitance of the conductor is defined as the charge required to increase the potential of a conductor by one unit. It is a scalar quantity.
- Unit of capacitance is farad in SI units and its dimensional formula is [M-1L-2I2T4].
- Capacitance is nothing but the ability of a capacitor to store the energy in form of an electric charge. In other words, capacitance is the storing ability of a capacitor. It is measured in farads.
- 1 Farad: 1 Farad is the capacitance of a conductor for which 1-coulomb charge increases potential by 1 volt.
1 Farad =

Applications of Capacitors
1. Capacitors for Energy Storage
Since the late 18th century, capacitors are used to store electrical energy. Individual capacitors do not hold a great deal of energy, providing only enough power for electronic devices to use during temporary power outages or when they need additional power. There are many applications that use capacitors as energy sources and a few of them are as follows:
- Audio equipment
- Camera Flashes
- Power supplies
- Magnetic coils
- Lasers
Supercapacitors are capacitors that have high capacitances up to 2kF. These capacitors store large amounts of energy and offer new technological possibilities in areas such as electric cars, regenerative braking in the automotive industry and industrial electrical motors, computer memory backup during power loss, and many others.
2. Capacitors for Power Conditioning
One of the important applications of capacitors is the conditioning of power supplies. Capacitors allow only AC signals to pass when they are charged blocking DC signals. This effect of a capacitor is majorly used in separating or decoupling different parts of electrical circuits to reduce noise, as a result of improving efficiency. Capacitors are also used in utility substations to counteract inductive loading introduced by transmission lines.
3. Capacitors as Sensors
Capacitors are used as sensors to measure a variety of things including humidity, mechanical strain, and fuel levels. Two aspects of capacitor construction are used in the sensing application – the distance between the parallel plates and the material between them. The former is used to detect mechanical changes such as acceleration and pressure and the latter is used in sensing air humidity.
4. Capacitors for Signal Processing
There are advanced applications of capacitors in information technology. Capacitors are used by Dynamic Random Access Memory (DRAM) devices to represent binary information as bits. Capacitors are also used in conjunction with inductors to tune circuits to particular frequencies, an effect exploited by radio receivers, speakers, and analog equalizers.
Factors Affecting Capacitance
1. Dielectric
The effect of dielectric on capacitance is that the greater the permittivity of the dielectric the greater the capacitance, likewise lesser the permittivity of the dielectric the lesser is the capacitance. Some materials offer less opposition to the field flux for a given amount of field force. Materials with greater permittivity allow more field flux, hence greater charge is collected.
2. Plate Spacing
The effect of spacing on the capacitance is that it is inversely proportional to the distance between the plates. Mathematically it is given as:
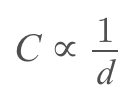
3. Area of the Plates
The effect of the area of the plate is that the capacitance is directly proportional to the area. The larger the plate area more is the capacitance value. Mathematically, it is given as C ∝ A.
 Factors Affecting Capacitance
Factors Affecting Capacitance
Capacitance of an Isolated Conductor
When a conductor is charged its potential increases. It is found that for an isolated conductor (finite-sized conductor so that potential at infinity is zero) potential of the conductor is directly proportional to the charge given to it.
q = charge on conductor
V = potential of conductor
⇒ q = CV
Where C is a proportionally constant called the capacitance of the conductor.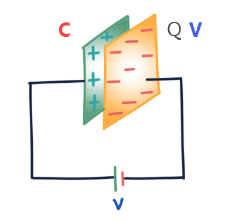
Capacitance of an isolated conductor depends on the following factors:
- Shape and size of the conductor
On increasing the size, capacitance increase. - In the surrounding medium
As the dielectric constant K increases, capacitance increases. - Presence of other conductors
When a neutral conductor is placed near a charged conductor capacitance of conductors increases.
Capacitance of a conductor does not depend on:
1. Charge on the conductor
2. Potential of the conductor
3. The potential energy of the conductor
Example 3. Find out the capacitance of an isolated spherical conductor of radius R.
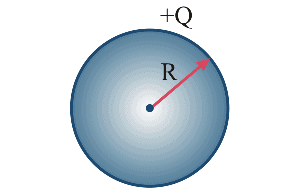
Sol. Let there is charge Q on the sphere.
Therefore, Potential V = KQ/R
Hence by the formula: Q = CV
Q = CV = (KQ)/R
C = 4πε0R
- If the medium around the conductor is a vacuum or air
Cvacuum = 4πε0R
R = Radius of the spherical conductor. (whether solid or hollow) - If the medium around the conductor is a dielectric of constant K from the surface of a sphere to infinity, then
Cmedium = 4πε0KR 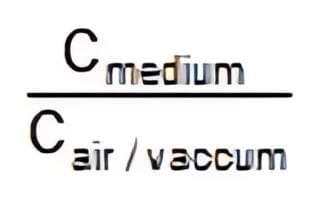 = K = dielectric constant
= K = dielectric constant
|
74 videos|314 docs|88 tests
|
FAQs on Electrostatic Potential & Capacitance - Physics Class 12 - NEET
| 1. What is a capacitor and how does it function in an electric circuit? |  |
| 2. How is capacitance defined and what factors affect it? |  |
| 3. What is electrostatic potential and how is it calculated? |  |
| 4. How do you calculate the electrostatic potential due to a system of point charges? |  |
| 5. What is the electrostatic potential due to an electric dipole and how is it expressed mathematically? |  |