Introduction: Motion in a Straight Line | Science & Technology for UPSC CSE PDF Download
Did you know that everything in the universe is always moving? Even if you are sleeping on your bed, you still belong to the Earth which is continuously moving about its axis and around the sun.
This means that you are also moving. It will be interesting for you to know that nothing in this universe is at complete rest. So it becomes very important for you to understand about motion.
In this document, we will be studying motion and its parameters in detail.
What is Frame of Reference?
In physics, a frame of reference consists of an abstract coordinate system and the set of physical reference points that uniquely fix the coordinate system and standardize measurements within that frame.
Let’s consider the following figure: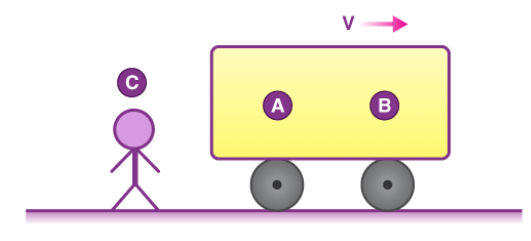
If we ask A what velocity of B is, he will say it is at rest. But if we ask the same question to C, he will say B is moving with a velocity V in the positive X direction. So we can see before specifying the velocity we have to specify in which frame we are or in simple terms, we need to define a frame of reference.
Types of Frames of Reference
1. Inertial Frame of Reference: It is the frame in which Newton's First Law of Motion holds good. This means it is a frame attached to a person at rest or in uniform motion.
2. Non-Inertial Frame of Reference: It is the frame of reference in which Newton's First law of motion does not hold. This means it is a frame attached to a person moving with variable velocity.
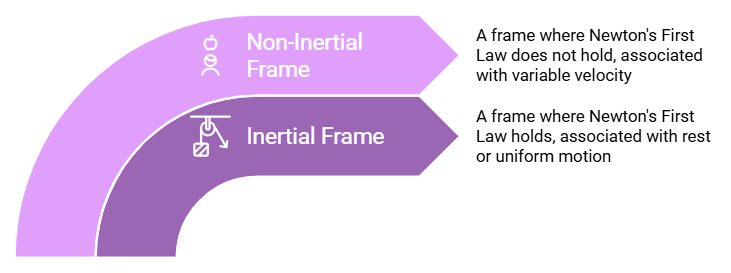 Types of Frame of References
Types of Frame of References
Point Mass Object
Generally, in physics, an object can be considered as a point mass object i.e. the distance traveled by it in motion is very large in comparison to its dimensions. Example of Point Mass Object:
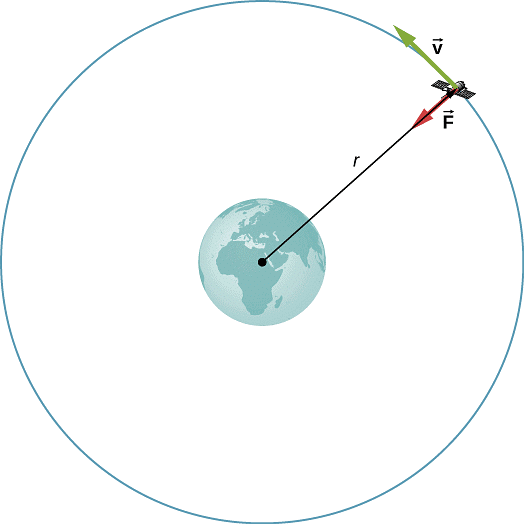 A satellite orbiting around Earth is a Point Mass Object
A satellite orbiting around Earth is a Point Mass Object
- An example of a point-mass object is a satellite orbiting around the Earth. Although satellites have physical dimensions, their motion can be effectively treated as that of a point mass. The size and shape of the satellite are insignificant compared to the vast distances it travels in space.
- By considering the satellite as a point mass, we can simplify the calculations involved in determining its trajectory, orbital speed, and gravitational interactions with other celestial bodies.
- This approximation allows for more straightforward analysis and prediction of satellite motion in orbital mechanics.
Motion and Rest
- Motion: Motion refers to the state of an object when it is changing its position with respect to a reference point or frame of reference. Objects in motion can exhibit various characteristics, including speed, direction, and acceleration.
 Motion
Motion
- Rest: Rest, on the other hand, describes the state of an object when it is not changing its position with respect to a reference point or frame of reference. An object at rest has a constant position and is not moving. In other words, its speed is zero, and it remains stationary relative to its surroundings.
- Rest and Motion are relative terms. An object may appear to be at rest in one frame of reference but in motion in another. Whether an object is considered to be at rest or in motion depends on the observer's frame of reference. In other words, there is no absolute state of rest or absolute state of motion; it's all about how you are observing the object. For e.g. a person sitting in his house is at rest w.r.t. Earth but in motion w.r.t. Moon.
Distance and Displacement
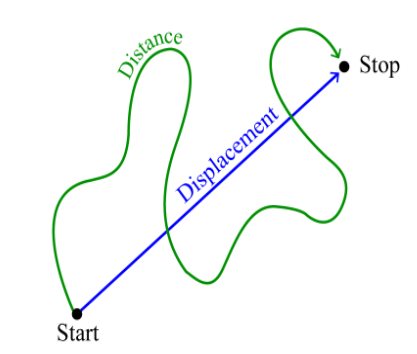
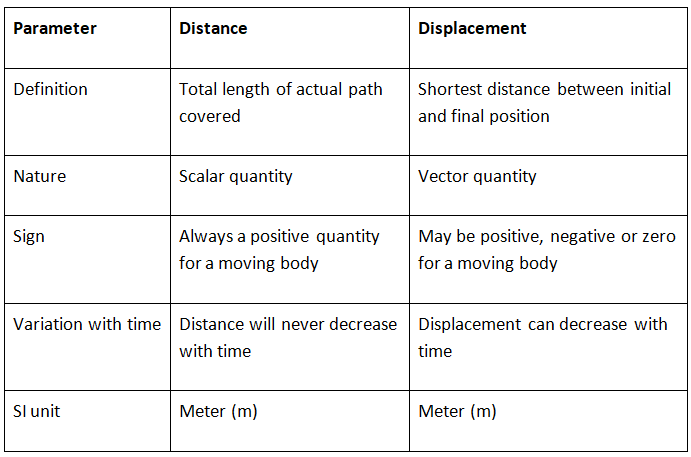
Important
- If a particle is moving in a straight line without a change in direction, the magnitude of displacement is equal to the distance traveled, otherwise, displacement is always less than distance. Thus, the numerical ratio of displacement to distance is always less than or equal to one.
- The value of displacement is always zero in case the initial point and final point of a motion are the same.
Example 1: An object moves along the grid through points A, B, C, D, E, and F as shown below. The side of the square tiles measures 0.5 km.
(a) Calculate the distance covered by the moving object.
(b) Find the magnitude of the displacement of the object.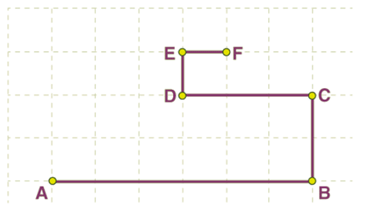
Sol: (a) The distance covered by the moving object is the length of the total path covered
AB + BC + CD + DE + EF
3 + 1 + 1.5 + 0.5 + 0.5 = 6.5 km
The distance covered by the moving object is 6.5 km.
(b) displacement is equal to the distance AF which is the shortest distance between the initial and final position.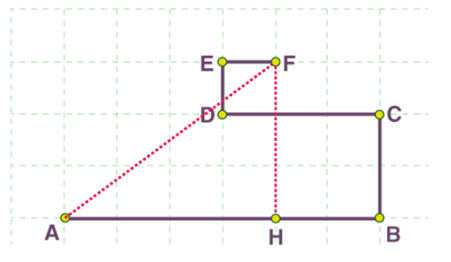
Applying the Pythagorean formula, we get,
(AF)2 = (AH)2 + (HF)2
= (4 x 0.5)2 + (3 x 0.5)2 = (2)2 + (1.5)2 = 4 + 2.25 = 6.25 km
AF = 2.5 km
Example 2: A particle moves from A to B in a circular path of radius R covering an angle θ as shown in the figure, find the ratio of the magnitude of distance and displacement of the particle.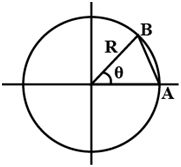
Ans: The distance traveled by the particle is the length of arc AB.
Arc length = radius x theta = Rθ
Displacement = AB
If we drop a perpendicular bisector from the center of the circle on AB we will get as shown in the figure, 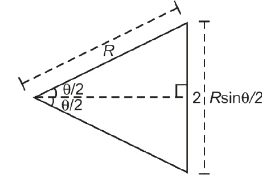
From the figure above we can conclude that, displacement = AB = 2Rsin θ/2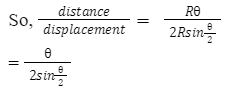
Example 3: A wheel of radius 1-meter rolls forward half a revolution on horizontal ground. What is the magnitude of the displacement of the point of the wheel initially in contact with the ground?
Sol: 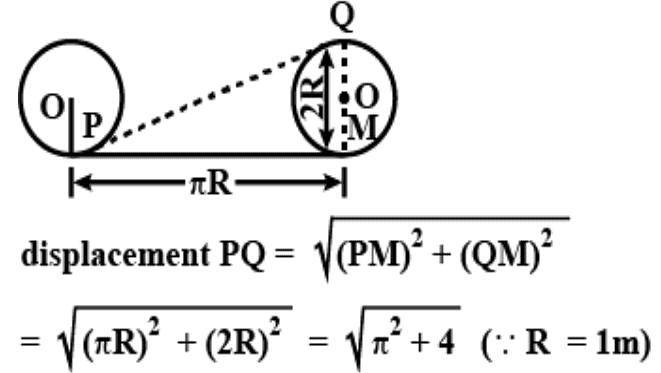
Speed and Velocity
Speed
The time rate of change of position of the object in any direction is called the speed of the object.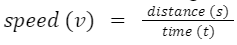
- S.I. unit is m/s.
- It is a scalar quantity.
- Its dimensional formula is [M0L1T-1].
(a) Uniform Speed
If an object covers equal distances in equal intervals of time, then its speed is called uniform speed. Such a motion is called uniform motion.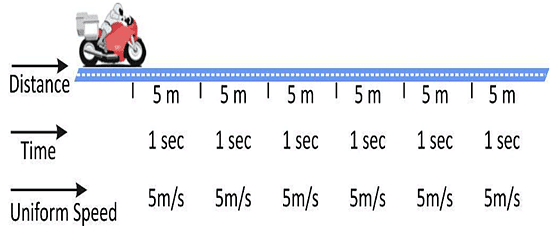
Example 4: Let's say a car travels a distance of 300 kilometers in 4 hours. Calculate the speed of the car.
Sol: In this case, the distance traveled is 300 kilometers, and the time taken is 4 hours. Plugging these values into the formula, we get: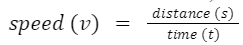
Speed = 300 km / 4 hours
Simplifying the equation, we find:
Speed = 75 km/h
Therefore, the uniform speed of the car is 75 kilometers per hour.
This means that the car is traveling at a constant rate of 75 kilometers for every hour of travel time.
(b) Average Speed
The ratio of the total distance traveled by the object to the total time taken is called the average speed of the object.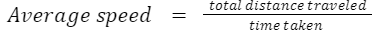
- If a particle travels distances s1, s2, s3, … with speeds v1, v2, v3, …, then,
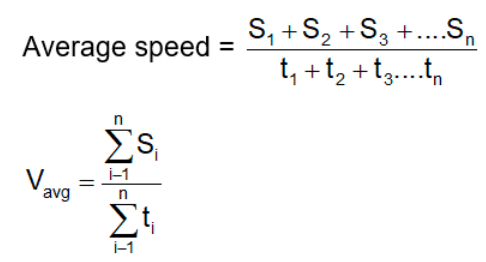
- If particle travels equal distances (s1 = s2 = s) with velocities v1 and v2, then, Average
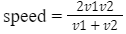
- If a particle travels with speeds v1, v2, v3, …, during time intervals t1, t2, t3,…, then, Average speed = (v1t1 + v2t2 + v3t3 +…) / (t1 + t2 + t3 +…)
- If particle travels with speeds v1, and v2 for equal time intervals, i.e., t1 = t2 = t3, then, Average speed = v1 + v2/2
- When a body travels an equal distance with speeds v1 and v2, the average speed (v) is the harmonic mean of two speeds, 2/v = 1/v1 + 1/v2

Example 5: Suppose a car travels a distance of 60 km with a speed of 40 km/h and then covers the same distance of 60 km with a speed of 60 km/h. What is the average speed of the car?
Sol: To find the average speed of the car, we use the formula:
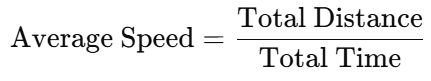
The total distance covered by the car is:
Total Distance = 60 km + 60 km = 120 km.
Time for the first segment (60 km at 40 km/h):
Time for the second segment (60 km at 60 km/h):
t2 = Distance/Speed = 60/60 = 1 hour.
Total Time = t1+ t2 = 1.5 + 1 = 2.5 hours.

Example 6: A particle moving in a straight line traveled half of the distance with a speed V0. The remaining part of the distance is covered with a speed V1 for half of the time and with a speed V2 for the other half of the time. The average speed of the particle over the whole time of the motion is
Sol: 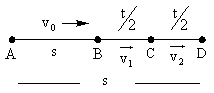
Given that
A particle covered the journey from A to D = 2s
It covered A to B i.e. = s
With speed =v0
Time taken 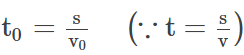
It covered B to D i.e. = 2s
In time = t
Such that 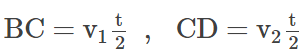
We get
BD = BC + CD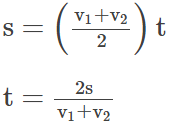
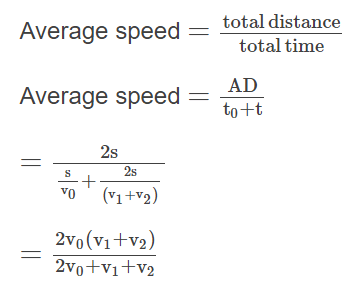
Example 7: A man walks on a straight road from his home to a market 2.5 km away with a speed of 5 km/h. Finding the market closed, he instantly turns and walks back home at a speed of 7.5 km/h. If the total time of travel is 40 min, find the average speed of the man for the whole journey.
Sol: Given data
Distance between the home and market = 2.5 km
Total time of travel = 40 min
Speed = 5 km/h and 7.5 km/h
Finding the average speed
From home to market, the time taken is time = d/v = 2.5/5 = 1/2 hr = 30min.
He returns with a speed of 7.5 km/h for the rest of the time, that is, 10 minutes.
(40 min is the total time to travel and 30 min is the time taken to go to market so the remaining time is 10 min.)
Distance = 7.5 × 10/60 = 1.25km
Average speed = Total distance/Total time
The distance is given as:
km
The time is given as hours, which is equivalent to:
hours
Calculate average speed:
Hence the average speed is 5.625 km/h
(c) Non-Uniform or Variable Speed
If an object covers unequal distances in equal intervals of time, then its speed is called non-uniform or variable speed. Such a motion is called a non-uniform motion. In the data shown below, the distance traveled by the body is unequal in equal time intervals.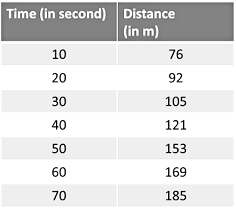
Example 8: Let's consider a car moving along a curved track. The car starts from rest and increases its speed uniformly to 20 m/s over a distance of 100 meters. After reaching this speed, it reduces its speed uniformly and comes to a stop over a distance of 50 meters. Find the average speed of the car during this entire motion.
Sol: To find the average speed of the car during this entire motion, we can use the formula:
Average Speed = Total Distance / Total Time
First, let's calculate the time taken for the acceleration phase:
Using the equation of motion:
v2 = u2 + 2as, where v is the final velocity, u is the initial velocity, a is the acceleration, and s is the distance.
(We will discuss the equation of motion later in this document)
202 = 02 + 2a(100)
400 = 200a
a = 400/200
a = 2 m/s2
The time taken for the acceleration phase can be calculated using the equation:
v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time.
20 = 0 + 2t
t = 20/2
t = 10 seconds
Now, let's calculate the time taken for the deceleration phase:
Using the same equation of motion:
v2 = u2 + 2as, where v is the final velocity, u is the initial velocity, a is the acceleration, and s is the distance.
02 = 202 + 2a(50)
0 = 400 - 100a
100a = 400
a = 400/100
a = 4 m/s2
The time taken for the deceleration phase can be calculated using the equation: v = u + at, where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time.
0 = 20 + (-4)t
4t = 20
t = 20/4
t = 5 seconds
Now, let's calculate the total time for the motion:
Total Time = Time for acceleration + Time for deceleration
Total Time = 10 seconds + 5 seconds
Total Time = 15 seconds
Finally, we can calculate the average speed using the formula:
Average Speed = Total Distance / Total Time
Total Distance = Distance during acceleration + Distance during deceleration
Total Distance = 100 meters + 50 meters
Total Distance = 150 meters
Average Speed = 150 meters / 15 seconds
Average Speed = 10 m/s
Therefore, the average speed of the car during this non-uniform motion is 10 m/s.
Velocity
The rate of change of displacement of an object in a particular direction is called its velocity.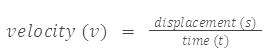
- Its dimensional formula is [M0 L1T -1].
- Its unit is m/s.
- It is a vector quantity, as it has both, the magnitude and direction.
- The velocity of an object can be positive, zero or negative.
Example 9: Let's say a car travels a distance of 150 kilometers in 2 hours. Find the velocity of the car.
Sol: In this case, the displacement is 150 kilometers, and the time taken is 2 hours. Plugging these values into the formula: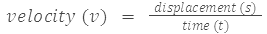
velocity = 150 km / 2 h = 75 km/h.
Therefore, the velocity of the car is 75 kilometers per hour.
Example 10: A car travels from point A to B in 3 hours and returns back to point A in 5 hours. Points A and B are 150 miles apart along a straight highway. What is the velocity of the car?
Sol: The velocity of the car is zero in this case as displacement is zero (initial and final positions are the same).
(a) Uniform Velocity
If an object undergoes equal displacements in equal intervals of time, then it is said to be moving with a uniform velocity.
Important
This is only possible in the case where a body is traveling in a straight line without changing its direction.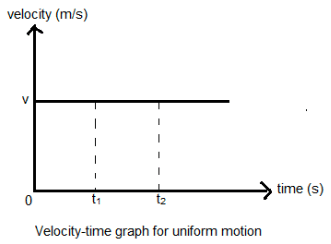
(b) Non-Uniform or Variable Velocity
If an object undergoes unequal displacements in equal intervals of time, then it is said to be moving with a non-uniform or variable velocity.
Important: This is possible only if the body changes the magnitude of speed or its direction w.r.t. Time.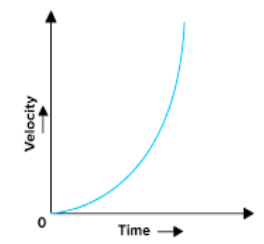
(c) Average Velocity
The ratio of the total displacement to the total time taken is called average velocity.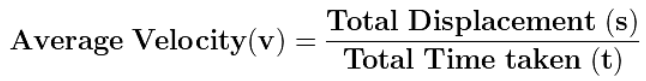
Example 11: Suppose a hiker starts at point A and walks 10 kilometers to point B in 2 hours. After a short break at point B, the hiker continues walking for another 6 kilometers to reach point C in 1.5 hours. To find the average velocity for the entire journey, we can use the formula:
Sol: Average velocity = total displacement / total time taken.
The total displacement is the sum of the individual displacements, which is 10 kilometers + 6 kilometers = 16 kilometers.
The total time taken is the sum of the individual times, which is 2 hours + 1.5 hours = 3.5 hours.
Plugging these values into the formula:
average velocity = 16 km / 3.5 h ≈ 4.57 km/h.
Therefore, the average velocity for the entire journey is approximately 4.57 kilometers per hour.
Example 12: Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes 50 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging (a) from A to B and (b) from A to C?
Sol: (a) From A to B
Total distance covered from A to B = 300 m
Total displacement = 300m
Total time taken = 2 × 60 s + 50 s = 170 s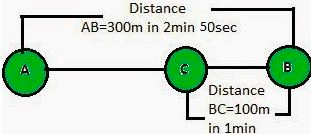
Therefore, average speed from A to B = Total Distance/Total Time = 300/170 = 1.76ms−1
Average velocity from A to B = Displacement AB/Time = 1.76ms−1
(b) From A to C
Total distance covered from A to C = AB + BC = 300 + 100 m = 400 m
Total time taken from A to C = = 170 s + 60 s = 230 s
Therefore, average speed from A to C = Total Distance/Total Time = 400/230−1 =1.74ms−1
Displacement from A to C = AC= AB - BC = 300 - 100 = 200 m
Time taken for displacement from A to C = 230 s
Therefore, average velocity from A to C = Displacement /Time = 200/230ms−1 = 0.87ms−1
Example 13: An insect crawls a distance of 4m along the north in 10 s and then a distance of 3m along the East in 5 s. What is the average velocity of the insect?
Sol: 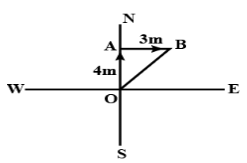
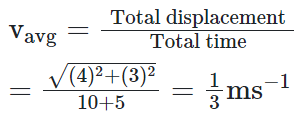
Important
Often we use the terms speed and velocity interchangeably without realizing it is wrong to do so. There is a difference between speed and velocity which everyone must know. Below is the difference between these two terms.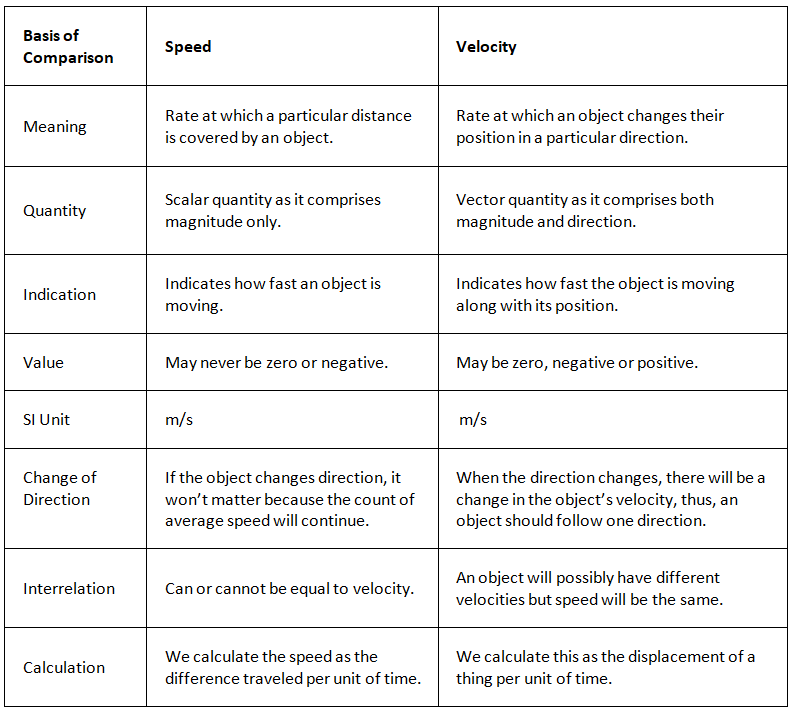
Acceleration
The time rate of change of velocity is called acceleration.
- Its unit is m/s2
- Its dimensional formula is [M0LT-2].
- It is a vector quantity.
Acceleration can be positive, zero, or negative. A positive acceleration means velocity increases with time, zero acceleration means velocity is uniform while negative acceleration (retardation) means velocity is decreasing with time.
If a particle is accelerated for a time t1 with acceleration a1 and for a time t2 with acceleration a2.
Then the average acceleration: aav = (a1t1 + a2t2 ) / (t1 + t2)
Example 14: Suppose a car initially at rest accelerates uniformly and reaches a final velocity of 30 m/s after 6 seconds. To find the average acceleration of the car, we can use the formula:
Sol: Average Acceleration = (final velocity - initial velocity) / time.
In this case, the initial velocity is 0 m/s, the final velocity is 30 m/s, and the time taken is 6 seconds. Plugging these values into the formula:
average acceleration = (30 m/s - 0 m/s) / 6 s = 5 m/s2.
Uniformly Accelerated Motion
Uniformly accelerated motion refers to the motion of an object that is experiencing a constant acceleration. In this type of motion, the object's velocity changes at a constant rate over time.
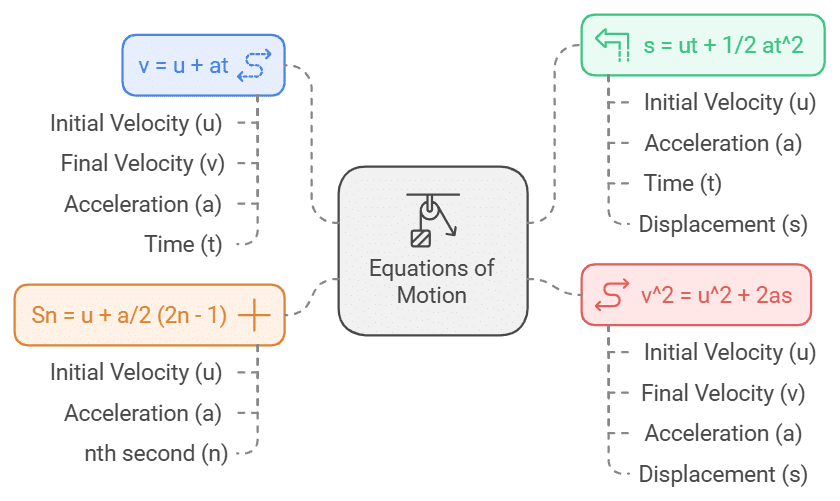
Equations of Motion
If a body starts with velocity (u) and after time t its velocity changes to v, if the uniform acceleration is a and the distance traveled in time t in s, then the following relations are obtained, which are called equations of uniformly accelerated motion.
(i) v = u + at
- v represents the final velocity of an object.
- u represents the initial velocity of an object.
- a represents the constant acceleration experienced by the object.
- t represents the time taken for the object to undergo the acceleration.
(ii) s = ut + 1/2 at2
- s represents the displacement or distance traveled by an object.
- u represents the initial velocity of the object.
- a represents the constant acceleration experienced by the object.
- t represents the time taken by the object.
(iii) v2 = u2 + 2as
- v represents the final velocity of an object.
- u represents the initial velocity of the object.
- a represents the constant acceleration experienced by the object.
- s represents the displacement or distance traveled by the object.
(iv) Distance traveled in nth second Sn = u + a/2 (2n – 1)
- Sn represents the distance traveled during the nth second.
- u represents the initial velocity of the object.
- a represents the constant acceleration experienced by the object.
- n represents the time in seconds, specifically the nth second of motion.
If a body moves with uniform acceleration and velocity changes from u to v in a time interval, then the velocity at the midpoint of its path.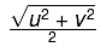
Here are some numerical examples for the above equations:
(i) v = u + at:
Example 15: Let's say a car starts from rest (initial velocity u = 0) and accelerates at a rate of 2 m/s2 for 5 seconds. We can calculate the final velocity (v) using the equation:
v = u + at
v = 0 + (2 m/s2)(5 s) = 10 m/s
Therefore, the final velocity of the car after 5 seconds of acceleration is 10 m/s.
(ii) s = ut + 1/2at2:
Example 16: Consider a ball that is thrown upwards with an initial velocity of 20 m/s. If we want to find the displacement (s) of the ball after 3 seconds, we can use the equation:
s = ut + 1/2at2
s = (20 m/s)(3 s) + 1/2(-9.8 m/s2)(3 s)2 ≈ 15 m
Hence, the ball has a displacement of approximately 15 meters after 3 seconds.
(iii) v2 = u2 + 2as:
Example 16: Suppose a body starts from rest (initial velocity u = 0) and experiences a constant acceleration of 4 m/s2. If we want to find the final velocity (v) after covering a distance of 100 meters, we can use the equation:
v2 = u2 + 2as
v2 = 02 + 2(4 m/s2)(100 m) = 800 m2/s2
Taking the square root of both sides, we get:
v ≈ 28.28 m/s
Therefore, the final velocity of the body after covering a distance of 100 meters is approximately 28.28 m/s.
(iv) Distance traveled in nth second Sn = u + a/2(2n – 1):
Example 17: Let's say an object is moving with an initial velocity of 10 m/s and an acceleration of 2 m/s2. We want to find the distance traveled during the 4th second. We can use the formula:
Sn = u + a / 2(2n – 1)
S4 = 10 m/s + (2 m/s2) / 2(2(4) – 1)
S4 = 10 m/s + 1 (7)
S4 = 17 m
Hence, the distance traveled during the 4th second is 17 meters.
Motion Under Gravity
The force of attraction of earth on bodies is called the force of gravity. Acceleration produced in the body by the force of gravity is called acceleration due to gravity. It is represented by the symbol g. In the absence of air resistance, it is found that all bodies (irrespective of size, weight, or composition) fall with the same acceleration near the surface of the earth. This motion of a body falling towards the earth from a small altitude (h<<R) is called free fall. (1) If a body drops from some height, taking an initial position as the origin and direction of motion (i.e., downward direction) as a positive, here we have:
If the initial velocity is zero, then u = 0.
Graph of distance velocity and acceleration with respect to time: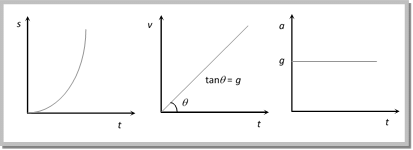
(3) If a body is projected vertically upward, taking an initial position as origin and direction of motion (i.e., vertically up) as positive then,
a=-g [As acceleration is downwards while motion upwards]
So, if the body is projected with velocity u and after time t it reaches up to height s then,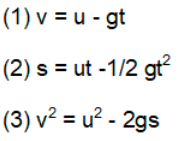
Graph of distance, velocity, and acceleration with respect to time (for maximum height):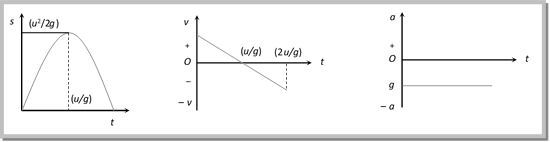
It is clear that both quantities do not depend upon the mass of the body or we can say that in the absence of air resistance, all bodies fall on the surface of the earth at the same rate. Here are some numerical examples for the above equations:
Example 18: Freely falling object (u = 0) under gravity:
(i) v = u + gt:
Consider an object falling freely under gravity with an acceleration of g = 9.8 m/s2. If we want to find the final velocity (v) after 3 seconds of free fall, we can use the equation:
v = u + gt
v = 0 + (9.8 m/s2)(3 s)
v = 29.4 m/s
(ii) h = ut + 1/2gt2:
To determine the height (h) traveled by the object during the 3 seconds of free fall, we can use the equation:
h = ut + 1/2gt2
h = 0 + 1/2(9.8 m/s2)(3 s)2
h = 44.1 m
(iii) v2 = u2 + 2gh:
Using the equation to find the square of the final velocity (v) of the freely falling object:
v2 = u2 + 2gh
v2 = 02 + 2(9.8 m/s2)(44.1 m)
v2 = 862.68 m2/s2
v ≈ 29.38 m/s
Example 19: Object thrown upward: If an object is thrown upward, the acceleration due to gravity (g) is replaced by (-g) in the equations of motion. Let's consider the same initial conditions and time values as in Example 1:
(i) v = u + (-g)t:
Using the equation for the final velocity (v) of the object thrown upward:
v = u + (-g)t
v = 0 + (-9.8 m/s2)(3 s)
v = -29.4 m/s
(ii) h = ut + 1/2(-g)t2:
To calculate the height (h) reached by the object thrown upward during the 3 seconds, we use the equation:
h = ut + 1/2(-g)t2
h = 0 + 1/2(-9.8 m/s2)(3 s)2
h = -44.1 m
(Note: The negative sign indicates that the object is below the starting point.)
(iii) v2 = u2 + 2(-g)h:
Applying the equation for the square of the final velocity (v) of the object thrown upward:
v2 = u2 + 2(-g)h
v2 = 02 + 2(-9.8 m/s2)(-44.1 m)
v2 = 862.68 m2/s2
v ≈ 29.38 m/s
These examples illustrate how the equations of motion can be used to analyze the motion of freely falling objects and objects thrown upward under the influence of gravity.
Non- Uniformly Accelerated Motion
Non-uniformly accelerated motion refers to the motion of an object that is changing its velocity at a non-constant rate. In other words, the object is accelerating or decelerating, but the acceleration itself is not constant over time. This type of motion can be more complex to analyze than uniformly accelerated motion, where the acceleration remains constant. To understand this kind of motion, one must know about Instantaneous velocity.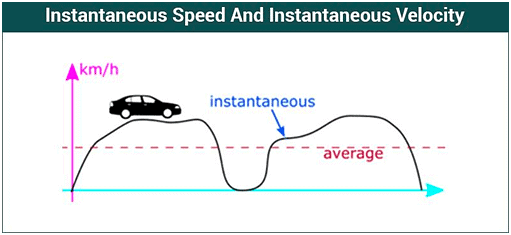
When an object is traveling with variable velocity, its speed at a given instant of time is called its instantaneous velocity.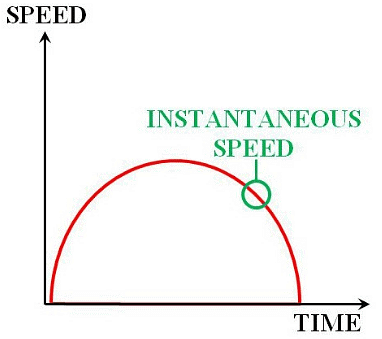
Example 20: Let's say a car is traveling along a straight road, and its position is given by the equation: x(t) = 3t2 - 2t + 1, where x is the position of the car at time t. Find the instantaneous speed of the car at a specific time t.
Sol: To find the instantaneous speed of the car at a specific time t, we need to calculate the derivative of the position function with respect to time. The derivative will give us the rate of change of position, which is the velocity.
Differentiating x(t) with respect to t, we get: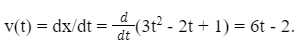
Now, to find the instantaneous speed at a particular time, substitute the value of t into the velocity function.
Let's say we want to find the instantaneous speed at t = 2 seconds:
v(2) = 6(2) - 2 = 12 - 2 = 10 m/s.
Therefore, the instantaneous speed of the car at t = 2 seconds is 10 m/s.
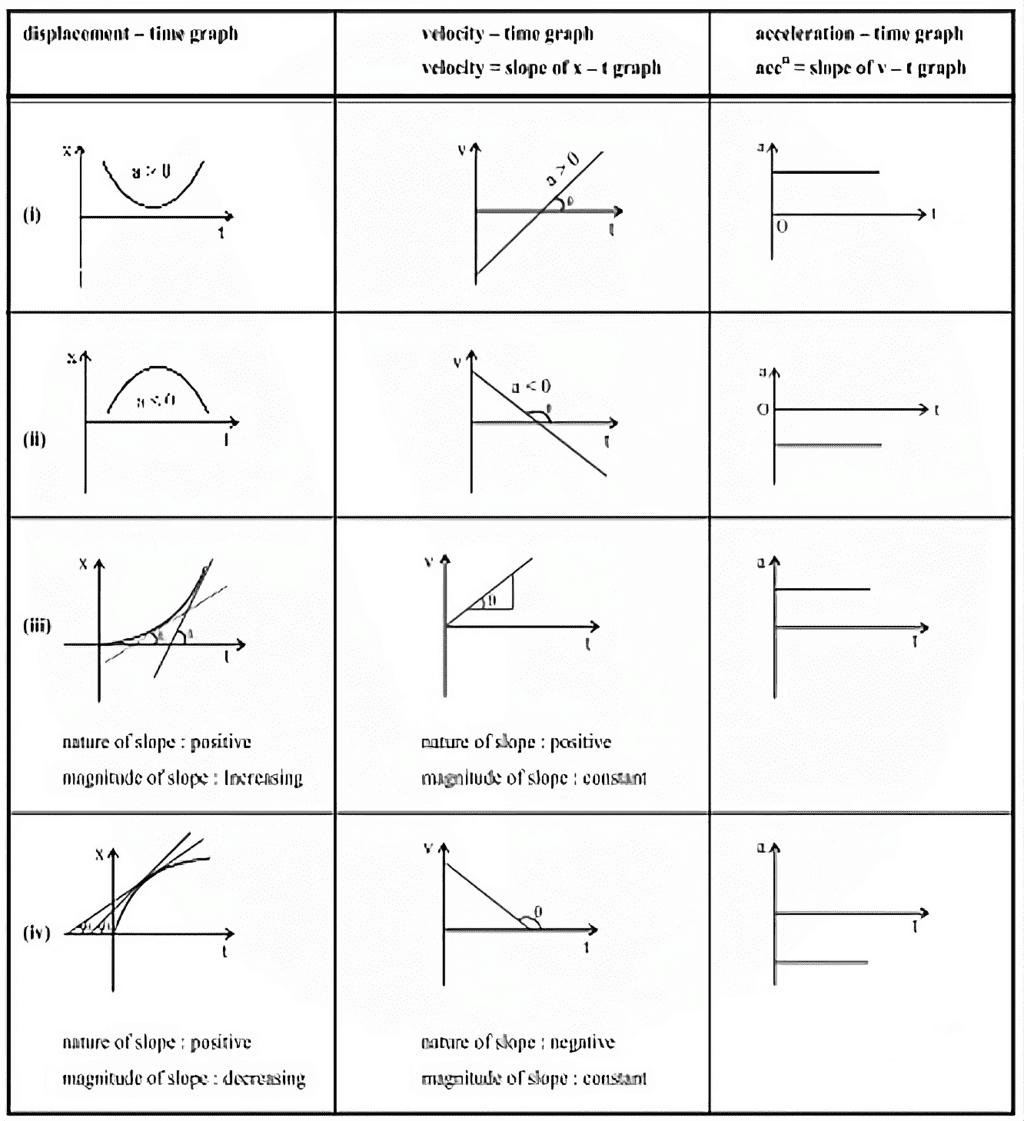
Graphs Related To Kinematics
(i) Uniform Motion
(ii) Non Uniform Motion
Relative Motion in 1-D
The relative velocity of one object with respect to another object is the time rate of change of the relative position of one object with respect to another object.
The relative velocity of object A with respect to object B
VAB = VA – VB
- When two objects are moving in the same direction, then
VAB = VA - VB
or
VAB = VA - VB
- When two objects are moving in the opposite direction, then
VAB = VA + VB
or
VAB = VA + VB
- When two objects are moving at an angle, then
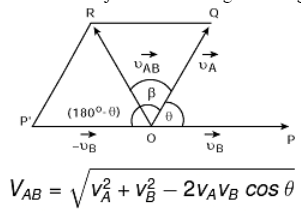
and tan β = vB sin θ / vA – vB cos θ
Example 21 : Let's consider two cars, Car A and Car B, traveling in the same direction along a straight road. Car A is moving at a speed of 60 km/h, while Car B is moving at a speed of 80 km/h.
Sol: To determine the relative velocity of Car B with respect to Car A, we subtract the velocity of Car A from the velocity of Car B.
Relative velocity of Car B with respect to Car A = Velocity of Car B - Velocity of Car A
Relative velocity = 80 km/h - 60 km/h = 20 km/h.
Therefore, the relative velocity of Car B with respect to Car A is 20 km/h. This means that Car B is moving 20 km/h faster than Car A in the same direction.
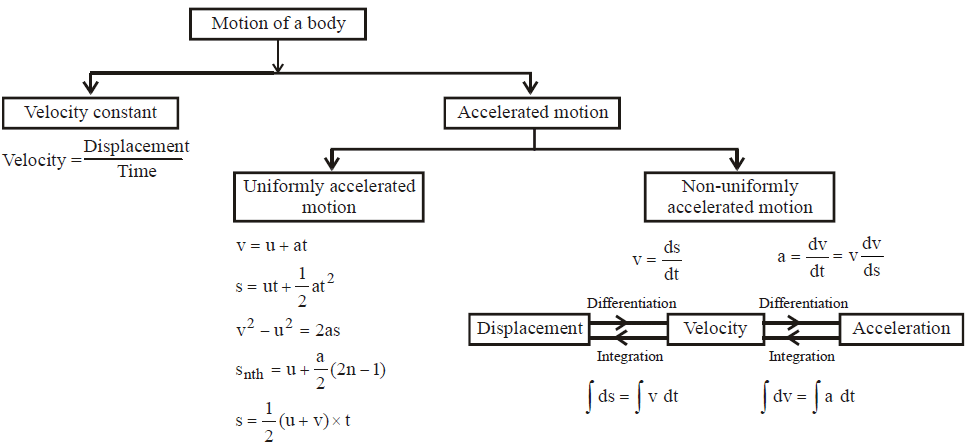
Summary
|
90 videos|491 docs|209 tests
|
FAQs on Introduction: Motion in a Straight Line - Science & Technology for UPSC CSE
| 1. What is the significance of the frame of reference in understanding motion? |  |
| 2. How do distance and displacement differ in kinematics? |  |
| 3. What is the relationship between speed and velocity? |  |
| 4. What is uniformly accelerated motion, and how is it characterized? |  |
| 5. How does motion under gravity differ from other types of motion? |  |

















