Introduction: Relations & Functions | Mathematics (Maths) for JEE Main & Advanced PDF Download
| Table of contents |

|
| What is a Relation? |

|
| What is Empty and Universal Relation? |

|
| What are Reflexive, Symmetric and Transitive Relation? |

|
| Types of functions : |

|
What is a Relation?
Relation is a subset of Cartesian product.
Let us take an example . Let A = {Kualalumpur, Jakarta, Canberra, Washington DC} and B={Malaysia, Indonesia, Australia, USA}. We define relation as R= {(x,y): x is the first letter of y, x ∈ A ,y ∈ B}. So, our relation R is R = {(Kualalumpur, Malaysia), (Jakarta, Indonesia), (Canberra, Australia), (Washington DC, USA)}
Representing relations with arrow is called arrow diagram.
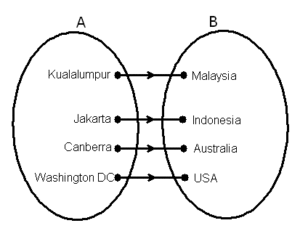
Now, in our relation Domain is set of all first elements in R. Domain = {Kualalumpur, Jakarta, Canberra, Washington DC}. You should note that Domain ≠ A. Range is set of all second elements in R. Range ={Malaysia, Indonesia, Australia, USA}.Codomain is second set. Codomain= Q ={Malaysia, Indonesia, Australia,USA.
What is Empty and Universal Relation?
Empty Relation: A Relation is called empty relation if Relation has no elements. Hence, we write R = ∅Universal Relation: If Relation has all the elements then it is known as Universal Relation. Now, let us take an example:
Let A= Set of all students in a boys school. We define relation R on set A as R = {(a, b): a and b are sisters} and R’ = {(a, b): height of a and b is greater than 10 cm}.Now,
R = {(a, b ): a and b are sisters}. It is a boys school, so there are no girls in the school. Hence, there cannot be a sister. Therefore, R has no elements. R = ∅ that is R is an empty relation
R’ = { (a, b); height of both a and b is greater than 1 cm}. Height of children is always greater than 10 cm.Thus, height of a and b will always be greater than 10 cm. Therefore, R has all the students of the school. Hence, R is a universal relation, because it has all the elements.
What are Reflexive, Symmetric and Transitive Relation?
Equivalence relation is one of the most important relation that plays a significant role in Mathematics. To study equivalence relation, we first have to consider three types of relations, namely reflexive, symmetric and transitive.- If there is a relation R in set A then a relation will be reflexive if (a, a ) ∈ R for every a ∈A.
- The relation will be symmetric if (a, b ) ∈ R for every (b ,a) ∈ A.
- Similarly, a relation will be transitive if (a, b ) ∈ and (b ,c) ∈ R then (a, c ) ∈ R.
If relation is reflexive, symmetric and transitive then it is an equivalence relation. Let us now look at an example.
Example 1: Let us define Relation R on Set A = {1, 2, 3}. Now, let us check reflexive, symmetric and transitive relation in this.
Solution: R = {(1 , 1),(2 , 2),(3 , 3),(1, 2),(2 , 3), (1 , 3)}
Check Reflexive:
If the relation is reflexive , then (a , a) ∈ R for every a ∈ {1,2,3}. Since (1 , 1) ∈ R , (2 , 2 ) ∈ R and (3 , 3) ∈ R. Therefore, R is reflexive.
Check Symmetric:
To check whether a relation is symmetric or not, if (a , b) ∈ R, then (b , a) ∈ R. Here,(1 , 2) ∈ R , but (2 , 1) ∉ R.Therefore, R is not symmetric.
Check Transitive:
To check whether a relation is transitive or not, if (a, b ) ∈ R and (b ,c) ∈ R then (a , c ) ∈ R. Here, as you can see that if (1, 2 ) ∈ R and (2 ,3) ∈ R then (1 , 3 ) ∈ R. Therefore, R is transitive.
What is Function?
A relation from A to B is a function if every element of set A has one and only one image in set B. Therefore, for a function,
Every element of set A will have an image.
Every element of set A will have only have one image in set B.
Let us take an example now. Let A = {1, 2, 3, 4, 5} and B= {2, 4, 6, 8, 1}
As we have discussed above that for every element of set A will have an image. And we can see that elements 4 and 6 does not have any image. Also,every element of set A should have only one image in set B but as you can see that elements 2,3 and 4 have same image,6. Therefore, it is not a function.
Note: In a function, domain will always be equal to first set.
Example 1: Is the relation expressed in the mapping diagram a function?
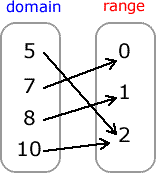
Each element of the domain is being traced to one and only element in the range. However, it is okay for two or more values in the domain to share a common value in the range. That is, even though the elements 5 and 10 in the domain share the same value of 2 in the range, this relation is still a function.
Example 2: Is the relation expressed in the mapping diagram a function?
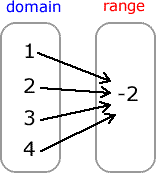
What do you think? Does each value in the domain point to a single value in the range? Absolutely! There’s nothing wrong when four elements coming from the domain are sharing a common value in the range. This is a great example of a function as well.
Example 3: Is the relation expressed in mapping diagram a function?
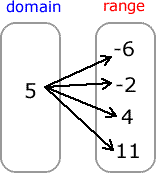
If you think example 3 was “bad”, this is “worse”. A single element in the domain is being paired with four elements in the range. Remember, if an element in the domain is being associated with more than one element in the range, the relation is automatically disqualified to be a function. Thus, this relation is absolutely not a function.
Example 4: Is the mapping diagram a relation, or function?
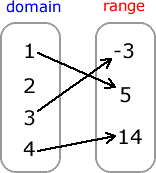
Let me throw in this example to highlight a very important idea. Your teacher may give something like this just to check if you pay attention to details.
So far it looks normal. But there’s a little problem. The element “2” in the domain is not being paired with any element in the range. Every element in the domain must have some kind of correspondence to the range for it be considered a relation at least. Since this is not a relation, it follows that it can’t be a function.
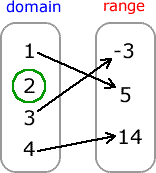
So, the final answer is neither a relation nor a function.
Types of functions :
There are three types of function: one-one function, many-one function and onto function. Let us talk about them in detail.1. One – One Function: This function is also known as injective. F: X → Y. Function is one-one if every element has a unique image, that is when f( x1 ) = f( x2 ).Hence, x1 = x2 .Otherwise the function is many–one.
How to check if function is one-one (Method 1)
In this method, we will check for each and every element manually if it has unique image.
Ques 1: Check if the following is a one-one function ?
| Element | Image |
| a1 | b1 |
| a2 | b2 |
| a3 | b3 |
| a4 | b4 |
Since, every element has a unique image, it is one-one function.
Ques 2:
| Element | Image |
| 1 | 2 |
| 2 | 6 |
| 3 | 6 |
| 4 | 6 |
| 5 | 1 |
Since, element 2, 3 and 4 have same images, it is not one-one function , it ismany-one function.
How to check if function is one-one (Method 2)
This method can be used if there are large numbers. For example, if
f : N → N (There are infinite number of natural numbers).
f : R → R (There are infinite number of real numbers).
f : Z → Z (There are infinite number of integers)
Solution:
Step 1: Calculate f( x1 )
Step 2: Calculate f( x2)
Step 3: Put f( x1 ) = f( x2 ).
If x1 = x2 , then it is one-one function otherwise it will be many-one function.
2. Onto Function: This function is also known as surjective function.
f : X → Y. Function f is onto if every element of set Y has a pre-image in set X that is for every y ∈ Y, there is x ∈ X such that f( x ) = y.
How to check if function is onto (Method 1)
Ques 1: Check whether the following is an onto function?
Solution: Since all elements of set B has a pre-image in set A , it is onto function.
Ques 2: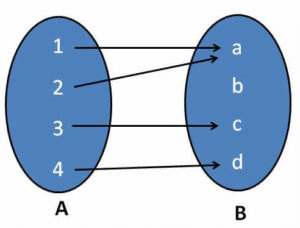
Solution: Since element b has no pre-image, it is not a onto function.
How to check if function is onto (Method 2)
This method is also used if there are large numbers. For instance, if
f : N → N (There are infinite number of natural numbers)
f : R → R (There are infinite number of real numbers)
f : Z → Z (There are infinite number of integers)
Solution: How to check onto?
Step 1: Put y= f( x )
Step 2: Find x in terms of y.
If X ∈ X , then f is onto.
Many to One Function
It is a function which maps two or more elements of A to the same element of set B. Two or more elements of A have the same image in B.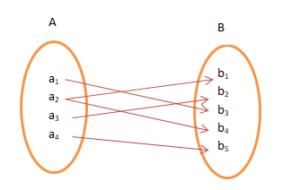
What is Bijective Function?
A function f : X → Y is said to be bijective function if it is both one-one and onto.
Ques 1: Check whether the following is a bijective function?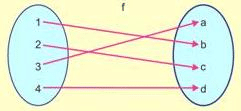
Solution: As you can see that all the elements have a unique image and also all the elements have a pre-image in set A. Hence, function is both one-one and onto. Therefore, it is bijective function.
Ques 2: Find if the following is bijective function?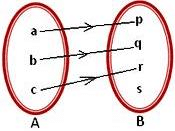
Solution: Function is one-one since every element of set A has unique image in set B but not onto because ‘s’ do not have a pre-image in set A. Hence, it is not bijective function.
|
172 videos|501 docs|154 tests
|
FAQs on Introduction: Relations & Functions - Mathematics (Maths) for JEE Main & Advanced
| 1. What is a relation? |  |
| 2. What is an empty relation? |  |
| 3. What is a universal relation? |  |
| 4. What is a reflexive relation? |  |
| 5. What is a transitive relation? |  |
















