Irodov Solutions: Liquids Capillary Effects | Physics Class 11 - NEET PDF Download
Q. 160. Find the capillary pressure
(a) in mercury droplets of diameter d = 1.5 pm;
(b) inside a soap bubble of diameter d = 3.0 mm if the surface tension of the soap water solution is α = 45 mN/m.
Solution. 160.
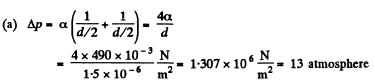
(b) The soap bubble has two surfaces
so 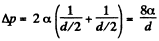
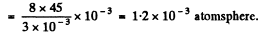
Q. 161. In the bottom of a vessel with mercury there is a round hole of diameter d = 70 μm. At what maximum thickness of the mercury layer will the liquid still not flow out through this hole?
Solution. 161. The pressure just inside the hole will be less than the outside pressure by 4 α/d. This can support a height h of Hg where
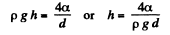
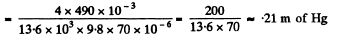
Q. 162. A vessel filled with air under pressure P0 contains a soap bubble of diameter d. The air pressure having been reduced isothermally n-fold, the bubble diameter increased η-fold. Find the surface tension of the soap water solution.
Solution. 162. By Boyle's law
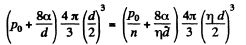
or 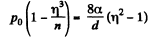
Thus 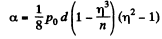
Q. 163. Find the pressure in an air bubble of diameter d = 4.0 μm, located in water at a depth h = 5.0 m. The atmospheric pressure has the standard value P0.
Solution. 163. The pressure has terms due to hydrostatic pressure and capillarity and they add
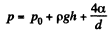
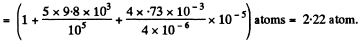
Q. 164. The diameter of a gas bubble formed at the bottom of a pond is d = 4.0 μm. When the bubble rises to the surface its diameter increases n = 1.1 times. Find how deep is the pond at that spot. The atmospheric pressure is standard, the gas expansion is assumed to be isothermal.
Solution. 164. By Boyle's law
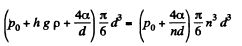
or 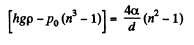
or 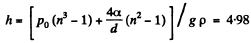 meter of water
meter of water
Q. 165. Find the difference in height of mercury columns in two communicating vertical capillaries whose diameters are d1 = 0.50 mm and d2 = 1.00 mm, if the contact angle θ = 138°.
Solution. 165. Clearly
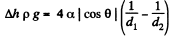
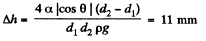
Q. 166. A vertical capillary with inside diameter 0.50 mm is submerged into water so that the length of its part protruding over the water surface is equal to h = 25 mm. Find the curvature radius of the meniscus.
Solution. 166. In a capillary with diameter d = 0.5 mm water will rise to a height
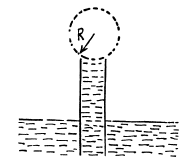
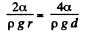
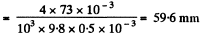
Since this is greater than the height (= 25 mm) of the tube, a meniscus of radius R will be formed at the top of the tube, where
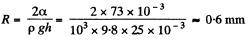
Q. 167. A glass capillary of length l = 110 mm and inside diameter d = 20 μm is submerged vertically into water. The upper end of the capillary is sealed. The outside pressure is standard. To what length x has the capillary to be submorged to make the water levels inside and outside the capillary coincide?
Solution. 167. Initially the pressure of air in the cppillary is p0 and it’s length is Z. When submerged under water, the pressure of air in the portion above water must be 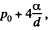 since the level of water inside the capillary is the same as the level outside. Thus by Boyle’s law
since the level of water inside the capillary is the same as the level outside. Thus by Boyle’s law
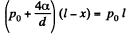
or 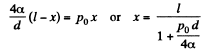
Q. 168. When a vertical capillary of length l with the sealed upper end was brought in contact with the surface of a liquid, the level of this liquid rose to the height h. The liquid density is p, the inside diameter of the capillary is d, the contact angle is θ, the atmospheric pressure is P0. Find the surface tension of the liquid.
Solution. 168. We have by Boyle’s law
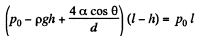
or, 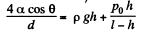
Hence, 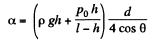
Q. 169. A glass rod of diameter d1 = 1.5 mm is inserted symmetrically into a glass capillary with inside diameter d2 = 2.0 mm. Then the whole arrangement is vertically oriented and brought in contact with the surface of water. To what height will the water rise in the capillary?
Solution. 169. Suppose the liquid rises to a height h. Then the total energy of the liquid in the capillary is
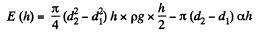
Minimising E we get
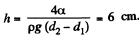
Q. 170. Two vertical plates submerged partially in a wetting liquid form a wedge with a very small angle δφ. The edge of this wedge is vertical. The density of the liquid is p, its surface tension is α, the contact angle is θ. Find the height h, to which the liquid rises, as a function of the distance x from the edge.
Solution. 170. Let h be the height of the water level at a distance x from the edge. Then the total eneigy of water in the wedge above the level outside is.
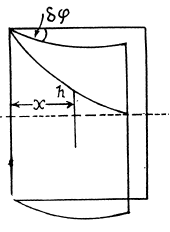
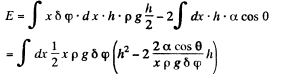
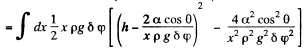
This is minimum when 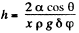
Q. 171. A vertical water jet flows out of a round hole. One of the horizontal sections of the jet has the diameter d = 2.0 mm while the other section located l = 20 mm lower has the diameter which is n = 1.5 times less. Find the volume of the water flowing from the hole each second.
Solution. 171. From the equation of continuity
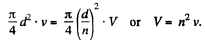
We then apply Bernoulli’s theorem
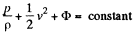
The pressure p differs from the atmospheric pressure by capillary effects. At the upper section
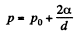
neglecting the curvature in the vertical plane. Thus,
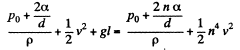
or 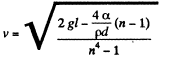
Finally, the liquid coming out per second is,
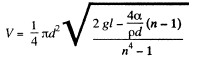
Q. 172. A water drop falls in air with a uniform velocity. Find the difference between the curvature radii of the drop's surface at the upper and lower points of the drop separated by the distance h = 2.3 mm.
Solution. 172. The radius of curvature of the drop is R1 at the upper end of the drop and R2 at the lower end. Then the pressure inside the drop is 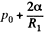 at the top end and
at the top end and 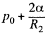 at the bottom end. Hence
at the bottom end. Hence
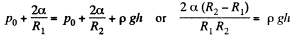
To a first approximation 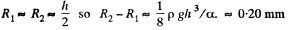
if 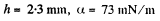
Q. 173. A mercury drop shaped as a round tablet of radius R and thickness h is located between two horizontal glass plates. Assuming that h ≪ R , find the mass m of a weight which has to be placed on the upper plate to diminish the distance between the plates n-times. The contact angle equals θ. Calculate m if R = 2.0 cm, h = 0.38 mm, n = 2.0, and θ = 135°.
Solution. 173. We must first calculate the pressure difference inside the film from that outside. This is
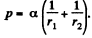
Here 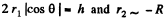 the radius of the tablet and can be neglected. Thus the total force exerted by mercury drop on the upper glass plate i
the radius of the tablet and can be neglected. Thus the total force exerted by mercury drop on the upper glass plate i
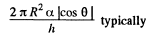
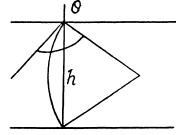
We should put h / n for h because the tablet is com presed n times. Then since Hg is nearly, in com pressible, 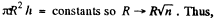
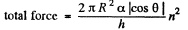
Part of the force is needed to keep the Hg in the shape of a table rather than in the shape of infinitely thin sheet. This part can be calculated being putting n = 1 above. Thus
or 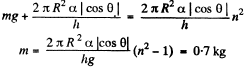
Q. 174. Find the attraction force between two parallel glass plates, separated by a distance h = 0.10 mm, after a water drop of mass m = 70 mg was introduced between them. The wetting is assumed to be complete.
Solution. 174. The pressure inside the film is less than that outside by an amount a 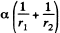 where r1 and r2 are the principal radii of curvature of the meniscus. One of these is small being given by
where r1 and r2 are the principal radii of curvature of the meniscus. One of these is small being given by 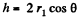 while the other is large and will be ignored. Then
while the other is large and will be ignored. Then 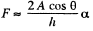 where A = area of the water film between the plates.
where A = area of the water film between the plates.
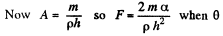 (the angle of contact) = 0
(the angle of contact) = 0
Q. 175. Two glass discs of radius R = 5.0 cm were wetted with water and put together so that the thickness of the water layer between them was h = 1.9 p.m. Assuming the wetting to he complete, find the force that has to be applied at right angles to the plates in order to pull them apart.
Solution. 175. This is analogous to the previous problem except that : A = π R2
So 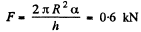
Q. 176. Two vertical parallel glass plates are partially submerged in water. The distance between the plates is d = 0.10 mm, and their width is l = 12 cm. Assuming that the water between the plates does not reach the upper edges of the plates and that the wetting is complete, find the force of their mutual attraction.
Solution. 176. The energy of the liquid between the plates is
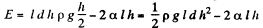
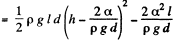
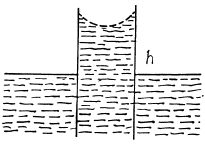
This energy is minimum when, 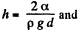 the minimum potential energy is the
the minimum potential energy is the 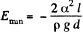
The force of attraction between the plates can be obtained fro m this as
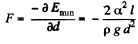 (minus sign means the force is attractive.)
(minus sign means the force is attractive.)
Thus 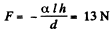
Q. 177. Find the lifetime of a soap bubble of radius R connected with the atmosphere through a capillary of length l and inside radius r. The surface tension is α, the viscosity coefficient of the gas is η.
Solution. 177. Suppose the radius of the bubble is x at some instant. Then the pressure inside is 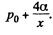 The flow through the capillary is by Poiseuille’s equation,
The flow through the capillary is by Poiseuille’s equation,
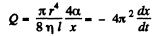
Integrating 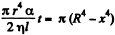 where we have used the fact that t = 0 where x = R.
where we have used the fact that t = 0 where x = R.
This gives 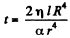 as the life time of the bubble corresponding to x = 0
as the life time of the bubble corresponding to x = 0
Q. 178. A vertical capillary is brought in contact with the water surface. What amount of heat is liberated while the water rises along the capillary? The wetting is assumed to be complete, the surface tension equals α.
Solution. 178. If the liquid rises to a height h', the energy of the liquid column becomes
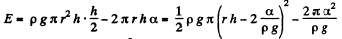
This is minimum when 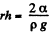 and that is relevant height to which water must rise.
and that is relevant height to which water must rise.
At this point, 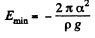
Since E = 0 in the absence o f surface tension a heat 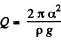 must have been liberated.
must have been liberated.
Q. 179. Find the free energy of the surface layer of
(a) a mercury droplet of diameter d = 1.4 mm;
(b) a soap bubble of diameter d = 6.0 mm if the surface tension of the soap water solution is equal to α = 45 mN/m.
Solution. 179. (a) The free energy per unit area being α,
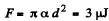
(b) 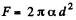 because the soap bubble has two surfaces. Substitution gives
because the soap bubble has two surfaces. Substitution gives 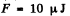
Q. 180. Find the increment of the free energy of the surface layer when two identical mercury droplets, each of diameter d = 1.5 mm, merge isothermally.
Solution. 180. When two mercury drops each of diameter d merge, the resulting drop has diameter d1
where 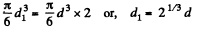
The increase in free energy is
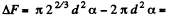
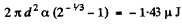
Q. 181. Find the work to be performed in order to blow a soap bubble of radius R if the outside air pressure is equal to p0 and the surface tension of the soap water solution is equal to α.
Solution. 181. Work must be done to stretch the soap film and compress the air inside. The former is simply 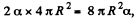 here being two sides o f the film. To get the latter we note that the compression is isothermal and work done is
here being two sides o f the film. To get the latter we note that the compression is isothermal and work done is
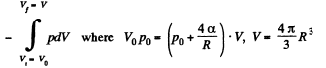
or 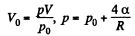
and minus sign is needed becaue we are calculating work done on the system. Thus since pV remains constants, the work done is
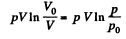
So 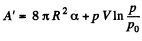
Q. 182. A soap bubble of radius r is inflated with an ideal gas. The atmospheric pressure is p0, the surface tension of the soap water solution is α. Find the difference between the molar heat capacity of the gas during its heating inside the bubble and the molar heat capacity of the gas under constant pressure, C — Cp.
Solution. 182. When heat is given to a soap bubble the temperature of the air inside rises and the bubble expands but unless the bubble bursts, the amount of air inside does not change. Further we shall neglect the variation of the surface tension with temperature. Then from the gas equations
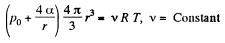
Differentiating
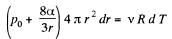
or 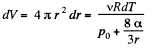
Now from the first law
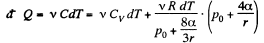
or 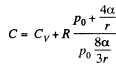
using 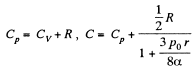
Q. 183. Considering the Carnot cycle as applied to a liquid film, show that in an isothermal process the amount of heat required for the formation of a unit area of the surface layer is equal to q = —T•dα/dT, where dα/dT is the temperature derivative of the surface tension.
Solution. 183. Consider an infinitesimal Carnot cycle with isotherms at T - dT and T. Let A be the work done during the cycle. Then
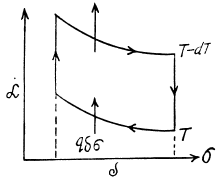
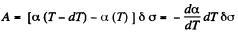
Where δa is the change in the area of film (we are considering only one surface).
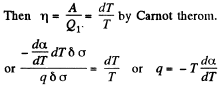
Q. 184. The surface of a soap film was increased isothermally by Δα at a temperature T. Knowing the surface tension of the soap water solution α and the temperature coefficient dα/dT, find the increment
(a) of the entropy of the film's surface layer;
(b) of the internal energy of the surface layer.
Solution. 184. As before we can calculate the heat required. It, is taking into account two sides of the soap film
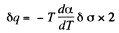
Thus 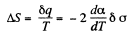
Now 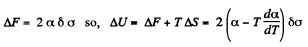
|
95 videos|367 docs|98 tests
|
FAQs on Irodov Solutions: Liquids Capillary Effects - Physics Class 11 - NEET
| 1. What is capillary action? |  |
| 2. How does capillary action work? |  |
| 3. What factors affect capillary action? |  |
| 4. How is capillary action used in everyday life? |  |
| 5. Can capillary action be controlled or manipulated? |  |
















