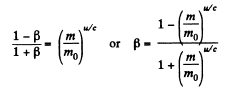Irodov Solutions: Relativistic Mechanics - 3 - Notes | Study Physics Class 11 - NEET

Q.371. Find the velocity at which the relativistic momentum of a particle exceeds its Newtonian momentum η = 2 times. 

Solution. 371. By definition of η,

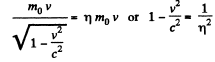
or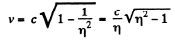 

Q.372. What work has to be performed in order to increase the velocity of a particle of rest mass mo  from 0.60 c to 0.80 c? Compare the result obtained with the value calculated from the classical formula. 

Solution. 372. The work done is equal to change in kinetic energy which is different in the two cases Classically i.e. in nonrelativistic mechanics, the change in kinetic energy is

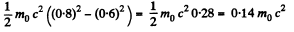
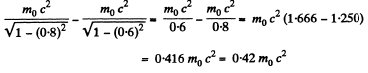
Q.373. Find the velocity at which the kinetic energy of a particle equals its rest energy.

Solution. 373. 

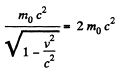
or   

or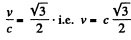   

Q.374.  At what values of the ratio of the kinetic energy to rest energy can the velocity of a particle be calculated from the classical formula with the relative error less than ε = 0.010? 

Solution. 374. Relativistically

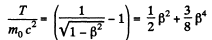
So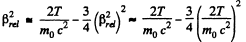   

Thus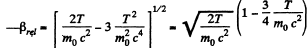   

But Classically,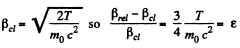   

Hence if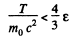  

the velocity β is given by the classical formula with an error less than ε. 

Q.375. Find how the momentum of a particle of rest mass m₀ depends on its kinetic energy. Calculate the momentum of a proton whose kinetic energy equals 500 MeV.

Solution. 375. From the formula

we find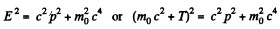 

or   

Q.376. A beam of relativistic particles with kinetic energy T strikes against an absorbing target. The beam current equals I, the charge and rest mass of each particle are equal to e and m₀ respectively. Find the pressure developed by the beam on the target surface, and the power liberated there.

Solution. 376. Let the total force exerted by the beam on the target surface be .F and the power liberated there be P. Then, using the result of the previous problem we see

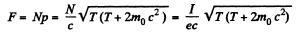
since I = Ne, N being the number of particles striking the target per second. Also,

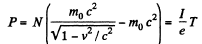
These will be, respectively, equal to the pressure and power developed per unit area of the target if I is current density.

Q.377. A sphere moves with a relativistic velocity v through a gas whose unit volume contains n slowly moving particles, each of mass m. Find the pressure p exerted by the gas on a spherical surface element perpendicular to the velocity of the sphere, provided that the particles scatter elastically. Show that the pressure is the same both in the reference frame fixed to the sphere and in the reference frame fixed to the gas.

Solution. 377. In the tome fixed to the sphere The momentum transferred to the eastically scattered particle is

The density of the moving element is, from 1.369,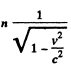 

and the momentum transferred per unit time per unit area is

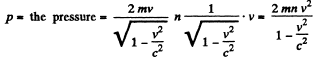
In the frame fixed to the gas When the sphere hits a stationary particle, the latter recoils with a velocity

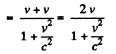
The momentum transferred is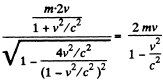  

and the pressure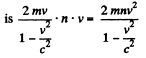  

Q.378. A particle of rest mass mo  starts moving at a moment t = 0 due to a constant force F. Find the time dependence of the particle's velocity and of the distance covered.

Solution. 378. The equation of motion is   

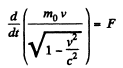
Integrating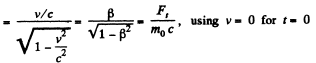  

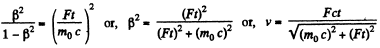
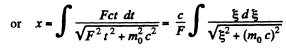
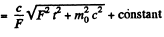
or using r = 0 at r - 0, we get,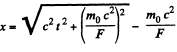 

Q.379. A particle of rest mass m₀ moves along the x axis of the frame K in accordance with the law  where a is a constant, c is the velocity of light, and t is time. Find the force acting on the particle in this reference frame.

Solution. 379.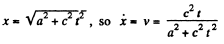   

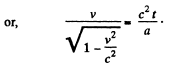
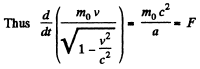
Q.380. Proceeding from the fundamental equation of relativistic dynamics, find:
 (a) under what circumstances the acceleration of a particle coincides in direction with the force F acting on it;
 (b) the proportionality factors relating the force F and the acceleration w in the cases when F ⊥ and F II v, where v is the velocity of the particle.

Solution. 380. 

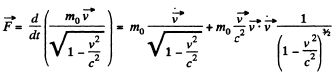
Thus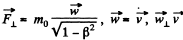  

Q.381. A relativistic particle with momentum p and total energy E moves along the x axis of the frame K. Demonstrate that in the frame K' moving with a constant velocity V relative to the frame K in the positive direction of its axis x the momentum and the total energy of the given particle are defined by the formulas: 

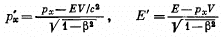
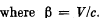
Solution. 381. By definition,

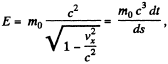
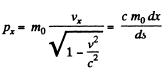
where 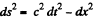  i.s the invariant interval (dy = dz - 0)

Thus,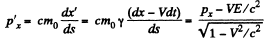 

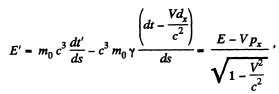
Q.382. The photon energy in the frame K is equal to ε. Making use of the transformation formulas cited in the foregoing problem, find the energy ε' of this photon in the frame K' moving with a velocity V relative to the frame K in the photon's motion direction. At what value of V is the energy of the photon equal to ε' = ε/2?

Solution. 382. For a photon moving in the x direction

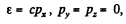
In the moving frame,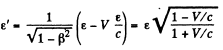 

Note that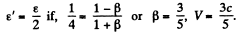 

Q.383. Demonstrate that the quantity E² — p²c²  for a particle is an invariant, i.e. it has the same magnitude in all inertial reference frames. What is the magnitude of this invariant? 

Solution. 383. As before

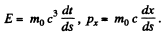
Similarly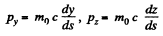 

Then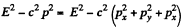 

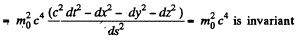
Q.384. A neutron with kinetic energy T = 2m₀c², where m₀ is its rest mass, strikes another, stationary, neutron. Determine: 
 (a) the combined kinetic energy 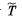of both neutrons in the frame of their centre of inertia and the momentu  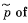each neutron in that frame;
 (b) the velocity of the centre of inertia of this system of particles. Instruction. Make use of the invariant E²  — p²c²  remaining constant on transition from one inertial reference frame to another (E is the total energy of the system, p is its composite momentum).

Solution. 384. (b) & (a) In the CM frame, the total momentum is zero, Thus 

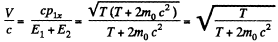
where wc have used the result of problem (Q.375) Then

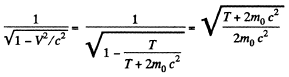
 Total energy in the CM frame is

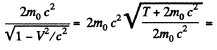
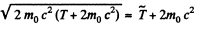
So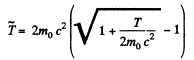   

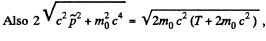
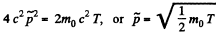
Q.385. A particle of rest mass m₀ with kinetic energy T strikes a stationary particle of the same rest mass. Find the rest mass and the velocity of the compound particle formed as a result of the collision. 

Solution. 385.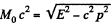 

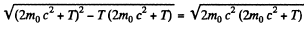
Also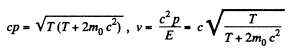  

Q.386. How high must be the kinetic energy of a proton striking another, stationary, proton for their combined kinetic energy in the frame of the centre of inertia to be equal to the total kinetic energy of two protons moving toward each other with individual kinetic energies T = 25.0 GeV? 

Solution. 386. Let T = kinetic energy of a proton striking another stationary particle of the same rest mass. Then, combined kinetic energy in the CM frame

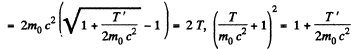
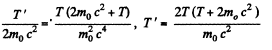
Q.387. A stationary particle of rest mass m₀ disintegrates into three particles with rest masses m₁, m₂, and m₃. Find the maximum total energy that, for example, the particle m₁ may possess. 

Solution. 387. We have

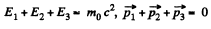
Hence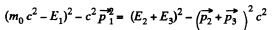 

The L.H.S.  

The R.H.S. is an invariant We can evaluate it in any frame. Choose the CM frame of the particles 2 and 3.

In this frame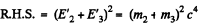  

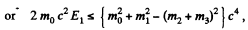
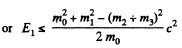
Q.388. A relativistic rocket emits a gas jet with non-relativistic velocity u constant relative to the rocket. Find how the velocity v of the rocket depends on its rest mass m if the initial rest mass of the rocket equals m₀.

Solution. 388. The velocity of ejected gases is u realtive to the rocket. In an earth centred frame it is

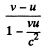
in the direction of the rocket The momentum conservation equation then reads

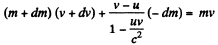
or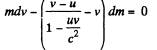 

Here - dm is the mass of the ejected gases, so 

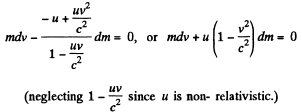
Integrating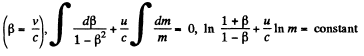  

The constant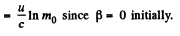  

Thus