Irodov Solutions: Universal Gravitation | Physics Class 11 - NEET PDF Download
Q. 200. A planet of mass M moves along a circle around the Sun with velocity v = 34.9 km/s (relative to the heliocentric reference frame). Find the period of revolution of this planet around the Sun.
Ans. We have
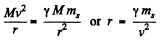
Thus 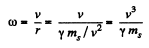
(Here ms the mass of the Sun.)
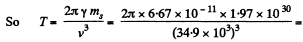
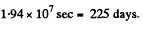
(The answer is incorrectly written in terms of the planetary mass M)
Q. 201. The Jupiter's period of revolution around the Sun is 12 times that of the Earth. Assuming the planetary orbits to be circular, find:
(a) how many times the distance between the Jupiter and the Sun exceeds that between the Earth and the Sun;
(b) the velocity and the acceleration of Jupiter in the heliocentric reference frame.
Ans. For any planet
So, 
(a) Thus 
So 
(b) 
So 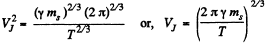
where T = 12 years. ms - mass of ths Sun.
Putting the values we get VJ = 12.97 km/s
Acceleration 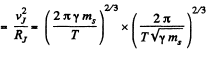
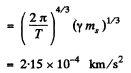
Q. 202. A planet of mass M moves around the Sun along an ellipse so that its minimum distance from the Sun is equal to r and the maximum distance to R. Making use of Kepler's laws, find its period of revolution around the Sun.
Ans. Semi-major axis= (r +/R)/2
It is sufficient to consider the motion be along a circle o f semi-m ajor axis r + R/2 for T does not depend on eccentricity.
Hence 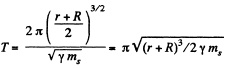
(again ms is the mass of the Sun)
Q. 203. A small body starts falling onto the Sun from a distance equal to the radius of the Earth's orbit. The initial velocity of the body is equal to zero in the heliocentric reference frame. Making use of Kepler's laws, find how long the body will be falling.
Ans. We can think of the body as moving in a very elongated orbit of maximum distance R and minimum distance 0 so semi major axis = R/2. Hence if τ is the time of fall then
or 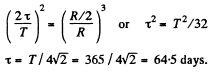
Q. 204. Suppose we have made a model of the Solar system scaled down in the ratio η but of materials of the same mean density as the actual materials of the planets and the Sun. How will the orbital periods of revolution of planetary models change in this case?
Ans. 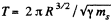
If the distances are scaled down, R3/2 decreases by a factor η3/2 and so does ms . Hence T does not change.
Q. 205. A double star is a system of two stars moving around the centre of inertia of the system due to gravitation. Find the distance between the components of the double star, if its total mass equals M and the period of revolution T.
Ans. The double star can be replaced by a single star of mass 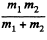 moving about the centre of mass subjected to the force
moving about the centre of mass subjected to the force
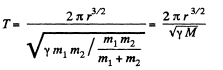
So 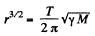
or, 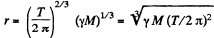
Q. 206. Find the potential energy of the gravitational interaction
(a) of two mass points of masses m1 and m2 located at a distance r from each other;
(b) of a mass point of mass m and a thin uniform rod of mass M and length l, if they are located along a straight line at a distance a from each other; also find the force of their interaction
Ans. (a) The gravitational potential due to m1 at the point of location of m2 :

So, 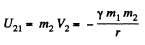
Similarly 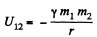
Hence

(b) Choose the location of the point mass as the origin. Then the potential erfeigy dU of an element of mass 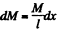 of the rod in the field of the point mass is
of the rod in the field of the point mass is
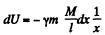
where x is the distance between the element and the point (Note that the rod and the point mass are on a straight line.) If then a is the distance of the nearer end of the rod from the point mass.

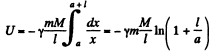
The force of interaction is
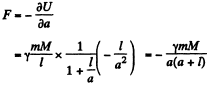
Minus sign means attraction.
Q. 207. A planet of mass m moves along an ellipse around the Sun so that its maximum and minimum distances from the Sun are equal to r1 and r2 respectively. Find the angular momentum M of this planet relative to the centre of the Sun.
Ans. As the planet is under central force (gravitational interaction), its angular momentum is conserved about the Sun (which is situated at one of the focii of the ellipse)
So, 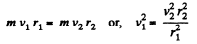 (1)
(1)
From the conservation of mechanical energy of the system (Sun + planet),
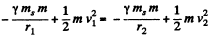
or, 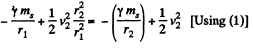
Thus, 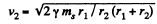 (2)
(2)
Hence 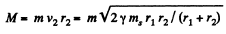
Q. 208. Using the conservation laws, demonstrate that the total mechanical energy of a planet of mass m moving around the Sun along an ellipse depends only on its semi-major axis a. Find this energy as a function of a.
Ans. From the previous problem, if r1 , r2 are the maximum and minimum distances from the sun to the planet and v1 , v2 are the corresponding velocities, then, say,
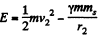
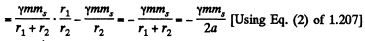
where 2d = major axis = r1 + r2. The same result can also be obtained directly by writing an equation analogous to Eq (1) of problem 1.191.
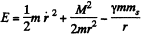
(Here Af is angular momentum of the planet and m is its mass). For extreme position 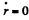 and we get the quadratic
and we get the quadratic
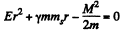
The sum of the two roots of this equation are
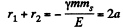
Thus 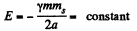
Q. 209. A planet A moves along an elliptical orbit around the Sun. At the moment when it was at the distance r0 from the Sun its velocity 'was equal to v0 and the angle between the radius vector r0 and the velocity vector v0 was equal to α. Find the maximum and minimum distances that will separate this planet from the Sun during its orbital motion.
Ans. From the conservtion of angular momentum about the Sun.
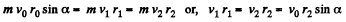 (1)
(1)
From conservation of mechanical eneigy,
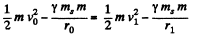
or, 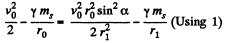
or, 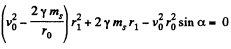
So, 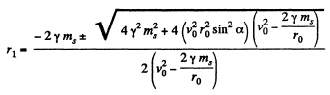
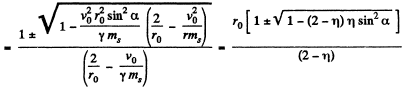
where 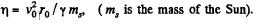
Q. 210. A cosmic body A moves to the Sun with velocity v0(when far from the Sun) and aiming parameter l the arm of the vector v0 elative to the centre of the Sun (Fig. 1.51). Find the minimum distance by which this body will get to the Sun.
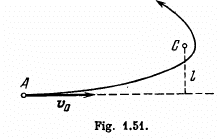
Ans. At the minimum separation with the Sun, the cosmic body’s velocity is perpendicular to its position vector relative to the Sun. If rmin be the sought minimum distance, from conservation of angular momentum about the Sun (C).
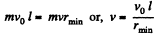 (1)
(1)
From conservation of mechanical energy of the system (sun + cosmic body),
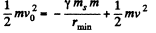
So, 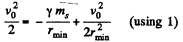
or, 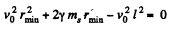
So, 
Hence, taking positive root
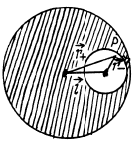
Q. 211. A particle of mass in is located outside a uniform sphere of mass M at a distance r from its centre. Find:
(a) the potential energy of gravitational interaction of the particle and the sphere;
(b) the gravitational force which the sphere exerts on the particle.
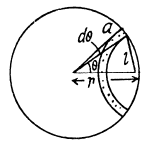
Ans. Suppose that the sphere has a radius equal to a. We may imagine that the sphere is made up of concentric thin spherical shells (layers) with radii ranging from 0 to a, and each spherical layer is made up of elementry bands (rings). Let us first calculate potential due to an elementry band of a spherical layer at the point of location of the point mass m (say point P) (Fig.). As all the points of the band are located at the distance l from the point P, so,
 (1)
(1)
Differentiating Eq. (3), we get
 (4)
(4)
Hence using above equations
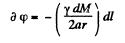 (5)
(5)
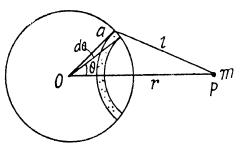
Now integrating this Eq. over the whole spherical layer
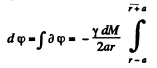
So 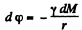 (6)
(6)
Equation (6) demonstrates that the potential produced by a thin uniform spherical layer outside the layer is such as if the whole mass of the layer were concentrated at it’s centre; Hence the potential due to the sphere at point P;
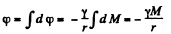 (7)
(7)
This expression is similar to that of Eq. (6)
Hence thte sought potential eneigy of gravitational interaction of the particle m and the sphere,
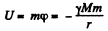
(b) Using the Eq., 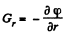
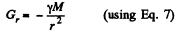
So 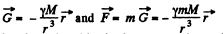 (8)
(8)
Q. 212. Demonstrate that the gravitational force acting on a par- ticle A inside a uniform spherical layer of matter is equal to zero.
Ans. (The problem has already a dear hint in the answer sheet of the problem book). Here we adopt a different method.
Let m be the mass of the spherical layer, wich is imagined to be made up of rings. At a point inside the spherical layer at distance r from the centre, the gravitational potential due to a ring element of radius a equals,
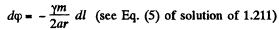
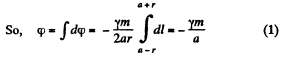
Hence 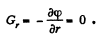
Hence gravitational field strength as well as field force becomes zero, inside a thin sphereical layer.
Q. 213. A particle of mass m was transferred from the centre of the base of a uniform hemisphere of mass M and radius R into infinity. What work was performed in the process by the gravitational force exerted on the particle by the hemisphere?
Ans. One can imagine that the uniform hemisphere is made up of thin hemispherical layers of radii ranging from 0 to R. Let us consider such a layer (Fig.). Potential at point O, due to this layer is,
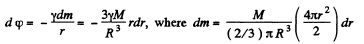
(This is because all points of each hemispherical shell are equidistant from O.)
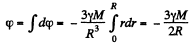
Hence, the work done by the gravitational field force on the particle of mass m, to remove it to infinity is given by the formula
A = mφ , since φ = 0 at infinity.
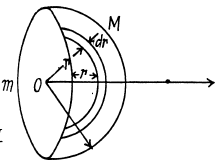
Hence the sought work,
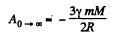
(The work done by the external agent is - A.)
Q. 214. There is a uniform sphere of mass M and radius R. Find the strength G and the potential φ of the gravitational field of this sphere as a function of the distance r from its centre (with r < R and r > R). Draw the approximate plots of the functions G (r) and φ (r).
Ans. In the solution of problem 1.211, we have obtained φ and G due to a uniform shpere, at a distance r from it’s centre outside it We have from Eqs. (7) and (8) of 1.211,
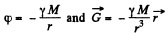 (A)
(A)
Accordance with the Eq. (1) of the solution of 1.212, potential due to a spherical shell of radius a, at any point, inside it becomes
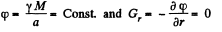 (B)
(B)
For a point (say P) which lies inside the uniform solid sphere, the potential φ at that point may be represented as a sum.
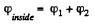
where φ1 is the potential o f a solid sphere having radius r and φ2 is the potential of the layer of radii r and R. In accordance with equation (A)
The potential φ2 produced by the layer (thick shell) is the same at all points inside it. The potential φ2 is easiest to calculate, for the point positioned at the layer’s centre. Using Eq. (B)
where 
is the mass of a thin layer between the radii r and r + dr.
Thus 
From the Eq. 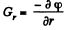
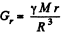
or 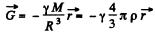
(where 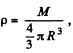 is the density of the sphere) (D)
is the density of the sphere) (D)
The plots φ (r) and G (r) for a uniform sphere of radius R are shown in figure of answersheet.
Alternate : Like Gauss’s theorem of electrostatics, one can derive Gauss’s theorem for gravitation in the form
 at a point inside the sphere at a distance r from its centre, let us consider a Gaussian surface of radius r, Then,
at a point inside the sphere at a distance r from its centre, let us consider a Gaussian surface of radius r, Then,
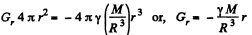
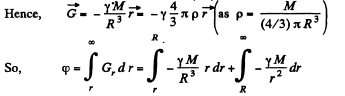
Integrating and summing up, we get
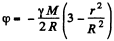
And from Gauss’s theorem for outside it :
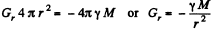
Thus 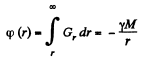
Q. 215. Inside a uniform sphere of density p there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
Ans. Treating the cavity as negative mass of density - p in a uniform sphere density + p and using the superposition principle, the sought field strength is :
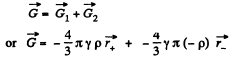
(where 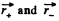 are the position vectors of an orbitrary point P inside the cavity with respect to centre of sphere and cavity respectively.)
are the position vectors of an orbitrary point P inside the cavity with respect to centre of sphere and cavity respectively.)
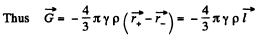
Q. 216. A uniform sphere has a mass M and radius R. Find the pressure p inside the sphere, caused by gravitational compression, as a function of the distance r from its centre. Evaluate p at the centre of the Earth, assuming it to be a uniform sphere.
Ans. We partition the solid sphere into thin spherical layers and consider a layer of thickness dr lying at a distance r from the centre of the ball. Each spherical layer presses on the layers within it The considered layer is attracted to the part of the sphere lying within it (the outer part does not act on the layer). Hence for the considered layer
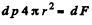

(The pressure.must vanish at r = R.)
or, 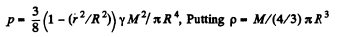
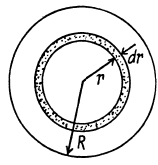
Putting r = 0, we have the pressure at sphere’s centre, and treating it as the Earth wheremean density is equal to 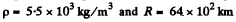
we have , 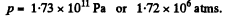
Q. 217. Find the proper potential energy of gravitational interaction of matter forming
(a) a thin uniform spherical layer of mass m and radius R;
(b) a uniform sphere of mass m and radius R (make use of the answer to Problem 1.214).
Ans. (a) Since the potential at each point of a spherical surface (shell) is constant and is equal to 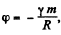 [as we have in Eq. (1) of solution of problem 1.212]
[as we have in Eq. (1) of solution of problem 1.212]
We obtain in accordance with the equation
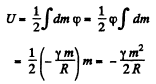
(The factor 1/2 is needed otherwise contribution of different mass elements is counted twice.]
(b) In this case the potential inside the sphete depends only on r (see Eq. (C) of the solution of oroblem 1.214)
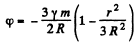
Here dm is the mass of an elementry spherical layer confined between the radii r and r + dr :
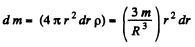
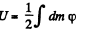
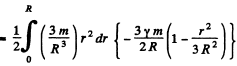
After integrating, we get

Q. 218. Two Earth's satellites move in a common plane along circular orbits. The orbital radius of one satellite r = 7000 km while that of the other satellite is Δr = 70 km less. What time interval separates the periodic approaches of the satellites to each other over the minimum distance?
Ans. 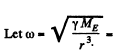 circular frequency o f the satellite in the outer orbit,
circular frequency o f the satellite in the outer orbit,
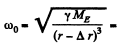 ircular frequency of the satellite in the inner orbit
ircular frequency of the satellite in the inner orbit
So, relative angular velocity 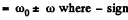 is to be taken when the satellites are moving in the same sense and + sign if they are moving in opposite sense.
is to be taken when the satellites are moving in the same sense and + sign if they are moving in opposite sense.
Hence, time between closest approaches
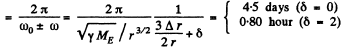
where δ is 0 in the first case and 2 in the second case.
Q. 219. Calculate the ratios of the following accelerations: the acceleration w1 due to the gravitational force on the Earth's surface, the acceleration w2 due to the centrifugal force of inertia on the Earth's equator, and the acceleration w3 caused by the Sun to the bodies on the Earth.
Ans. 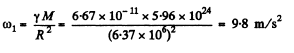
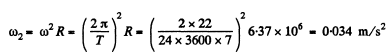
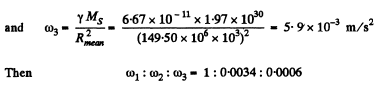
Q. 220. At what height over the Earth's pole the free-fall acceleration decreases by one per cent; by half?
Ans. Let h be the sought height in the first case, so
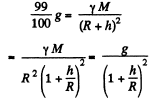
or 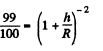
From the statement of the problem, it is obvious that in this case h<<R
Thus 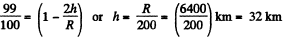
In the other case if h! be the sought height, than
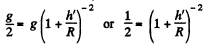
From the language o f the problem, in this case h' is not very small in comparison with R. Therefore in this case we cannot use the approximation adopted in the previous case.
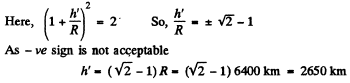
Q. 221. On the pole of the Earth a body is imparted velocity v0 directed vertically up. Knowing the radius of the Earth and the freefall acceleration on its surface, find the height to which the body will ascend. The air drag is to be neglected.
Ans. Let the mass of the body be m and let it go upto a height h.
From conservation of mechanical energy of the system
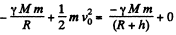
Using 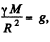 in above equation and on solving we get,
in above equation and on solving we get,
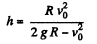
Q. 222. An artificial satellite is launched into a circular orbit around the Earth with velocity v relative to the reference frame moving translationally and fixed to the Earth's rotation axis. Find the distance from the satellite to the Earth's surface. The radius of the Earth and the free-fall acceleration on its surface are supposed to be known.
Ans. Gravitational pull provides the required centripetal acceleration to the satelite. Thus if h be the sought distance, we have
so, 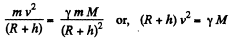
or, 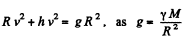
Hence 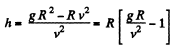
Q. 223. Calculate the radius of the circular orbit of a stationary Earth's satellite, which remains motionless with respect to its surface. What are its velocity and acceleration in the inertial reference frame fixed at a given moment to the centre of the Earth?
Ans. A satellite that hovers above the earth’s equator and corotates with it moving from the west to east with the diurnal angular velocity of the earth appears stationary to an observer on the earth. It is called geostationary. For this calculation we may neglect the annual motion of the earth as well as all other influences. Then, by Newton’s law,
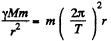
where M = mass of the earth, T = 86400 seconds = period of daily rotation of the earth and r = distance of the satellite from the centre of the earth. Then
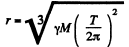
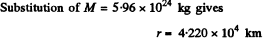
The instantaneous velocity with respect to an inertial frame fixed to the centre of the earth at that moment will be
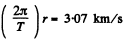
and the acceleration will be the centripetal acceleration.

Q. 224. A satellite revolving in a circular equatorial orbit of radius R = 2.00-104 km from west to east appears over a certain point at the equator every τ = 11.6 hours. Using these data, calculate the mass of the Earth. The gravitational constant is supposed to be known.
Ans. We know from the previous problem that a satellite moving west to east at a distance R = 2-00 x 104 km from the centre of the earth will be revolving round the earth with an angular velocity faster than the earth’s diurnal angualr velocity. Let
ω = angular velocity of the satellite
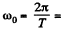 anuglar velocity of the earth. Then
anuglar velocity of the earth. Then
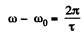
as the relative angular velocity with respect to earth. Now by Newton’s law
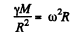
So, 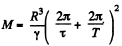
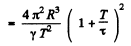
Substitution gives
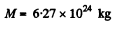
Q. 225. A satellite revolves from east to west in a circular equatorial orbit of radius R = 1.00.104 km around the Earth. Find the velocity and the acceleration of the satellite in the reference frame fixed to the Earth.
Ans. The velocity of the satellite in the inertial space fixed frame is 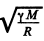 east to west . With respect to the Earth fixed frame, from the
east to west . With respect to the Earth fixed frame, from the 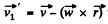 the velocity is
the velocity is
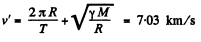
Here M is the mass of the earth and T is its period of rotation about its own axis.
It would be 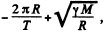 if the satellite were moving from west to east
if the satellite were moving from west to east
To find the acceleration we note the formula
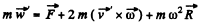
Here 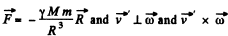 is directed towards the centre of the Earth.
is directed towards the centre of the Earth.
Thus 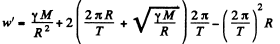
toward the earth’s rotation axis
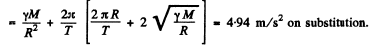
Q. 226. A satellite must move in the equatorial plane of the Earth close to its surface either in the Earth's rotation direction or against it. Find how many times the kinetic energy of the satellite in the latter case exceeds that in the former case (in the reference frame fixed to the Earth).
Ans. From the well known relationship between the velocities of a particle w.r.t a space fixed fram e (K) rotating frame 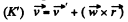
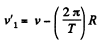
Thus kinetic energy of the satellite in the earth’s frame
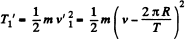
Obviously when the satellite moves in opposite sense comared to the rotation of the Earth its velocity relative to the same frame would be
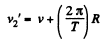
And kinetic energy
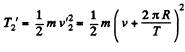 (2)
(2)
From (1) and (2)
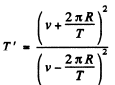 (3)
(3)
Now from Newton’s second law
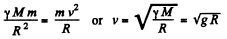 (4)
(4)
Using (4) and (3).
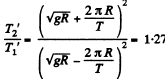 nearly (Using Appendices)
nearly (Using Appendices)
Q. 227. An artificial satellite of the Moon revolves in a circular orbit whose radius exceeds the radius of the Moon η times. In the process of motion the satellite experiences a slight resistance due to cosmic dust. Assuming the resistance force to depend on the velocity of the satellite as F = αv2, where a is α constant, find how long the satellite will stay in orbit until it falls onto the Moon's surface.
Ans. For a satellite in a circular orbit about any massive body, the following relation holds between kinetic, potential & total eneigy :
 (1)
(1)
Thus since total mechanical energy must decrease due to resistance of the cosmic dust, the kintetic energy will increase and the satellite will 'fair, We see then, by work eneigy theorm
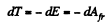
So, 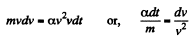
Now from Netow’s law at an arbitray radius r from the moon’s centre.
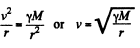
(M is the mass of the moon.) Then

where R= moon’s radius. So
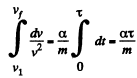
or, 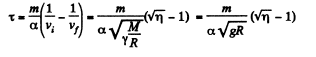
where g is moon’s gravity. The averaging implied by Eq. (1) (for noncircular orbits) makes the result approximate.
Q. 228. Calculate the orbital and escape velocities for the Moon. Compare the results obtained with the corresponding velocities for the Earth.
Ans. From Newton’s second law
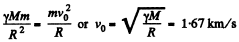 (1)
(1)
From conservation of mechanical energy
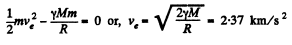 (2)
(2)
In Eq. (1) and (2), M and R are the mass of the moon and its radius. In Eq. (1) if M and R represent the mass of the earth and its radius, then, using appendices, we can easily get

Q. 229. A spaceship approaches the Moon along a parabolic trajectory which is almost tangent to the Moon's surface. At the moment of the maximum approach the brake rocket was fired for a short time interval, and the spaceship was transferred into a circular orbit of a Moon satellite. Find how the spaceship velocity modulus increased in the process of braking.
Ans. In a parabolic orbit, E = 0
So 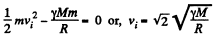
where M = mass of the Moon, R = its radius. (This is just the escape velocity.) On the other hand in orbit
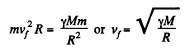
Thus 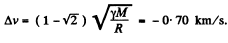
Q. 230. A spaceship is launched into a circular orbit close to the Earth's surface. What additional velocity has to be imparted to the spaceship to overcome the gravitational pull?
Ans. From 1.228 for the Earth surface
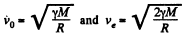
Thus the sought additional velocity

This ‘kick’ in velocity must be given along the direction of motion of the satellite in its orbit
Q. 231. At what distance from the centre of the Moon is the point at which the strength of the resultant of the Earth's and Moon's gravitational fields is equal to zero? The Earth's mass is assumed to be η = 81 times that of the Moon, and the distance between the centres of these planets n = 60 times greater than the radius of the Earth R.
Ans. Let r be the sought distance, then
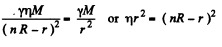
or 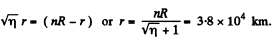
Q. 232. What is the minimum work that has to be performed to bring a spaceship of mass m = 2.0.103 k g from the surface of the Earth to the Moon?
Ans. Between the earth and the moon, the potential energy of the spaceship will have a maximum at the point where the attractions of the earth and the moon balance each other. This maximum RE. is approximately zero. We can also neglect the contribution of either body to the p.E. of the spaceship sufficiently near the other body. Then the minimum energy that must be imparted to the spaceship to cross the maximum of the P.E. is clearly (using E to denote the earth)
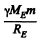
With this energy the spaceship will cross over the hump in the P.E. and coast down the hill of p.E. towards the moon and crashland on it. What the problem seeks is the minimum energy reguired for softlanding. That reguies the use of rockets to loving about the braking of the spaceship and since the kinetic energy of the gases ejected from the rocket will always be positive, the total energy required for softlanding is greater than that required for crashlanding. To calculate this energy we assume that the rockets are used fairly close to the moon when the spaceship has nealy attained its terminal velocity on the moon 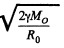 where M0 is the mass of the moon and R0 is its radius. In general dE = vdp and since the speed of the ejected gases is not less than the speed of the rocket, and momentum transfered to the ejected gases must equal the momentum of the spaceship the energy E of the gass ejected is not less than the kinetic energy of spaceship
where M0 is the mass of the moon and R0 is its radius. In general dE = vdp and since the speed of the ejected gases is not less than the speed of the rocket, and momentum transfered to the ejected gases must equal the momentum of the spaceship the energy E of the gass ejected is not less than the kinetic energy of spaceship
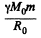
Addding the two we get the minimum work done on the ejected gases to bring about the softlanding.
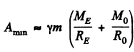
On substitution we get 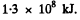
Q. 233. Find approximately the third cosmic velocity v3, i.e. the minimum velocity that has to be imparted to a body relative to the Earth's surface to drive it out of the Solar system. The rotation of the Earth about its own axis is to be neglected.
Ans. Assume first that the attraction of the earth can be neglected. Then the minimum velocity, that must be imparted to the body to escape from the Sun’s pull, is, as in 1*230, equal to 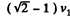
where 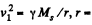 radius of the earth’s orbit, Ms - mass of the Sun.
radius of the earth’s orbit, Ms - mass of the Sun.
In the actual case near the earth, the pull of the Sun is small and does not change much over distances, which are several times the radius of the Earth. The velocity v3 in question is that which overcomes the earth’s pull with sufficient velocity to escape the Sun’s pull.
Thus
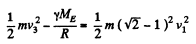
where R = radius of the earth, ME = mass of the earth.
Writing 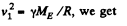
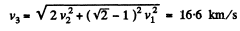
|
96 videos|367 docs|98 tests
|
FAQs on Irodov Solutions: Universal Gravitation - Physics Class 11 - NEET
| 1. What is universal gravitation according to Irodov Solutions? |  |
| 2. How is universal gravitation related to the JEE exam syllabus? |  |
| 3. What are some common problems related to universal gravitation that students may encounter in the JEE exam? |  |
| 4. How can students effectively prepare for questions on universal gravitation in the JEE exam? |  |
| 5. Are there any specific tips or strategies for mastering universal gravitation concepts for the JEE exam? |  |

















