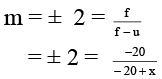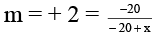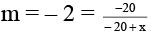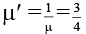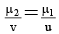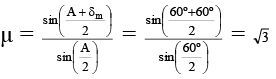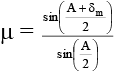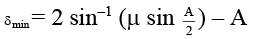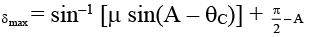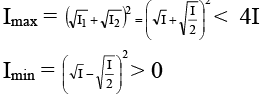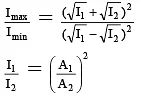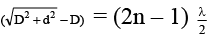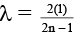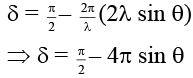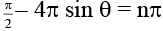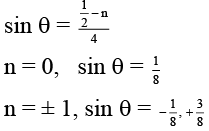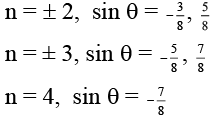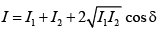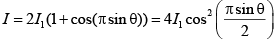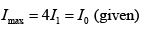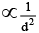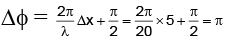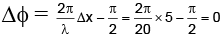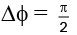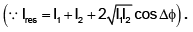JEE Advanced (One or More Correct Option): Ray & Wave Optics | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. A plane mirror having a square shape is mounted parallel to a vertical wall at some distance from it. A point light source is fixed on the wall. Light from it gets reflected from the mirror and forms a patch on the wall, when the mirror is moved parallel to itself towards the wall –
(a) centre of patch may remain stationary
(b) the patch may remain square in shape
(c) area of patch decreases
(d) none of the above

Correct Answer is options (a, b, c)
If the mirror is moved parallel to itself with velocity along the line, normal to wall and passing through the source, then patch will remain unchanged in shape and size.

Q.2. The image of a real object formed by a concave mirror is twice the size of the object. The focal length of the mirror is 20 cm. The distance of the object from the mirror -
(a) 10 cm
(b) 30 cm
(c) 25 cm
(d) 15 cm

Correct Answer is Options (a, b)

If
– 40 + 2x = – 20
2x = 20
x = 10 cm
if
40 – 2x = – 20
x = 30

Q.3. Which of the following statements are correct?
(a) Real image of a real object cannot be formed by a plane mirror.
(b) Real image of a real object cannot be formed by a convex mirror.
(c) Real image of a real object cannot be formed by a concave lens.
(d) None of the above.

Correct Answer is options (a, b, c)
If a real object is placed in front of a plane mirror, then its image will be formed behind the mirror. Since, the image formed behind the mirror is always virtual, therefore, a real image of a real object cannot be formed by a plane mirror. Hence, option (A) is correct. Convex mirror is a diverging mirror. If a real object is placed in front of a convex mirror then rays coming from the object will be diverging. It means, diverging light rays will be incident on a diverging mirror which will further diverge these rays. Hence, the reflected rays will also be diverging. Therefore, the image will be formed behind the mirror. Hence, the image will be virtual. Therefore, option (B) is correct.
A concave lens is a diverging lens. If a real object is placed on its optic axis then light rays coming from the object on the lens will be diverging which will be further diverged by the lens after refraction. Hence, the reflected light rays will be diverging. The position of image will be the point of divergence of refracted rays. It means, the image will be virtual. Hence, option (C) is also correct.

Q.4. In passing through a boundary refraction will not take place if –
(a) light is incident normally on the boundary.
(b) the indices of refraction of the two media are same.
(c) the boundary is not visible if µ₁ = µ₂.
(d) angle of incidence is lesser than the angle of refraction but greater than sin–1 (µ_R/µ_D).

Correct Answer is options (c, d)
When light is incident normally on the boundary, then i = 0. So, according to Snell's law µ₁ sin i = µ₂ sin r, r is also zero, i.e., there is not refraction.
If µ₁ = µ₂, then boundary will not be visible and r = i, i.e., there will be no refraction. If i < r and i > sin^–1 (µ_R/µ_D) or i > i_c (critical angle), then also there will be no refraction of light and light will be totally internally reflected.

Q.5. A fish F, in the pond is at a depth of 0.8 m from the water surface and is moving vertically upwards with velocity 2 ms^–1. At the same instant a bird B is at a height of 6 m from the water surface and is moving downwards with velocity 3 ms^–1. At this instant both are on the same vertical line as shown in the figure. Which of the following statements are correct?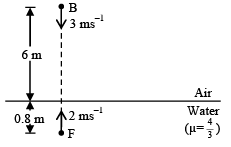
(a) Height of B, observed by F (from itself) is equal to 5.30 m
(b) Depth of F, observed by B (from itself) is equal to 6.60 m
(c) Height of B, observed by F (from itself) is equal to 8.80 m
(d) None of the above

Correct Answer is options (b, c)
If an object is at a distance x from a plane refracting surface and is viewed normally then it appears at a distance x/µ from the surface where µ is refractive index of that medium (in which it is situated) with respect to the medium in which observer is situated.
Suppose height of bird from water surface is x and depth of fish from the surface is y then depth of fish, observed by the bird, will be equal to

Where µ is refractive index of water with respect to air.
∴ r₁ = 6.60 m
Hence, option (B) is correct.
Height of bird, observed by fish, will be equal to

Where µ' is refractive index of air with respect to water.
Now,
Hence, r₂ = 8.80 m
Hence, option (a) is wrong while (c) is correct.

Q.6. A bird flies down vertically towards a water surface. To a fish inside the water, vertically below the bird, the bird will appear to –
(a) be farther away than its actual distance
(b) be closer than its actual distance
(c) move faster than its actual speed
(d) move slower than its actual speed

Correct Answer is options (a, c)
For refraction at plane surface,

Let x = height of the bird above the water surface For light travelling from the bird to fish,
µ₁ = 1, µ₂ = µ (refractive index of water) and u = –x,
hence,  or v = – µx
or, | v | = µx, i.e., | v | > x
Speed of the bird = x
∴ Apparent speed of the bird = | v | = µx

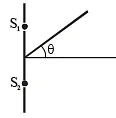
Q.7. The angle of deviation (δ) vs angle of incidence (i) is plotted for a prism. Pick up the correct statements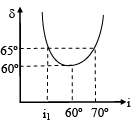
(a) The angle of prism is 60º
(b) the refractive index of the prism is n = 3
(c) For deviation to be 65º the angle of incidence i1 = 55º
(d) The curve of 'd' vs 'i' is parabolic.

Correct Answer is options (a, b, c)
δ = i  + e – A (for minimum deviation i = e)
∴ minimum deviation = 2i – A
60º = 2 × 60º – A ⇒ ΘA = 60º

δ₁ = i₁ + e - A
65º = i₁ + 70º -  60 º or i₁ = 55º
The d versus i curve is not parabolic.

Q.8. Refractive index of an equilateral prism is √2 -
(a) minimum deviation from this prism can be 30º
(b) minimum deviation from this prism can be 45º
(c) at angle of incidence = 45º, deviation is minimum
(d) at angle of incidence = 60º, deviation is minimum

Correct Answer is options (a, c)

δm = 30º for μ = √2 & A = 60º
At minimum deviation
r₁ = r₂ = A/2 = 30º
sin i₁ = μ sin r₁
= √2 sin (30º)
= 1/√2
⇒ i₁ = 45º

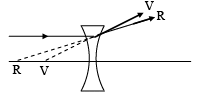
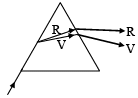
Q.9. Which of the following quantities increases when wavelength is increased. Consider only the magnitudes -
(a) The focal length of a converging lens.
(b) The focal length of a diverging lens.
(c) The angle of minimum deviation caused by a prism.
(d) The angle of maximum deviation caused by a prism, without total internal reflection.

Correct Answer is options (a, b)
μ_V > μ_R λ_R > λ_V
(A)

(B)
 
(C)
 
(D)

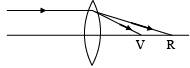
Q.10. A short linear object is placed along the optic axis of a concave mirror between focus and curvature centre, then –
(a) a real elongated image will be formed.
(b) an elongated virtual image will be formed.
(c) an inverted, enlarged image will be formed.
(d) a diminished virtual image will be formed.

Correct Answer is options (a, c)
If an object is placed between focus and curvature centre of a concave mirror, then a real, elongated image is formed. Hence, option (a) is correct.
Since, real image is always inverted; therefore, option (c) is also correct.

Q.11. If one of the slits of a standard young‘s double slit experiment is covered by a thin parallel slit glass so that it transmits only one half the light intensity of the other, then:
(a) The fringe pattern will get shifted towards the covered slit
(b) The fringe pattern will get shifted away from the covered slit
(c) The bright fringes will become less bright and the dark ones will become brighter
(d) The fringe width will remain unchanged

Correct Answer is options (a, c, d)
I₁ = I₂ = I

Q.12. In the Young’s double slit experiment, the interference pattern is found to have an intensity ratio between bright and dark fringes as 9. This implies that -
(a) the intensities at the screen due to the two slits are 5 units and 4 units respectively
(b) the intensities at the screen due to the two slits can be 4 units and 1 unit respectively
(c) the amplitude ratio is 3
(d) the amplitude ratio is 2

Correct Answer is options (b, d)

we can find I₁ / I₂ from equation (1) and A₁ / A₂ from equation (2)

Q.13. If the first minima in a young's slit experiment occurs directly in front of one of the slits, (distance between slits and screen d = 5cm) then the wavelength of the radiation used can be:
(a) 2 cm
(b) 4 cm
(c) 3/2 cm
(d) 3/4 cm 

Correct Answer is options (a, c)
Path difference =  = 1 cm
Also,
⇒
l = 2cm, 2/3 cm, 2/5 cm
Hence (a, c)

Q.14. In a modified YDSE experiment if point source of monochromatic light O is placed in such a manner that OS₁– OS₂ = λ/4 where l is wavelength of light and S₁, S₂ are slits separated by distance 2λ. Then value/s of θ for which a maxima is obtained will be -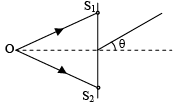
(a) sin^–1 (1/8)
(b) sin^–1 (–1/4)
(c) sin^–1 (5/6)
(d) sin^–1 (–7/8)  

Correct Answer is options (a, d)

For maxima, δ = nπ
where n = 0, ± 1, ± 2 . . .

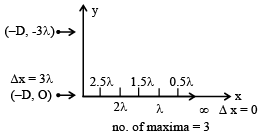
Q.15. Two coherent sources A & B emitting light of wavelength λ are placed at positions (-D, O) and (-D, 3λ) respectively D >>> λ -
(a) number of minima on y axis is 6.
(b) number of minima is more than number of maxima on y axis.
(c) number of maxima on x axis is 3.
(d) number of maxima on x axis is more than number of minima on x axis.

Correct Answer is options (a, b, c)
Δx at ∞ on y axis is 3λ & - 3λ. there will be 6 minima & 5 maxima

Q.16. In an interference experiment similar to Young’s double slit experiment, the slits S₁ and S₂ are illuminated with coherent microwave sources, each of frequency 10⁶ Hz. The source are synchronised to have zero phase difference. The slits are separated by a distance d = 150.0 m. The intensity I (θ) is measured as a function of θ , where q is defined as shown. O is the centre of two slits. If Iθ is the maximum intensity, then I (θ) for 0 ≤ θ ≤ 90° is given by

(a) I(θ) = I₀ / 2 for θ = 30°
(b) I(θ) = I₀ / 4 for θ = 90°
(c) I(θ) = I₀ for θ = 0°
(d) I(θ) is constant for all values of θ

Correct Answer is options (a, c)
For microwaves  = 300 m.
Path difference δ = d sin θ
∴ Phase difference
Intensity

I will be maximum when  is maximum = 1.

So,
i.e, (a) and (c) are correct.

Q.17. Coherent light consisting of two wavelengths λ₁ = 4500 Å & λ₂ = 6000 Å is sent through both slits of a Young's double slit apparatus
(a) Central maxima for both wavelengths will coincide
(b) The third order bright fringe of λ₁ will coincide with the fourth order bright fringe of λ₂
(c)  The third order bright fringe of λ₂ will coincide with fourth order bright fringe  of λ₁
(d) The fringes of wavelength λ₁ will be wider than the fringes of wavelength λ₂

Correct Answer is options (a, c)
 for central maxima ΔX = 0, hence y = 0. (Does not depend upon λ)
 n × 4500 = m × 6000
3n = 4m. n = 4,   m = 3.

Q.18. When a monochromatic point source of light is at a distance of 1 m from a photoelectric cell, the cut-off voltage and the saturation current are respectively 0.4 V and 36 mA. If the same source is placed 2 m away from the photoelectric cell, then –
(a) The stopping potential will be 0.4 V
(b) The stopping potential will be 0.2 V
(c) The saturation current will be 18 mA
(d) The saturation current will be 9 mA

Correct Answer is options (a, d)
Number of photons received/area
∴ Saturation current becomes 1/4^th
Stopping potential depends on frequency which is unchanged.

Q.19. Which of the following statement about X-rays is/are true?
(a) E(k_α) + E(L_β) = E(k_β ) + E(M_α) = E(k_γ), where E is the energy of respective X-rays.
(b) For the harder X-rays, the intensity is higher than soft X-rays.
(c) The continuous and the characteristic X-rays differ only in the method of creation.
(d) The cut-off wavelength λ_min depends only on the accelerating voltage applied between the target and the filament.

Correct Answer is options (a, c, d)
E(k_α) + E(L_β) = E(k_β ) + E(M_α) = E(k_γ)
Harder X – rays have higher frequency than the softer X-ray. Continuous and characteristic X-rays differ only in the method of creation.

Q.20. Two monochromatic sources of electromagentic wave, P and Q emit waves of wavelength λ = 20 m and separated by 5m as shown. A, B and C are three points where interference of these waves occurs. If phase of a wave generated by P is ahead of wave generated by Q by π/2 then (given intensity of both waves is I) :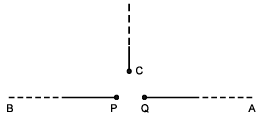
(a) phase difference of these waves at B is 180°
(b) intensities at A, B and C are in the ratio 2 : 0 : 1 respectively.
(c) intensities at A, B and C are in the ratio 1 : 2 : 0 respectively.
(d) phase difference at A is 0°.

Correct Answer is options (a, b)
(A) At B,
(B) At A,
At C,
∴ I_A : I_B : I_C = 4I : 0 : 2I = 2 : 0 : 1