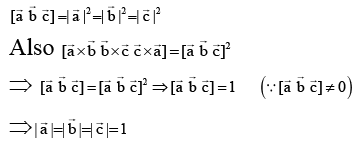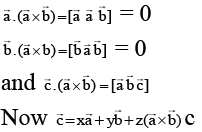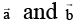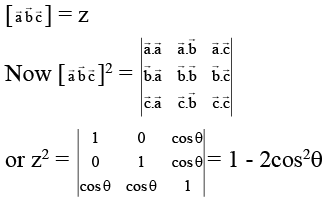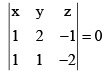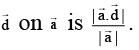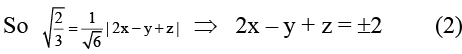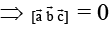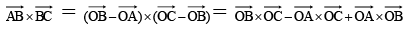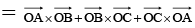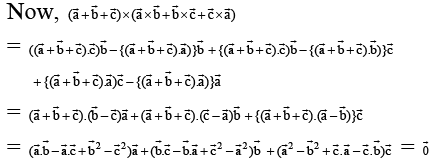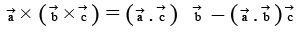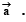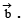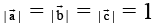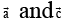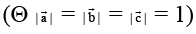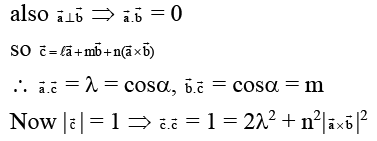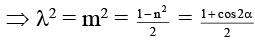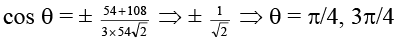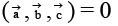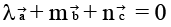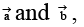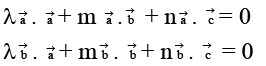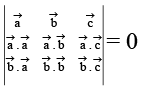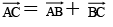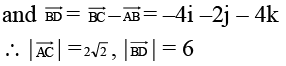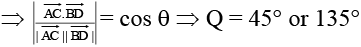JEE Advanced (One or More Correct Option): Vector Algebra | Chapter-wise Tests for JEE Main & Advanced PDF Download

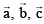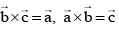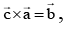Q.1. If   are non-coplanar vectors such that  and  then
(a)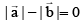
(b)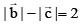
(c)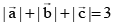
(d)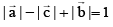

Correct Answer is option (a, c, d)

Q.2. 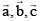 are unit vector such that  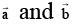mutually perpendicular and  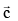is equally inclined to  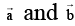at an angle θ. If  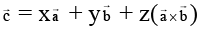then 
(a) z² = 1 - 2y²
(b) z² = 1 - x² - y² 
(c) z² = 1 - 2x² 
(d) x² = y²

Correct Answer is option (a, b, c, d)

Hence a, b, c, d.]

Multiplying both sides scalarly by
cos θ = x .1 + 0 + 0 = x ,  cosq = y.1 = y  
 = x.0 + y.0 + z(a × (b)² = z.1 = z [a b c] = z

∴ z² = 1 - 2x² = 1 - 2y²
Also, x² = y² 

Q.3. Let 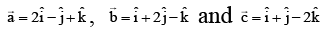 be three vectors. A vector in the plane of  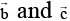whose projection on  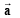is of magnitude √2/3 is
(a)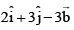  
(b)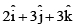
(c)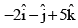
(d)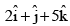

Correct Answer is option (a, c)
Let the required vector be  For this to be coplanar with  we must have

⇒ x(-4 + 1) + y(-1 + 2) + z(1 - 2) = 0
⇒ -3x + y - z = 0         ....(1)
The projection of


The choices (a) and (c) satisfy the equations (1) and (2).

Q.4. Which of the following statements is/are correct?
(a) If 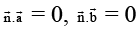 and 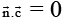 for some non-zero vectors  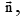then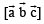

= 0

(b) There exist a vector making angles 30º and 45º with x and y axes respectively.
(c) Locus of point for which x = 3 and y = 4 is a line parallel to the z-axis whose distance from the z-axis, is 5.
(d) The vertices of a regular tetrahedron are O, A, B, C where 'O' is the origin.  The vector 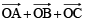 is perpendicular the plane ABC.

Correct Answer is option (a, c, d)
(a) since 
 are coplanar

(b) cos²30º + cos²45º + cos²γ = 1
∴ sin²g =  which is not possible.
(c) Obvious
(d)

i.e.,  is perpendicular to the plane ABC.

Hence, the statement is true.

Q.5. If 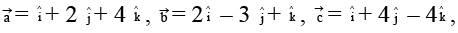 then the vector  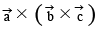is orthogonal to -
(a)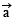
(b)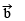
(c)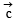
(d)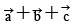

Correct Answer is option (a, d)

and this is orthogonal to
 is also orthogonal to

Q.6. Let the unit vector 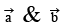 are perpendicular and the moduli vector  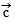inclined at an angle α to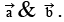

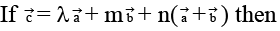
(a) λ = m
(b) n² = 1 – 2λ²
(c) n² = - cos 2α
(d)

Correct Answer is option (a, b, c, d)

angle between  = angle between
 

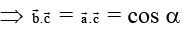
⇒ m = λ= cos α
⇒ 1 = 2λ² + n² ⇒ n² = 1 - 2λ² = 1 - 2cos²α
= - cos²α

Hence, all are correct.

Q.7. Let A be vector parallel to the line of intersection of planes P₁ and P₂ through origin. P₁ is parallel to the vectors 2j + 3k and 4j – 3k and P₂ is parallel to j – k and 3i + 3j, then the angle between A and 2i + j – 2k is -
(a) π/2
(b) π/4
(c) p/6
(d) 3p/4

Correct Answer is option (b, d)
vector  is parallel to
[(2j + 3k) × (4j – 3k)] × [(j – k) × (3i + 3j)] ⇒ 54 (j – k)
If θ is the required angle then  

Q.8. If the vectors 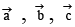 are coplanar, then -
(a)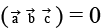
(b)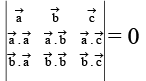
(c)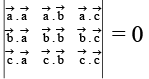
(d) None of these

Correct Answer is option (a, b, c)
 are coplanar and hence
Also scalars exist such that
Taking the dot product with

Eliminating l, m, n, we have
Taking dot product with  and eliminating λ, m, n we get the other determinant equal to zero.

Q.9. The vectors 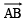 = 3i + 2j + 2k &  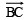= –i – 2k are adjacent sides of a parallelogram then angle between diagonals is
(a) 60°
(b) 45°
(c) 90°
(d) 135°

Correct Answer is option (b, d)
Θ The diagonals

= 2i + 2j

∴ Angle between diagonals is

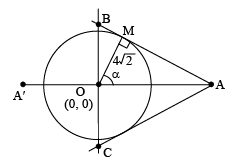
Q.10. Tangents are drawn to circle x² + y² = 32 from a point A lying on x-axis. The tangent cut y- axis at point B & C then coordinates of A such that area of DABC is minimum may be
(a) (8, 0)
(b) (6, 0)
(c) (–8, 0)
(d) (–6, 0)

Correct Answer is option (a, b)
OM = 4√2

OA = 4√2 sec a
BC = 2OB = 8√2 cosec α
∴  Area of
For min. area a = π/4
∴  Point A is (8, 0) symmetrically A'(-8, 0)