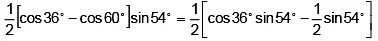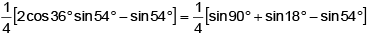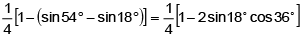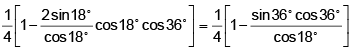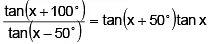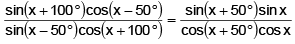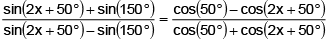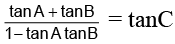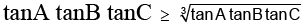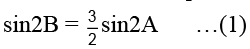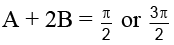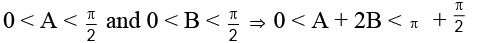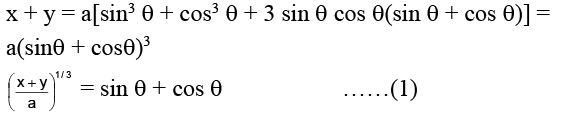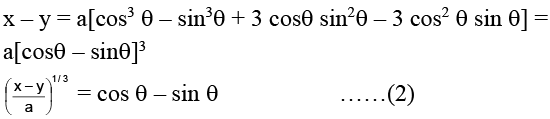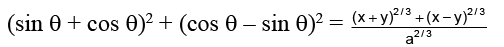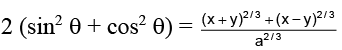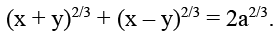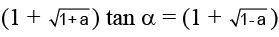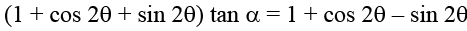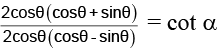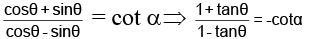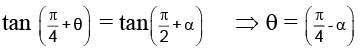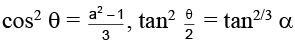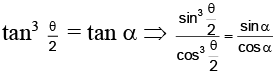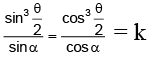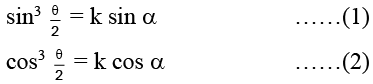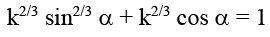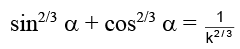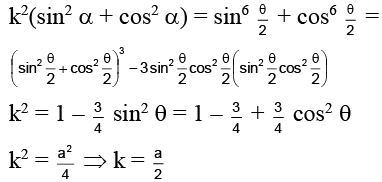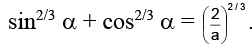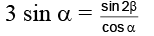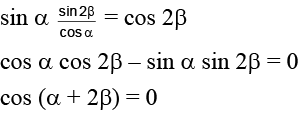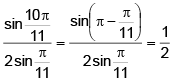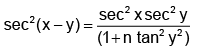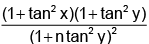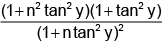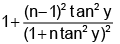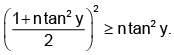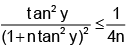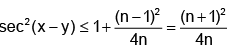JEE Advanced (Single Correct Type): Trigonometric Equations & Functions | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. If sin θ and cos θ are the roots of ax² – bx + c = 0, then the relation between a, b and c will be
(a) a² + b² + 2ac = 0
(b) a² – b² + 2ac = 0
(c) a² + c² + 2ab = 0
(d) a² – b² – 2ac = 0

Correct Answer is option (b)
Given that sin θ and cos θ are the roots of the equation ax² – bx + c = 0, so sin θ + cos θ = b/a and sin θ cos θ = c/a
Consider,
(sinθ + cos θ)² = sin²θ + cos²θ + 2 sin θ cos θ,
(b/a)² = 1 + 2(c/a) {using the identity sin²A + cos²A = 1}
b²/a² = 1 + (2c/a)
b² = a² + 2ac
a² – b² + 2ac = 0

Q.2. If tan A = 1/2 and tan B = 1/3, then the value of A + B is
(a) π/6
(b) π
(c) 0
(d) π/4

Correct Answer is option (d)
Given,
tan A = 1/2, tan B = 1/3
We know that,
tan(A + B) = (tan A + tan B)/(1 – tan A tan B)
= [(1/2) + (1/3)]/ [1 – (1/2)(1/3)]
= [(3 + 2)/6]/ [(6 – 1)/6]
= 5/5
= 1
= tan π/4
Therefore, A + B = π/4

Q.3. The value of cos 1° cos 2° cos 3° … cos 179° is
(a) 1/√2
(b) 0
(c) 1
(d) –1

Correct Answer is option (b)
cos 1° cos 2° cos 3° … cos 179°
cos 1° cos 2° cos 3° … cos 179°
= cos 1° cos 2° cos 3° … cos 89° cos 90° cos 91° … cos 179°
= cos 1° cos 2° cos 3° … cos 89° (0) cos 91° … cos 179°
= 0 {since the value of cos 90° = 0}

Q.4. The value of sin 50° – sin 70° + sin 10° is equal to
(a) 1
(b) 0
(c) 1/2
(d) 2

Correct Answer is option (b)
sin 50° – sin 70° + sin 10°
= sin(60° – 10°) – sin(60° + 10°) + sin 10°
Using the formulas
sin(A – B) = sin A cos B – cos A sin B
sin(A + B) = sin A cos B + cos A sin B, we get;
sin 50° – sin 70° + sin 10° = sin 60° cos 10° – cos 60° sin 10° – sin 60° + cos 10° – cos 60° sin 10° + sin 10°
= -2 cos 60° sin 10° + sin 10°
= -2 × (1/2) × sin 10° + sin 10°
= – sin 10° + sin 10°
= 0

Q.5. The value of sin (45° + θ) – cos (45° – θ) is
(a) 2 cosθ
(b) 2 sinθ
(c) 1
(d) 0

Correct Answer is option (d)
sin (45° + θ) – cos (45° – θ)
= sin (45° + θ) – sin (90° -(45° – θ)) {since sin(90° – A) = cos A}
= sin (45° + θ) – sin (45° + θ)
= 0
Alternative method:
sin (45° + θ) – cos (45° – θ)
Using the formulas
sin(A + B) = sin A cos B + cos A sin B
cos(A – B) = cos A cos B + sin A sin B, we get;
sin (45° + θ) – cos (45°– θ) = sin 45° cos θ + cos 45° sin θ – cos 45° cos θ – sin 45° sin θ
= (1/√2) cos θ + (1/√2) sin θ – (1/√2) cos θ – (1/√2) sin θ
= 0

Q.6. The value of tan 1° tan 2° tan 3° … tan 89° is
(a) 0
(b) 1
(c) 1/2
(d) Not defined

Correct Answer is option (b)
tan 1° tan 2° tan 3° … tan 89°
= [tan 1° tan 2° … tan 44°] tan 45°[tan (90° – 44°) tan (90° – 43°)… tan (90° – 1°)]
= [tan 1° tan 2° … tan 44°] [cot 44° cot 43°……. cot 1°] × [tan 45°]
= [(tan 1° × cot 1°) (tan 2° × cot 2°)…..(tan 44° × cot 44°)] × [tan 45°]
We know that,
tan A × cot A =1 and tan 45° = 1
Hence, the equation becomes as;
= 1 × 1 × 1 × 1 × …× 1
= 1 {As 1ⁿ = 1}

Q.7. If α + β = π/4, then the value of (1 + tan α) (1 + tan β) is
(a) 1
(b) 2
(c) – 2
(d) Not defined

Correct Answer is option (b)
Given,
α + β = π/4
Taking “tan” on both sides,
tan(α + β) = tan π/4
We know that,
tan(A + B) = (tan A + tan B)/(1 – tan A tan B)
and tan π/4 = 1.
So, (tan α + tan β)/(1 – tan α tan β) = 1
tan α + tan β = 1 – tan α tan β
tan α + tan β + tan α tan β = 1….(i)
(1 + tan α)(1 + tan β) = 1 + tan α + tan β + tan α tan β
= 1 + 1 [From (i)]
= 2

Q.8. If A lies in the second quadrant and 3 tan A + 4 = 0, then the value of (2 cot A – 5 cos A + sin A) is equal to
(a) -53/10
(b) 23/10
(c) 37/10
(d) 7/10

Correct Answer is option (b)
Given that A lies in the second quadrant and 3 tan A + 4 = 0.
3 tan A = -4
tan A = -4/3
cot A = 1/tan A = -3/4
Using the identity sec²A = 1 + tan²A,
sec²A = 1 + (16/9) = 25/9
sec A = √(25/9)
sec A = -5/3 (in quadrant II secant is negative)
cos A = 1/sec A = -⅗
Using the identity sin²A + cos²A = 1,
sin A = √(1 – 9/25) = √(16/25) = 4/5 (in quadrant II sine is positive)
Now,
2 cot A – 5 cos A + sin A
= 2(-3/4) – 5(-3/5) + (4/5)
= (-3/2) + 3 + (4/5)
= (-15 + 30 + 8)/10
= 23/10

Q.9. If for real values of x, cos θ = x + (1/x), then
(a) θ is an acute angle
(b) θ is right angle
(c) θ is an obtuse angle
(d) No value of θ is possible

Correct Answer is option (d)
Given,
cos θ = x + (1/x)
cos θ = (x² + 1)/x
⇒ x² + 1 = x cos θ
⇒ x² – x cos θ + 1 = 0
We know that for any real root of the equation ax² + bx + c = 0, b² – 4ac ≥ 0.
⇒ (-cos θ)² – 4 ≥ 0
⇒ cos²θ – 4 ≥ 0
⇒ cos²θ ≥ 4
⇒ cos θ ≥ ± 2
We know that -1 ≤ cos θ ≤ 1.
Hence, no value of θ is possible.

Q.10. Number of solutions of the equation tan x + sec x = 2 cos x lying in the interval [0, 2π] is
(a) 0
(b) 1
(c) 2
(d) 3

Correct Answer is option (c)
Given,
tan x + sec x = 2 cos x
(sin x/cos x) + (1/cos x) = 2 cos x
(sin x + 1)/cos x = 2 cos x
sin x + 1 = 2 cos²x
Using the identity sin²A + cos²A = 1,
sin x + 1 = 2(1 – sin²x)
sin x + 1 = 2 – 2 sin²x
⇒ 2 sin²x + sin x − 1 = 0
⇒ (2 sin x − 1)(sin x + 1)=0
⇒ sin x = −1, 1/2
⇒ x = π/6,5π/6,3π/2 ∈ [0, 2π]
But for x = 3π/2, tan x and sec x are not defined.
Therefore, there are only two solutions for the given equation in the interval [0, 2π].

Q.11. The value of sin 12°. sin48°.sin54° =
(a) 1/8
(b) 1/6
(c) 1/4
(d) 1/2

Correct Answer is option (a)
sin 12°. sin48°.sin54° =
=
=
=
=  

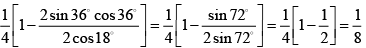
Q.12. The smallest positive value of x (in degrees) for which tan(x + 100°) = tan(x + 50°) tan x tan(x - 50°) is:
(a) 30°
(b) 45°
(c) 60°
(d) 90°

Correct Answer is option (a)
The relation may be written as
⇒
⇒
⇒
⇒ cos50°+ 2sin(2x + 50°) cos(2x + 50°) = 0
⇒ cos50°+ sin (4x + 100°) = 0 ⇒ cos50° + cos(4x + 10°)
= 0
⇒ cos(2x + 30°) cos(2x – 20°) = 0 ⇒ x = 30°, 55
⇒ The smallest value of x = 30°
Hence, (A) is the correct answer.

Q.13. If A + B + C = 180o then the value of tanA + tanB + tanC is :

(a) ≥ 3 √3
(b) ≥ 2 √3
(c) > 3 √3
(d) > 2 √3

Correct Answer is option (a)
tan(A + B) = tan( 180 – C)
or,
or, tanA + tanB + tanC = tana tanB tanC
 [since A.M. ≥ G.M.]
or,
or, tan² A tan² B tan² C ≥ 27 [cubing both sides]
or tanA tanB tanC ≥ 3 √3
⇒ tanA + tanB + tanC ≥ 3 √3.
Hence, (A) is the correct answer.

Q.14. Let 0 < A, B < π / 2 satisfying the equalities 3 sin² A + 2 sin² B = 1 and 3sin2A – 2sin2B = 0. Then A + 2B =:
(a) π / 4
(b) π / 3
(c) π / 2
(d) None of these.

Correct Answer is option (c)
From the second equation, we have

and from the first equality
3sin² A = 1 –2 sin² B = cos2B …(2)
Now cos (A + 2B) = cosA. cos2B – sinA . sin2B
= 3 cosA . sin² A – 3/2. sinA . sin2A
= 3cosA. sin² A – 3 sin² A . cosA = 0
⇒
Given that

Hence, A + 2B = π/2.
Hence, (C) is the correct answer.

Q.15. If a cos³ θ + 3a cos q sin² θ = x and a sin³ θ + 3a cos² θsin θ = y, then  (x + y)2/3 + (x – y)2/3
(a) 2a^2/3 
(b) a^2/3 
(c) 3a^2/3 
(d) 2a^1/3

Correct Answer is option (a)
a cos³ θ + 3a cos θ sin² θ = x
a sin³ θ  + 3a cos² θ sin θ  = y





Hence, (A) is the correct answer.

Q.16. If (1+ √1+ a ) tanα = 1+ √1- a , then  sin4a =
(a) a/2
(b) a
(c) a^2/3
(d) 2a

Correct Answer is option (b)
Let a = sin 4θ ⇒ √1+ a = cos 2θ + sin 2θ and √1- a = cos 2θ – sin 2θ

⇒
⇒
⇒
⇒
⇒ a = sin 4θ = sin (π – 4α) = sin 4α
Hence, (B) is the correct answer.

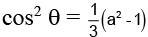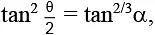Q.17. If  and  then  cos^2/3α + sin^2/3α =
(a) 2a^2/3
(b)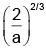
(c)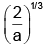
(d) 2a^1/3

Correct Answer is option (b)






Squaring and adding (1) and (2)


Hence, (B) is the correct answer.

Q.18. If 3 sin² α + 2 sin2 β = 1 and 3 sin 2α –2 sin 2β = 0, where α, β  are positive acute angles, then α + 2β =
(a) π/2
(b) π/3
(c) π/4
(d) π/6

Correct Answer is option (a)
3 sin2 α + 2 sin² β = 1 ……(1)
3 sin 2α = 2 sin ²β ……(2)
3 sin2 α = 1 – 2 sin² β = cos 2β
3 sin α sin α = cos 2β ……(3)
from equation (2)
3 . 2 sin α cos α = 2 sin 2β

from equation (3)

⇒ a + 2β = π/2.
Hence, (A) is the correct answer.

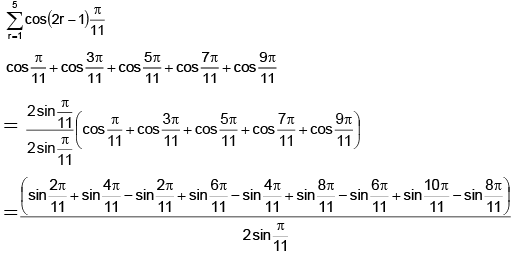
Q.19. The value of 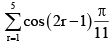 is:
(a) 1/2
(b) 1/3
(c) 1/4
(d) 1/6

Correct Answer is option (a)

=
Hence, (A) is the correct answer.

Q.20. If tanx = n. tany, n ∈ R⁺ , then maximum value of sec² (x - y) is equal to:
(a)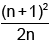
(b)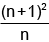
(c)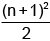
(d)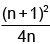

Correct Answer is option (d)
tanx = n tany, cos(x – y)
= cosx. cosy + sinx.siny.
⇒ cos(x – y) = cosx.cosy(1 + tanx.tany)
= cosx. cosy (1 + n tan²y)
⇒
=
=
=
Now,
⇒
⇒
Hence, (D) is the correct answer.