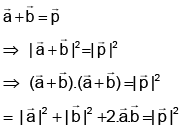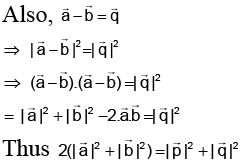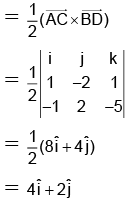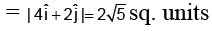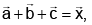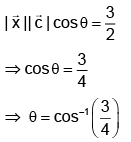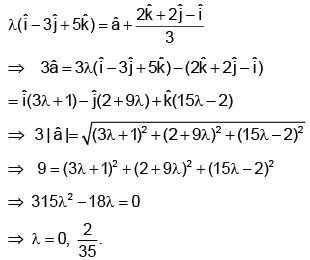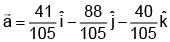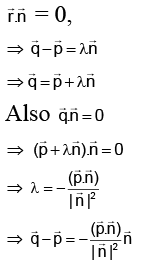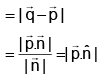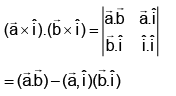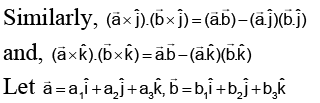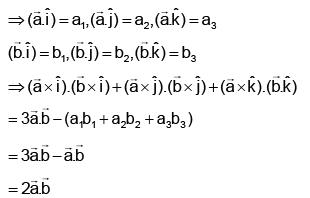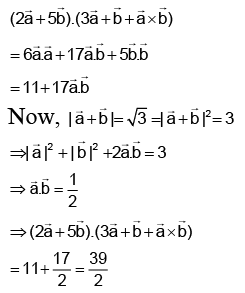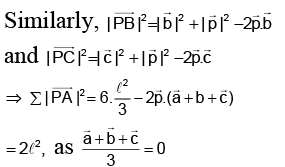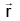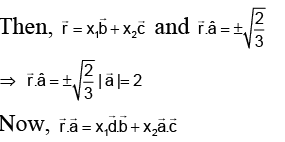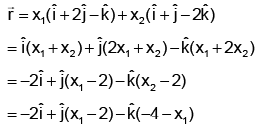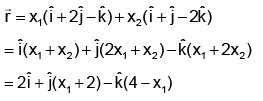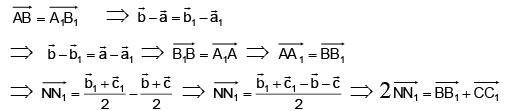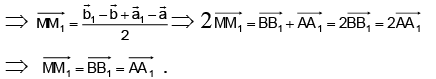JEE Advanced (Single Correct Type): Vector Algebra | Chapter-wise Tests for JEE Main & Advanced PDF Download

Q.1. What is the magnitude of vector -3i + 5j?
(a) √34
(b)√32
(c)√8
(d) √16

Correct Answer is option (a)
Vector, V = -3i + 5j
Magnitude of the vector, V;
|V| = √((-3)² + 5²) = √(9+25) = √34

Q.2. What is the value of x and y, if 2i + 3j = xi + yj?
(a) 4, 9
(b) 3, 2
(c) 2, 3
(d) 0, 0

Correct Answer is option (c)
Since,
2i + 3j = xi + yj
On comparing the two equations, we have;
x = 2 and y = 3

Q.3. The magnitude of the vector 6i + 2j + 3k is equal to:
(a) 5
(b) 1
(c) 7
(d) 12

Correct Answer is option (c)
Vector, V → 6i + 2j + 3k
Magnitude of the vector, V;
|V| = √(6² + 2² + 3²) = √(36+4+9) = √49 = 7

Q.4. Can two different vectors have the same magnitude?
(a) Yes
(b) No
(c) Cannot be determined
(d) None of the above

Correct Answer is option (a)
Two vectors can have the same magnitude.
Magnitude of vector i – 2j + k is equal to magnitude of vector 2i + j – k.

Q.5. The scalar product of 5i + j – 3k and 3i – 4j + 7k is:
(a) 15
(b) -15
(c) 10
(d) -10

Correct Answer is option (d)
Let A = 5i + j – 3k
B = 3i – 4j + 7k
A . B = (5i + j – 3k).(3i – 4j + 7k)
= 5 · 3 + 1 · (-4) + (-3) · 7
= 15 – 4 – 21
= -10

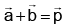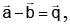Q.6. If  and  then:
(a)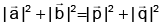
(b)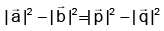
(c)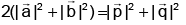
(d)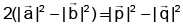

Correct Answer is option (c)


Hence, (c) is correct answer.

Q.7. ABCD is a parallelogram with 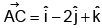 and 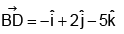. Area of this parallelogram is equal to:
(a) √5/2 sq. units
(b) 2√5 sq. units
(c) 4√5 sq. units
(d) √5 sq. units

Correct Answer is option (b)
Area vector of parallelogram

∴ Area of the parallelogram

 Hence, (b) is correct answer.

Q.8. Let 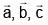 be unit vectors such that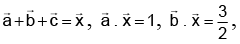 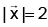. Then angle between c and x is :
(a) cos^-1(1/4)
(b) cos^-1(3/4)
(c) cos^-1(3/8)
(d) cos^-1(5/4)

Correct Answer is option (b)

Taking dot with  on both sides, we get

If 'θ' be the angle between  then

Hence, (b) is correct answer.

Q.9. If the vector 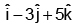 bisects the angle between  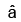and 

 where 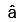 is a unit vector, then:
(a)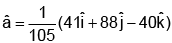
(b)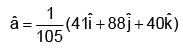
(c)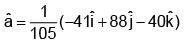
(d)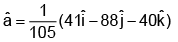

Correct Answer is option (d)
We must have

For l = 0,  (not acceptable)
For λ = 2/35,

Hence, (d) is correct answer.

Q.10. Distance of 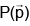  from the plane  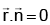is:
(a)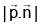
(b)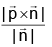
(c)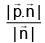  
(d) None of these

Correct Answer is option (c)
Let  be the foot of altitude drawn from P to the plane

∴ Required distance

Hence, (c) is correct answer.

Q.11. For any two vectors 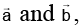, the expression  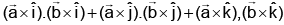is always equal to:
(a)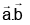
(b)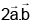
(c) Zero
(d) None of these

Correct Answer is option (b)



Hence, (b) is correct answer.

Q.12. Let 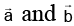 be unit vectors such that  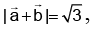then the value of  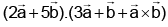is equal to:
(a) 11/2
(b) 13/2
(c) 39/2
(d) 23/2

Correct Answer is option (c)

Hence, (c) is correct answer.

Q.13. Let P is any arbitrary point on the circumcircle of a given equilateral triangle of side length 'ℓ' units then, 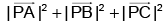 is always equal to:
(a) 2ℓ²
(b) 2√3ℓ²
(c) ℓ²
(d) 3ℓ²

Correct Answer is option (a)
Let P.V. of P, A, B and C are  respectively and  be the circumcentre of the equilateral triangle ABC.


Hence, (a) is correct answer.

Q.14. 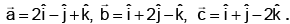 A vector coplanar with 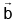and 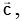 whose projection on  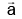is of magnitude √2/3 is :
(a)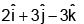
(b)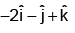
(c)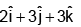
(c)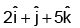

Correct Answer is option (a)
Let the required vector be

⇒ ±2 = x₁ (2 - 2 - 1) + x₂ (2 - 1 - 2)
⇒ x₁ + x₂ = -2,  or 2
If x₁ + x₂ = -2 , then

where x₁ ∈ R.
If x₁ + x₂ = 2, then

Hence, (a) is correct answer.

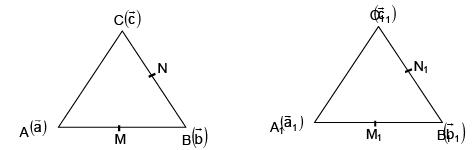
Q.15. Consider ΔABC  and  ΔA₁B₁C₁ in such a  way  that 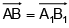 and  M, N, M₁ , N, be  the  mid points of  AB, BC, A₁B₁ and B₁C₁ respectively,  then
(a)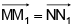
(b)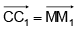
(c)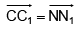
(d)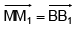

Correct Answer is option (d)



Hence, (d) is correct answer.