JEE Advanced (Subjective Type Questions): Definite Integrals & Applications of Integrals - 2 | Chapter-wise Tests for JEE Main & Advanced PDF Download

Clear all your JEE doubts with EduRev Join for Free

Join for Free

Q. 17. If f and g are continuous function on [0, a] satisfying f(x) = f(a – x) and g(x) + g(a – x) = 2, then show that          (1989 - 4 Marks)

Solution. 

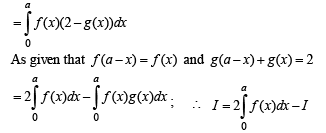
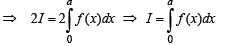
Hence the result.

Q. 18. Show that 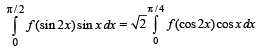              (1990 -  4 Marks)

Solution. 

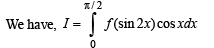              ...(1)
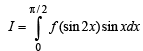               ...(2)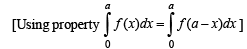

Adding (1) and (2), we get

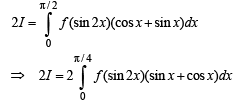
[Using the property,

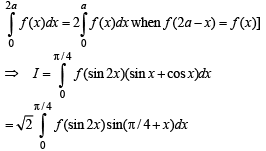
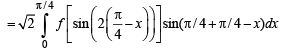
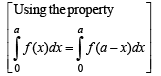
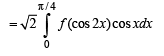Hence Proved.

Q. 19. Prove that for any positive integer k,  2[cos x + cos 3x + .............. + cos (2k – 1) x]              (1990 -  4 Marks)

Hence prove that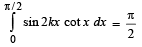  

Solution. To prove :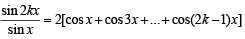 

It is equivalent to prove that

sin 2kx = 2 sin x cos x + 2 cos 3x sinx+ ... + 2 cos(2k- 1) x sinx

Now, R.H.S. = (sin2 x) + (sin4 x- sin2x) + (sin6 x- sin4x) +.... +(sin 2kx - sin(2k- 2)x)

= sin2kx = L.H.S. Hence Proved.

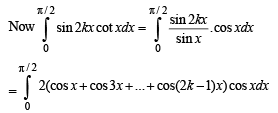
[Using the identity proved above]

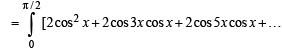 +2 cos(2k- 1) x cos x]dx 

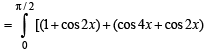 +(cos 6 x + cos 4x) + (cos 2kx) + cos(2k- 2) x ]dx

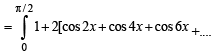cos(2k- 2)x] + cos 2 k x dx

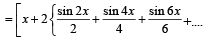
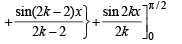
= π /2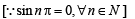 

Hence Proved

Q. 20. Compute the area of the region bounded by the curves y = ex In x and                (1990 -  4 Marks)

Ans.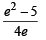 

Solution. The given curves are

y = ex logex … (1)

and 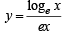            … (2)

The two curves intersect where ex log x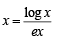 

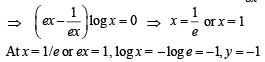
At x = 1/e or ex = 1, log x = - log e =-1,y =-1 

So that 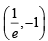  is one point of intersection and at x = 1,
log 1 = 0 ∴  y = 0 

∴ (1, 0) is the other common point of intersection of the curves. Now in between these two points,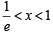  

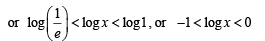
i.e. log x is – ve, throughout 

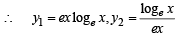
Clearly under the condition stated above y₁ < y₂ both being –ve in the interval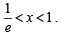 

The rough sketch of the two curves is as shown in fig. and shaded area is the required area.

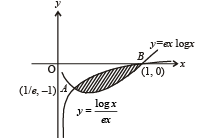
∴ The required area = shaded area

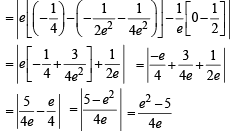
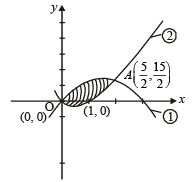
Q. 21. Sketch the curves and identify the region bounded by x = 1/2, x = 2, y = In x and y = 2^x.  Find the area of this region.            (1991 -  4 Marks)

Ans. 

Solution. The given curves are x = 1/2 ....(1), x = 2...(2), y = ln x...(3),y = 2^x....(4)

Clearly (1) and (2) represent straight lines parallel to y - axis at distances 1/2 and 2 units from it, respectively. Line x = 1/2 meets   meets (3) at (2, ln 2) and (4) at (2, 4).

The graph of curves are as shown in the figure.

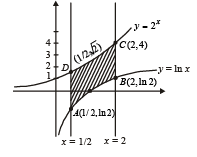
Required area = ABCDA

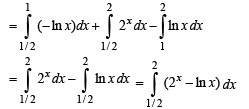
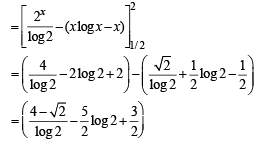
Q. 22. If ‘f’ is a continous function with 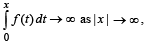 then show that every line y = mx 

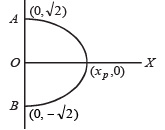
intersects the curve 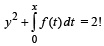                (1991 -  4 Marks)

Solution. We are given that f is a continuous function and

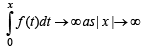
To sh ow that ever y line y = mx intersects the curve

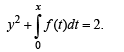
If possible, let y = mx intersects the given curve, then Substituting y = mx in the equation of the curve we get

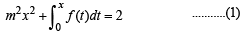
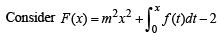
Then F (x) is a continuous function as f (x) is given to be continuous.

Also F ( x) → ∞ as |x|→ ∞

But F (0) = –2

Thus F (0) = –ve and F(b) = +ve where b is some value of x, and F (x) is continuous.

Therefore F (x) = 0 for some value of x Î (0,b) or eq. (1) is solvable for x.

Hence y = mx intersects the given curve.

Q. 23. 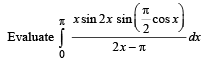                 (1991 -  4 Marks)

Ans. 

Solution.

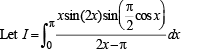
Consider, 2x - p = y n ⇒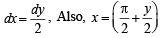  

When x → 0,y → -π when x → π ,y → π

∴ We get

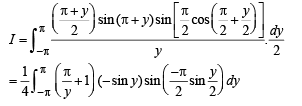
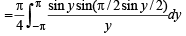
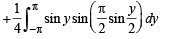
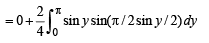
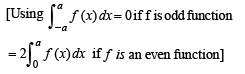
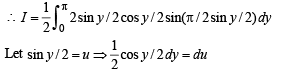
⇒ cos y / 2 dy = 2du

Also as y → 0,u → 0 and as y → π,u → 1

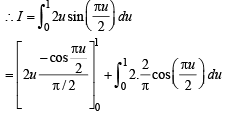
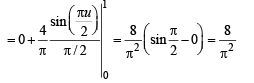
Q. 24. Sketch the region bounded by the curves y = x² and 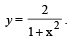 Find the area.             (1992 -  4 Marks)

Ans.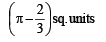 

Solution. The given curves are y = x² and 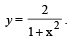 Here y = x² is upward parabola with vertex at origin.

Also, 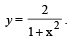 is a curve symm. with respect to y-axis.

At x = 0,y = 2

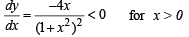
∴ Curve is decreasing on (0, ∞)

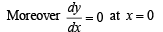
⇒ At (0,2) tangent to curve is parallel to x – axis.
As x → ∞ , y → 0

∴ y = 0 is asymptote of the given curve.

For the given curves, point of intersection : solving their equations we get x = 1, y = 1, i.e., (1,1).

Thus the graph of two curves is as follows:

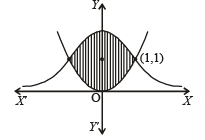
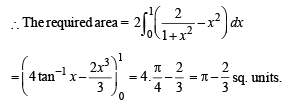
Q. 25. Determine a positive integer n < 5,such that 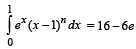              (1992 -  4 Marks)

Ans. n = 3

Solution. Given that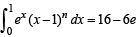   

where n ∈ N and  n < 5

To find the value of n.

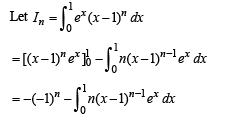
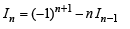  .........(1)

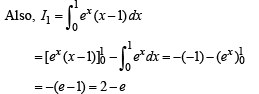
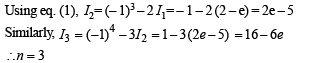
Q. 26.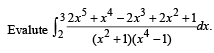              (1993 -  5 Marks)

Ans.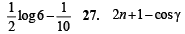 

Solution. 

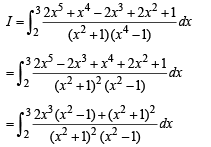
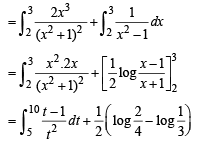
Put x² + 1 = t ,2 x dx = dt

when x → 2,t → 5 , x → 3,t → 10

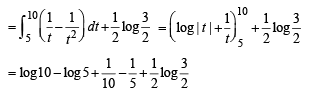
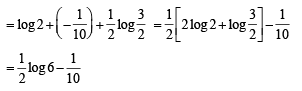
Q. 27. Show that 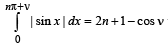where n is a positive integer and 0 < n < π.            (1994 -  4 Marks)

Ans. 2n + 1 - cosγ 

Solution. To prove that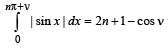 

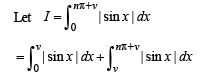
Now we know that | sin x| is a periodic function of period π , So using the property..

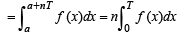
where  n ∈ I and f (x) is a periodic function of period T 

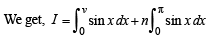
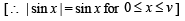
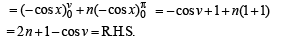
Q. 28. In what ratio does the x-axis divide the area of the region bounded by the parabolas y = 4x – x² and y = x² – x ?             (1994 -  5 Marks)

Ans. 121 : 4

Solution. The given equations of parabola are 

y = 4 x - x² or (x - 2)² = -(y- 4)          ..... (1)

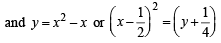            ...... (2)

Solving the equations of two parabolas we get their points of intersection as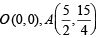 

Here the area below x - axis,

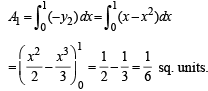
Area above x - axis,

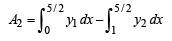
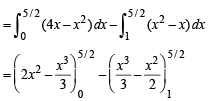
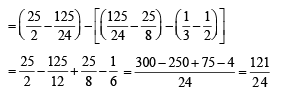
∴ Ratio of areas above x – axis and below x – axis.

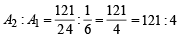
Q. 29. 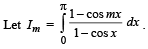Use mathematical induction to prove that I_m = m π , m = 0, 1, 2, .......           (1995 -  5 Marks)

Solution. Given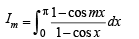 

To prove: I_m = mπ,m= 0, 1, 2, ......
For m = 0

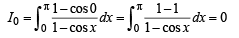
∵ Result is true for m = 0

For m = 1,

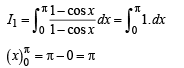
∴ Result is true for m = 1

Let the result be true for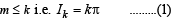  

Consider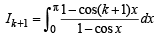 

Now, 1 - cos(k+ 1)x
= 1 – cos kx cosx + sin kx sin x
= 1 + cos kx cos x + sin kx sin x – 2 cos kx cos x
= 1 + cos (k – 1) x – 2 cos kx cos x
= 2 – (1 – cos (k – 1) x) –2 cos kx cos x
= 2 (1 – cos kx cos x) – (1– cos (k – 1) x)
= 2 – 2 cos kx + 2 cos kx – 2 cos kx cos x – [1– cos ( k – 1) x]
= 2 (1 – cos kx) + 2 cos kx (1– cos x) – (1 – cos (k – 1) x)

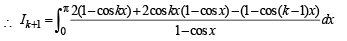
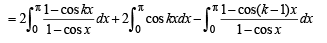
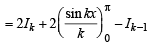
= 2 (kπ) + 2(0) - (k - 1)π [Using (i)]
= 2kπ- kπ+π = (k +1)π

Thus result is true for m=k  + 1 as well. Therefore by the principle of mathematical induction, given statement is true for all m = 0, 1, 2, ...............

Q. 30. Evaluate the definite integral : 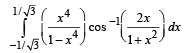             (1995 -  5 Marks)

Ans.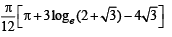 

Solution.

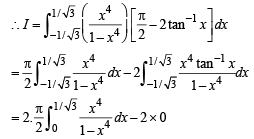
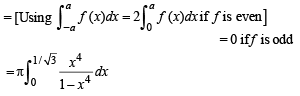
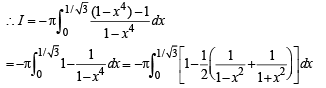
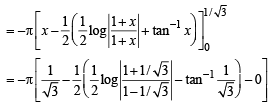
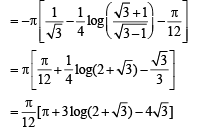
Q. 31. Consider a square with vertices at (1, 1), (– 1, 1), (– 1, – 1) and (1, – 1). Let S be the region consisting of all points inside the square which are nearer to the origin than to any edge. Sketch the region S and find its area.            (1995 -  5 Marks)

Ans.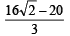 

Solution. Let us consider any point P (x, y) inside the square such that its distance from origin < its distance from any of the edges say AD

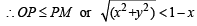
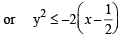              ........ (1)

Above represents all points within and on the parabola 1. If we consider the edges BC then OP < PN will imply

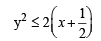            ........ (2)

Similarly if we consider the edges AB and CD, we will have 

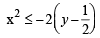             ........ (3)

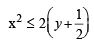              ........ (4)

Hence S consists of the region bounded by four parabolas meeting the axes at 

The point L is intersection of P₁ and P₃ given by (1) and (3).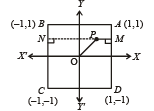

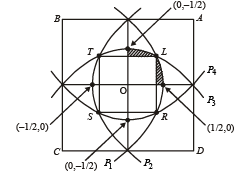
y² - x² = -2( x - y) = 2( y-x) 0
∴ y - x = ∴ y = x ∴ x² + 2x - 1 = 0 ⇒  (x + 1)² = 2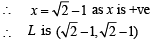

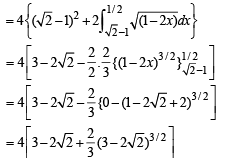
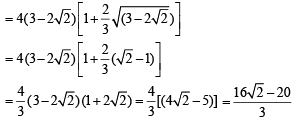
Q. 32. Let A_n be the area bounded by the curve y = (tan x)n and the lines x = 0, y = 0 and x = π/4.  Prove that for n > 2, 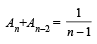  and deduce  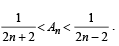                (1996 - 3 Marks)

Solution.

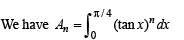
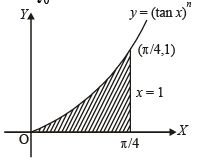
Since 0 < tan x < 1, when 0 < x < π /4 , we have 

0 < (tan x)^{n +1} < (tanx)n for each n ∈ N

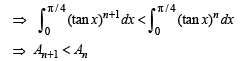
Now, for n > 2

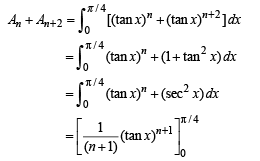
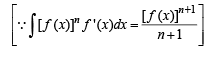
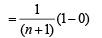
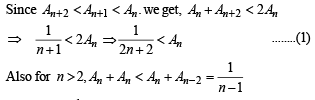
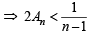
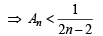                 ........(2)

Combining (1) and (2) we get 

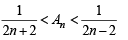 Hence Proved.