JEE Advanced (Subjective Type Questions): Definite Integrals & Applications of Integrals - 3 | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q. 33. Determine the value of 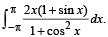 (1997 - 5 Marks)
(1997 - 5 Marks)
Ans. π2
Solution.
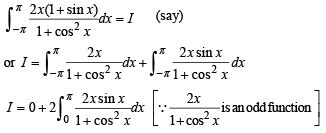
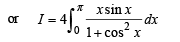 .....(1)
.....(1)
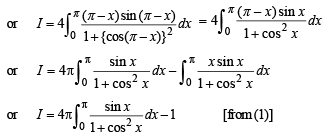
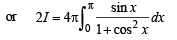
Putting cos x = t, – sin x dx = dt
When x → 0,t →1 and when x → p,t → -1
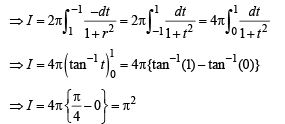
Q. 34. Let f(x) = Maximum {x2, (1 – x)2, 2x(1 – x)}, where 0 < x < 1. Determine the area of the region bounded by the curves y = f(x), x-axis, x = 0 and x = 1.
Ans. 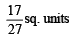
Solution. We draw the graph of y = x2, y = (1– x)2 and y = 2x (1– x) in figure.
Let us find the point of intersection of y = x2 and y = 2x (1– x)
The x – coordinate of the point of intersection satisfies the equation x2 = 2x (1– x), ⇒ 3x2 = 2x ⇒ 0 or x = 2 /3
∴ At B, x = 2/3
Similarly, we find the x coordinate of the points of intersection of y = (1 – x)2 and y = 2x (1– x) are x = 1/3 and x = 1
∴ At A, x = 1/3 and at C x = 1

From the figure it is clear that
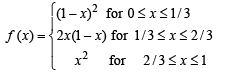
The required area A is given by
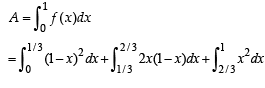
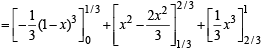
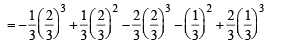
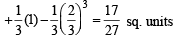
Q. 35. Prove that 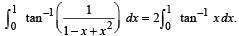 Hence or otherwise, evaluate the integral
Hence or otherwise, evaluate the integral 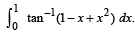
Ans. log 2
Solution.
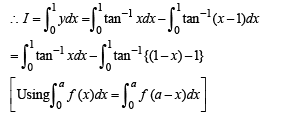
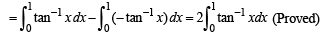
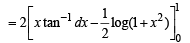
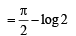 ...... (1)
...... (1)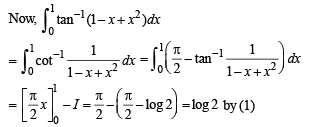
Q. 36. Let C1 and C2 be the graphs of the functions y = x2 and y = 2x, 0 < x < 1 respectively. Let C3 be the graph of a function y = f(x), 0 < x < 1, f(0) = 0. For a point P on C1, let the lines through P, parallel to the axes, meet C2 and C3 at Q and R respectively (see figure.) If for every position of P (on C1), the areas of the shaded regions OPQ and ORP are equal, determine the function f(x).
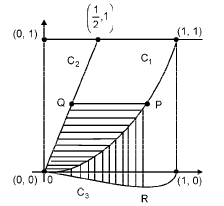
Ans. f (x) = x3-x2
Solution. f (x) = x3-x2
Let P be on C1, y = x2 be (t, t2)
∴ ordinate of Q is also t2.
Now Q lies on y = 2x, and y = t2
∴ x = t2/2
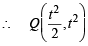
For point R, x = t and it is on y = f (x)
∴ R is [t, f (t)]
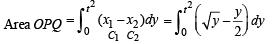
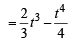 ...(1)
...(1)
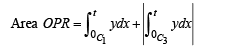
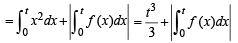
Equating (1) and (2), we get,

Differentiating both sides,we get,
t2 - t3 =- f (t)
∴ f (t) = x3 - x2.
Q. 37. 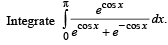
Ans. π/2
Solution.
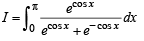
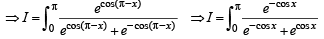
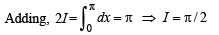
Q. 38. Let f(x) be a continuous function given by 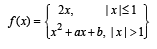
Ans. 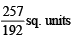
Solution.
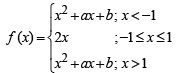
∵ f (x) is continuous at x = – 1 and x = 1
∴ (–1)2 + a (–1) + b = – 2 and 2 = (1)2 + a . 1 + b i.e. a – b = 3 and a + b = 1
On solving we get a = 2, b = –1
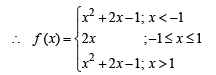
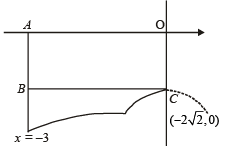
Given curves are y = f (x), x = – 2y2 and 8x + 1 = 0
Solving x = – 2 y2 , y = x2 + 2x –1 (x < –1) we get x = – 2
Also y = 2x, x = – 2 y2 meet at (0, 0)
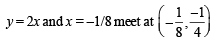
The required area is the shaded region in the figure.
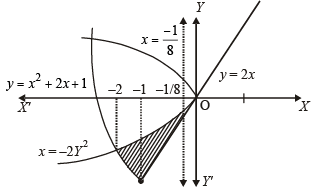
∴ Required area
NOTE THIS STEP :
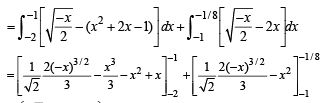
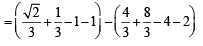
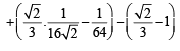
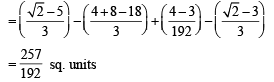
Q. 39. For x > 0, let 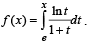 Find the function
Find the function 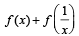
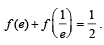
Here, lnt = loget.
Solution.
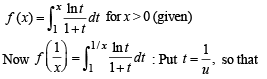
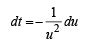
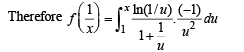
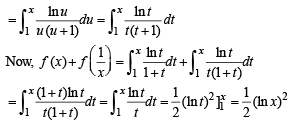
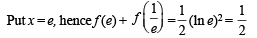
Hence Proved.
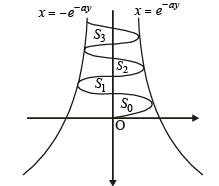
Q. 40. Let b ≠ 0 and for j = 0, 1, 2, …, n, let Sj be the area of the region bounded by the y-axis and the curve xeay = sin by, 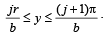 Show th at S0, S1, S2, …, Sn are in geometric progression. Also, find their sum for a = -1 and b = π.
Show th at S0, S1, S2, …, Sn are in geometric progression. Also, find their sum for a = -1 and b = π.
Ans. 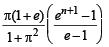
Solution. Given that x = sin by. e-ay ⇒ – e–ay < x < e–ay
The figure is drawn taking a and b both +ve. The given curve oscillates between x = e–ay and x = – e–ay
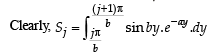
Integrating by parts, 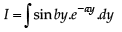
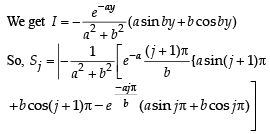
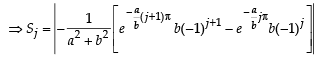
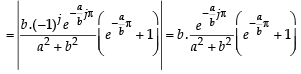
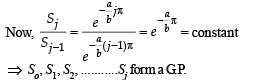
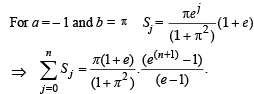
Q. 41. Find the area of the region bounded by the curves y = x2, y = |2 – x2| and y = 2, which lies to the right of the line x = 1.
Ans. 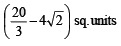
Solution. The given curves are y = x2 which is an upward parabola with vertex at (0, 0)
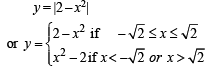
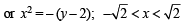 .......(2)
.......(2)
a downward parabola with vertex at (0, 2)
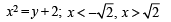 ..........(3)
..........(3)
An upward parabola with vertex at (0, – 2)
y = 2 .........(4)
A straight line parallel to x – axis
x = 1 ..........(5)
A straight line parallel to y – axis
The graph of these curves is as follows.
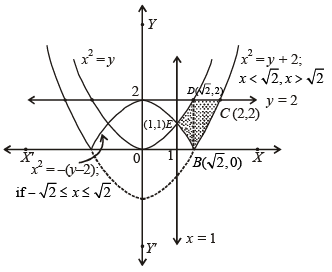
∴ Required area = BCDEB
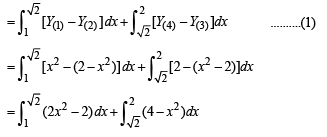
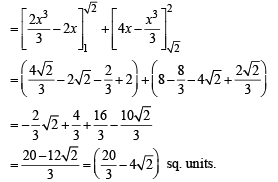
Q. 42. If f is an even function then prove that
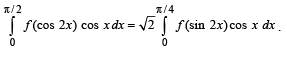
Solution. Given that f (x) is an even function, then to prove
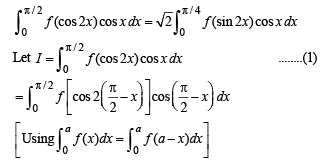
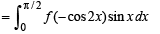
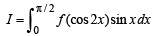 .......(2)
.......(2)
[As f is an even function] Adding two values of I in (1) and (2) we get
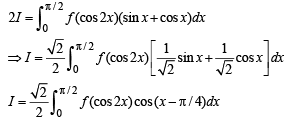
Let x - π /4 = t so that dx = dt
as x → 0, t → -π /4 and as x → π/4, t → π/2-π/4 = π/4
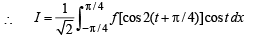
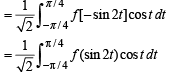
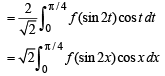
R.H.S. Hence proved.
Q. 43. 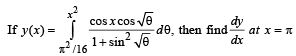
Ans. 2π
Solution. We have,
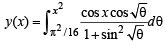
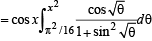
[∵ cos x is independent of θ]
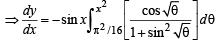
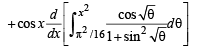
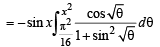
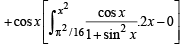 (Using Leibnitz thm.)
(Using Leibnitz thm.)
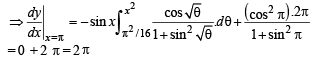
Q. 44. Find the value of 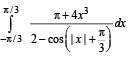
Ans. 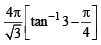
Solution.
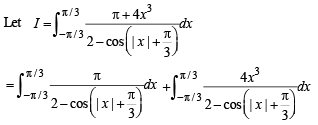
The second integral becomes zero integrand being an odd function of x.
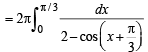
{using the prop. of even function and also |x| = x for 0 < x < π /3}
Let x + π /3 = y ⇒ dx = dy
also as x → 0,y → π /3 as x → π /3 , y → 2π /3
∴ The given integral becomes
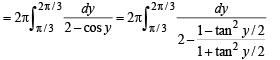
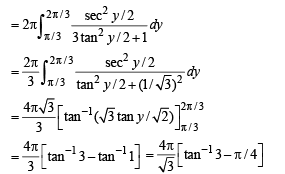
Q. 45. 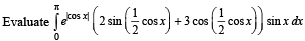
Ans. 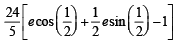
Solution. Let
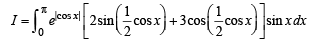
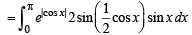
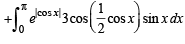
= I1+I2
Now using the property that
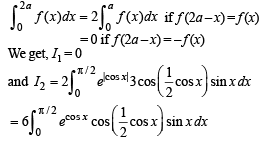
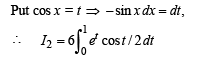
Integrating by parts, we get
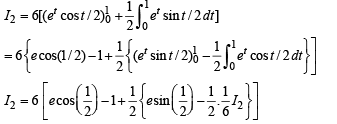
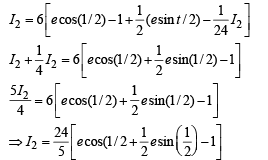
Q. 46. Find the area bounded by the curves x2 = y, x2 = –y and y2 = 4x – 3.
Ans. 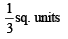
Solution. The given curves are, x2 = y .........(i)
x2 = – y .........(ii)
y2 = 4 x –3 .........(iii)
Clearly point of intersection of (i) and (ii) is (0, 0). For point of intersection of (i) and (iii), solving them as follows
x4 -4x+3 = 0 (x-1)(x3 + x2 +x-3) = 0
or ( x - 1)2 ( x2 + 2x + 3)= 0 ; ⇒ x = 1 and then y = 1
∴ Req. point is ( 1, 1). Similarly point of intersection of (ii) and (iii) is (1, – 1). The graph of three curves is as follows:
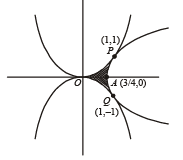
We also observe that at x = 1 and y = 1
 for (i) and (iii) is same and hence the two curves touch each other at (1, 1).
for (i) and (iii) is same and hence the two curves touch each other at (1, 1).
Same is the case with (ii) and (iii) at (1, –1).
Required area = Shaded region in figure = 2 (Ar OPA)
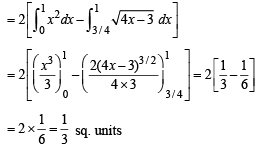
Q. 47. f(x) is a differ en tiable function an d g(x) is a dou ble differentiable function such that |f(x)| < 1 and f '(x) = g(x). If f2(0) + g2(0) = 9. Prove that there exists some c∈ (-3, 3) such that g (c).g ''(c) < 0 .
Solution. Given that f (x) is a differentiable function such that f’(x) = g (x), then
Similarly
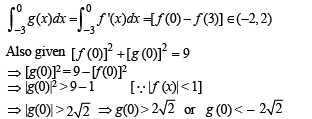
First let us consider g (0) > 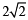
Let us suppose that g'' (x) be positive for all x ∈ (–3, 3).
Then g” (x) > 0 ⇒ the curve y = g (x) is open upwards.
Now one of the two situations are possible. (i) g(x) is increasing
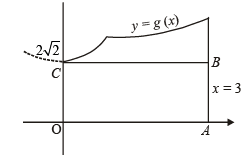
a contradiction as 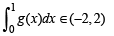
∴ at least at one of the point c ∈ (–3,3), g'' (x) < 0.
But g (x) > 0 on (– 3, 3)
Hence g(x) g''(x) < 0 at some x ∈ (– 3, 3).
(ii) g (x) is decreasing
a contradiction as 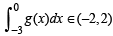
∴ at least at one of point c ∈ (-3, 3) g "(x) should be – ve. But g(x) > 0 on (–3 , 3).
Hence g (x) g'' (x) < 0 at some x ∈ (–3 , 3).
Secondly let us consider g (0) < 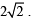
Let us suppose that g'' (x) be – ve on (– 3 , 3). then g'' (x) < 0 ⇒ the curve y = g(x) is open downward.
Again one of the two situations are possible (i) g (x) is decreasing then
a contradiction as 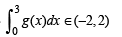
∴ At least at one of the point c ∈ (– 3, 3), g'' (x) is + ve. But g (x) < 0 on (– 3, 3).
Hence g(x) g'' (x) < 0 for some x ∈ (– 3, 3).
(ii) g (x) is increasing then
a contradiction as as 
∴ At least at one of the point c ∈ (– 3, 3) g'' (x) is + ve.
But g (x) < 0 on ( –3, 3).
Hence g (x) g'' (x) < 0 for some x ∈ (– 3,3).
Combining all the cases, discussed aboe, we can conclude that at least at one point in (– 3, 3), g (x) g”(x) < 0.
Q. 48. 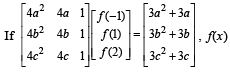 is a quadratic function and its maximum value occurs at a point V. A is a point of intersection of y = f(x) with x-axis and point B is such that chord AB subtends a right angle at V. Find the area enclosed by f(x) and chord AB.
is a quadratic function and its maximum value occurs at a point V. A is a point of intersection of y = f(x) with x-axis and point B is such that chord AB subtends a right angle at V. Find the area enclosed by f(x) and chord AB.
Ans. 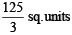
Solution. 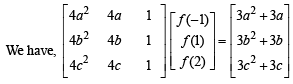
⇒ 4a2 f (-1) + 4af(1) + f (2) =3a2+ 3a
4b2 f (-1) + 4bf (1) + f (2) = 3b2+3a
4c2 f (-1) + 4cf (1) + f (2) = 3c2+3c
Consider the equation
4 x2 f (-1) + 4 xf (1) + f (2) = 3x2+3x or
[4 f (-1) - 3]x2 + [4 f (1) - 3]x +f (2)= 0
Then clearly this eqn. is satisfied by x = a,b,c
A quadratic eqn. satisfied by more than two values of x means it is an identity and hence
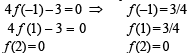
Let f (x) = px2 +qx +r [f (x) being a quadratic eqn.]
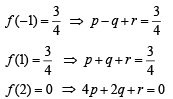
Solving the above we get 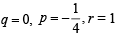
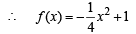
It’s maximum value occur at f’ (x) = 0 i.e., x = 0 then f (x) = 1, ∴ V ( 0, 1)
Let A (–2, 0) be the point where curve meet x –axis.

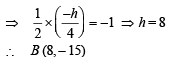
Equation of chord AB is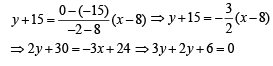
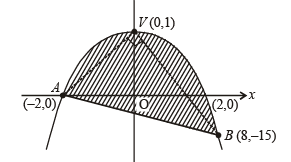
Required area is the area of shaded region given by
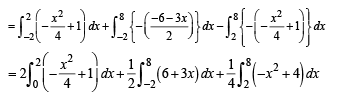
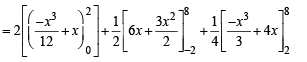
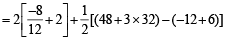
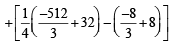
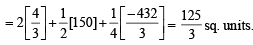
Q. 49. 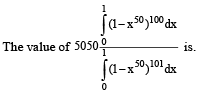
Solution.
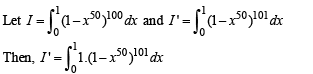
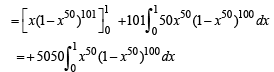
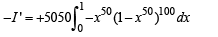
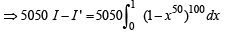
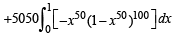
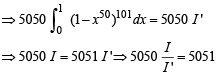
|
481 docs|964 tests
|
















