JEE Advanced (Subjective Type Questions): Structure of Atom | Chapter-wise Tests for JEE Main & Advanced PDF Download
Q.1. Naturally occurring boron consists of two isotopes whose atomic weights are 10.01 and 11.01. The atomic weight of natural boron is 10.81. Calculate the percentage of each isotope in natural boron. (1978)
Ans. Sol.
Let the % of isotope with At. wt. 10.01 = x
∴ % of isotope with At. wt. 11.01 = (100 – x)
At. wt. of boron = 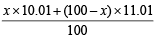
⇒ 10.81 = 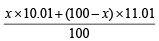 ∴ x = 20
∴ x = 20
Hence % of isotope with At. wt. 10.01 = 20%
∴ % of isotope with At. wt. 11.01 = 100 – 20 = 80%.
Q. 2. The energy of the electron in the second and the third Bohr ’s orbits of the hydrogen atom is –5.42 × 10–12 erg and –2.41 × 10–12 erg respectively. Calculate the wavelength of the emitted radiation when the electron drops from the third to the second orbit. (1981 - 3 Marks)
Ans. Sol. TIPS/Formulae :
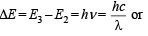
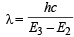
Given E2 = – 5.42 × 10–12 erg, E3 = – 2.41 × 10–12 erg
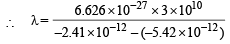
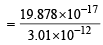 = 6.604 × 10–5 cm = 6.604Å
= 6.604 × 10–5 cm = 6.604Å
Q.3. Calculate the wavelength in Angstrom of the photon that is emitted when an electron in the Bohr orbit, n = 2 returns to the orbit, n = 1 in the hydrogen atom. The ionization potential of the ground state hydrogen atom is 2.17 × 10–11 erg per atom. (1982 - 4 Marks)
Ans. Sol. TIPS/Formulae : (i) Energy of nth orbit = 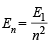
(ii) Difference in energy = 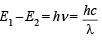
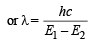
Given E1 = 2.17 × 10–11
∴ Energy of second orbit = 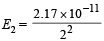
= 0.5425 × 10–11 erg
ΔE = E1 – E2 = 2.17 × 10–11 – 0.5425 × 10–11
= 1.6275 × 10–11 erg
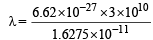 = 12.20 × 10–6 cm = 1220 Å
= 12.20 × 10–6 cm = 1220 Å
Q.4. The electron energy in hydrogen atom is given by E = (–21.7 × 10–12)/n2 ergs. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength (in cm) of light that can be used to cause this transition? (1984 - 3 Marks)
Ans. Sol. TIPS/Formulae : To calculate the energy required to remove electron from atom, n = ∞ is to be taken.
Energy of an electron in the nth orbit of hydrogen is given by
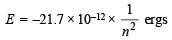
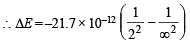
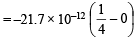
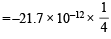
= – 5.42 × 10–12 ergs
Now we know that ΔE = hv
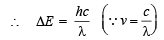 or
or 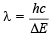
Substituting the values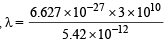
= 3.67 × 10–5 cm
Q.5. Give reasons why the ground state outermost electronic configuration of silicon is : (1985 - 2 Marks)
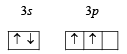 and not
and not 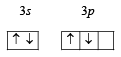
Ans. Sol. Ground state electronic configuration of Si
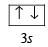
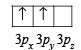
is in accordance with Hund’s rule which states that electron pairing in any orbital (s, p, d or f) cannot take place until each orbital of the same sub-level contains 1 electron each of like spin.
Q.6. What is the maximum number of electrons that may be present in all the atomic orbitals with principal quantum number 3 and azimuthal quantum number 2? (1985 - 2 Marks)
Ans. Sol. For n = 3 and l = 2 (i.e., 3d orbital), the values of m varies from –2 to +2, i.e. –2, –1, 0, +1, +2 and for each ‘m’ there are 2 values of ‘s’, i.e. +½ and –½. ∴ Maximum no. of electrons in all the five d-orbitals is 10.
Q.7. According to Bohr’s theory, the electronic energy of hydrogen atom in the nth Bohr’s orbit is given by
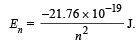 Calculate the longest wavelength of light that will be needed to remove an electron from the third Bohr orbit of the He+ ion. (1990 - 3 Marks)
Calculate the longest wavelength of light that will be needed to remove an electron from the third Bohr orbit of the He+ ion. (1990 - 3 Marks)
Ans. Sol. En of H =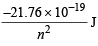
∴ En of He+ = 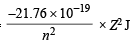
∴ E3 of He+ =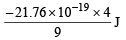
Hence energy equivalent to E3 must be supplied to remove the electron from 3rd orbit of He+. Wavelength corresponding to this energy can be determined by applying the relation.
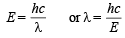
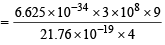
= 2055 × 10–10 m = 2055 Å
Q.8. Estimate the difference in energy between Ist and 2nd Bohr orbit for a hydrogen atom. At what minimum atomic number, a transition from n = 2 to n = 1 energy level would result in the emission of X -rays with l = 3.0 x10-8 m ? Which hydrogen atom-like species does this atomic number correspond to ? (1993 - 5 Marks)
Ans. Sol. TIPS/Formulae : 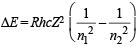
Here, R = 1.0967 × 107 m–1 h = 6.626 × 10–34 J sec, c = 3 × 108 m/sec
n1 = 1, n2 = 2 and for H-atom, Z = 1
E2 – E1 = 1.0967 × 107 × 6.626 × 10–34 × 3 × 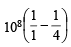
ΔE = 1.0967 × 6.626 × 3 × 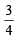 × 10–19 J
× 10–19 J
= 16.3512 × 10–19 J
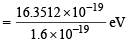 = 10.22 eV
= 10.22 eV
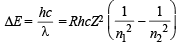
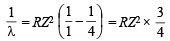
Given, λ = 3 × 10–8 m
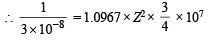
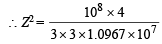
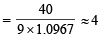 ∴ Z = 2
∴ Z = 2
So it corresponds to He+ which has 1 electron like hydrogen.
Q.9. What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition n = 4 to n = 2 of He+ spectrum? (1993 - 3 Marks)
Ans. Sol. For He+ ion, we have
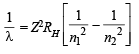
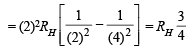 ...(i)
...(i)
Now for hydrogen atom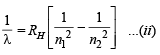
Equating equations (i) and (ii), we get
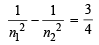
Obviously, n1 = 1 and n2 = 2
Hence, the transition n = 2 to n = 1 in hydrogen atom will have the same wavelength as the transition, n = 4 to n = 2 in He+ species.
Q.10. Find out the number of waves made by a Bohr electron in one complete revolution in its 3rd orbit. (1994 - 3 Marks)
Ans. Sol. TIPS/Formulae : Number of waves = 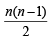
where n = Principal quantum number or number of orbit
Number of waves =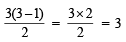
Q.11. Iodine molecule dissociates into atoms after absorbing light of 4500 Å . If one quantum of radiation is absorbed by each molecule, calculate the kinetic energy of iodine atoms. (Bond energy of I2 = 240 kJ mol–1) (1995 - 2 Marks)
Ans. Sol. Bond energy of I2 = 240 kJ mol–1 = 240 × 103 J mol–1
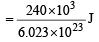 molecule–1
molecule–1
= 3.984 × 10–19 J molecule–1
Energy absorbed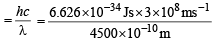
= 4.417 ×10–19 J
Kinetic energy = Absorbed energy – Bond energy
∴ Kinetic energy = 4.417 × 10–19 – 3.984 ×10–19 J
= 4.33 × 10–20 J
∴ Kinetic energy of each atom of iodine
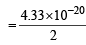 = 2.165 x 10 -20
= 2.165 x 10 -20
Q. 12. Calculate the wave number for the shortest wavelength transition in the Balmer series of atomic hydrogen. (1996 - 1 Mark)
Ans. Sol. The shortest wavelength transition in the Balmer series corresponds to the transition n = 2 → n = ∞ . Hence, n1 = 2, n2 = ∞ Balmer
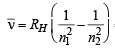
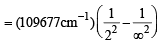
= 27419.25 cm–1
Q.13. Consider the hydrogen atom to be a proton embedded in a cavity of radius a0 (Bohr radius) whose charge is neutralised by the addition of an electron to the cavity in vacuum, infinitely slowly. Estimate the average total energy of an electron in its ground state in a hydrogen atom as the work done in the above neutralisation process. Also, if the magnitude of the average kinetic energy is half the magnitude of the average potential energy, find the average potential energy.
(1996 - 2 Marks)
Ans. Sol. Work done while bringing an electron infinitely slowly from infinity to proton of radius a0 is given as follows
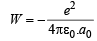
NOTE : This work done is equal to the total energy of an electron in its ground state in the hydrogen atom. At this stage, the electron is not moving and do not possess any K.E., so this total energy is equal to the potential energy.
T.E. = P. E + K. E. = P. E. = 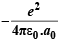 ...(1)
...(1)
In order the electron to be captured by proton to form a ground state hydrogen atom it should also attain
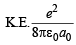
(It is given that magnitude of K.E. is half the magnitude of P.E. Note that P.E. is –ve and K.E is +ve)
∴ T.E = P. E. + K. E. 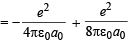
or 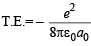
P.E. = 2 × T.E. = 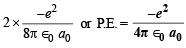
Q.14. Calculate the energy required to excite one litre of hydrogen gas at 1 atm and 298 K to the first excited state of atomic hydrogen. The energy for the dissociation of H–H bond is 436 kJ mol–1. (2000 - 4 Marks)
Ans. Sol. Determination of number of moles of hydrogen gas,
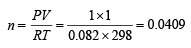
The concerned reaction is H2 —→ 2H ; ΔH = 436 kJ mol-1
Energy required to bring 0.0409 moles of hydrogen gas to atomic state = 436 × 0.0409 = 17.83 kJ
Calculation of total number of hydrogen atoms in 0.0409 mole of H2 gas 1 mole of H2 gas has 6.02 × 1023 molecules
0.0409 mole of H2 gas =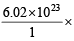 0.0409 molecules
0.0409 molecules
Since 1 molecule of H2 gas has 2 hydrogen atoms 6.02 × 1023 × 0.0409 molecules of H2 gas = 2 × 6.02 × 1023 × 0.0409 = 4.92 × 1022 atoms of hydrogen Since energy required to excite an electron from the ground state to the next excited state is given by
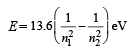
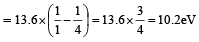
= 1.632 × 10-21 kJ
Therefore energy required to excite 4.92 × 1022 electrons
= 1.632 × 10-21 × 4.92 × 1022 kJ = 8.03 × 10 = 80.3 kJ
Therefore total energy required = 17.83 + 80.3 = 98.17 kJ
Q.15. Wavelength of high energy transition of H–atoms is 91.2nm.
Calculate the corresponding wavelength of He atoms. (2003 - 2 Marks)
Ans. Sol. For maximum energy, n1 = 1 and n2 = ∞
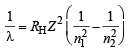
Since RH is a constant and transition remains the same
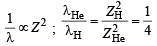
Hence, 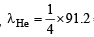 = 22.8 nm
= 22.8 nm
Q.16. The Schrodinger wave equation for hydrogen atom is (2004 - 2 Marks)
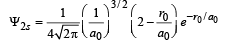
Where a0 is Bohr’s radius. If the radial node in 2s be at r0,then find r0 in terms of a0.
Ans. Sol. 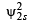 = probability of finding electron within 2s sphere
= probability of finding electron within 2s sphere
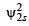 = 0 (at node)
= 0 (at node)
(∵ probability of finding an electron is zero at node)
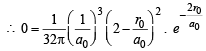
(Squaring the given value of ψ2s )
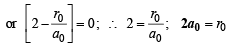
Q.17. A ball of mass 100 g is moving with 100 ms–1. Find its wavelength. (2004 - 1 Mark)
Ans. Sol. 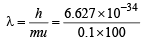
or λ = 6.627 × 10–35 m = 6.627 × 10–25Å
Q.18. Find the velocity (ms–1) of electron in first Bohr ’s orbit of radius a0. Also find the de Broglie’s wavelength (in m). Find the orbital angular momentum of 2π orbital of hydrogen atom in units of h / 2π. (2005 - 2 Marks)
Ans. Sol. For hydrogen atom, Z = 1, n = 1
v = 2.18 × 106 ×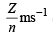 = 2. 18 × 106 ms–1
= 2. 18 × 106 ms–1
de Broglie wavelength,
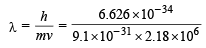
= 3.34 × 10–10 m = 3.3 Å
For 2p, l = 1
∴ Orbital angular momentum =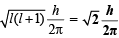
|
446 docs|930 tests
|





















