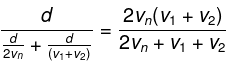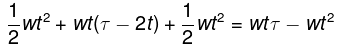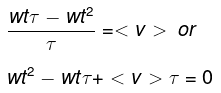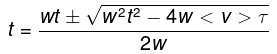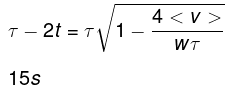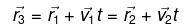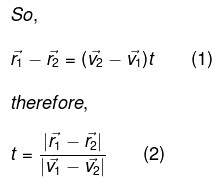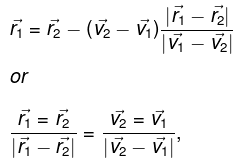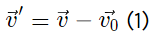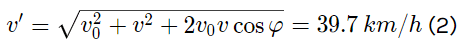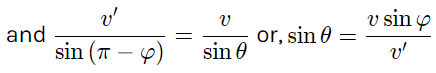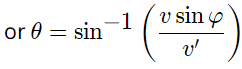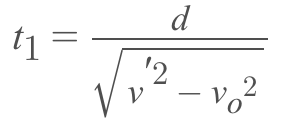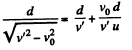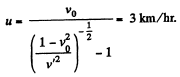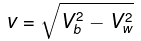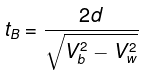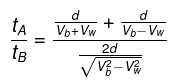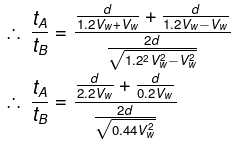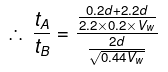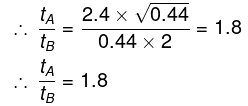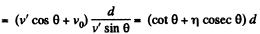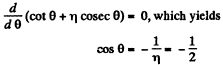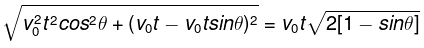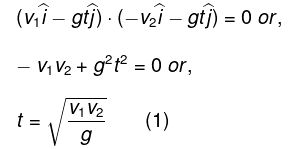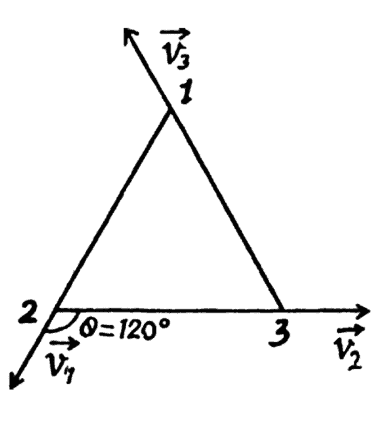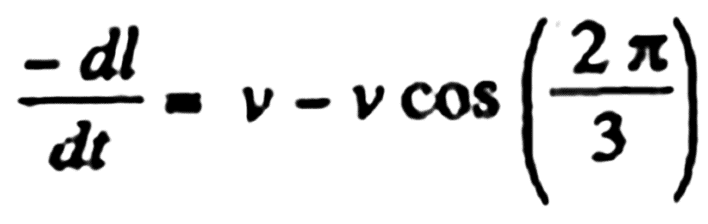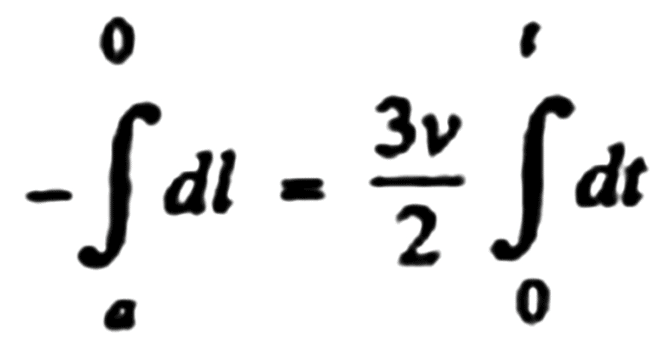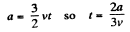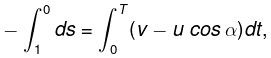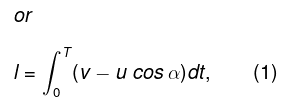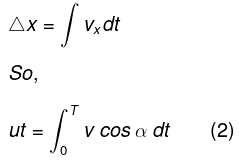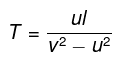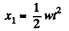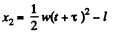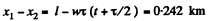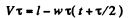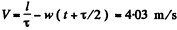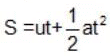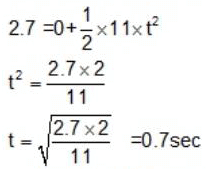Irodov Solutions: Kinematics- 1 | Physics Class 11 - NEET PDF Download
Q.1. A motorboat going downstream overcame a raft at a point A; τ = 60 min later it turned back and after some time passed the raft at a distance l = 6.0 km from the point A. Find the flow velocity assuming the duty of the engine to be constant.
There are two ways of solving this problem, i) from the point of view of an observer on the raft ii) from the point of view of a person on the ground. I will provide both these methods since, I have got a lot of questions on this problem from the readers.
Since the raft is floating on the river, it moves at the same velocity as the river. Let the velocity of the river be s. Let the velocity of the boat in still water be v. This means that the boat's downstream velocity as seen from the ground will be v+s and it upstream velocity as seen from the ground will be v-s.
- Solution From Reference Frame on the Raft
As seen by an observer on the raft, when the boat moves upstream its velocity will be v (v+s- s) and it will be -v (-v+s-s) when its moving downstream. Here, positive sign means that the boat is moving away from the raft and negative sign means that the boat is moving towards the raft.Figure 1 shows the Time-Displacement diagram of the boat and the raft as seen from the point of view of the raft. The slopes of the both upstream and downstream paths of the boat relative to the raft are vand -v. Let t1 be the time takes by the raft to meet the boat after it turns around. As seen from the figure, it is obvious that
t1 = τ (1)
Thus, thus the total time between the two meetings of the raft and the boat is
t1 + τ - 2τ (2)
Now the total distance traveled by the raft is I. This means that,
(2τ)s = I or,
s = τ / 2τ- Solution From Reference Frame on the Ground
The Time-Displacement diagram as seen from the ground of the raft and the boat are shown in Figure 2.The raft moves at a constant velocity of s downstream (the slope of the line is s) and hence its path is represented by a straight blue line in Figure 2. The boat moves at a speed v+s when going upstream, represented by a line of slope v+s in Figure 2. The boat turns around and moves at a velocity -v+s when going downstream, represented by a line of negative slope of v-s.
From Figure 2 we can see that,
(v + s)τ + (-v + s)t1 = s(t1 + τ) or,
t1 = τ(1)
Now the total distance traveled by the raft is I. This means that,
(2τ)s = I or,
s = τ / 2τ
Q.2. A point traversed half the distance with a velocity v0. The remaining part of the distance was covered with velocity v1 for half the time, and with velocity v2 for the other half of the time. Find the mean velocity of the point averaged over the whole time of motion.
Mean velocity is total distance by total time. Let the total distance traveled be d. The time taken to travel half the distance (d/2) at speed vo is d/(2vo). Now another d/2 distance remains to be traveled. Now let the time taken to travel this remaining distance be t. Then (t/2)v1 + (t/2)v2 = d/2. This means that t = d/(v1 + v2).
The total time traveled thus is, d/(2vo) + d/(v1 + v2). The total distance is d.
Thus, the mean velocity is,
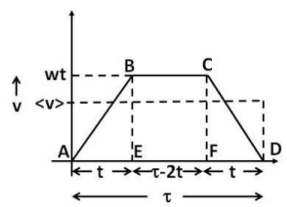
Q.3. A car starts moving rectilinearly, first with acceleration ω = 5.0 m/s2 (the initial velocity is equal to zero), then uniformly, and finally, decelerating at the same rate ω, comes to a stop. The total time of motion equals τ = 25 s. The average velocity during that time is equal to (v) = 72 km per hour. How long does the car move uniformly?
Mean velocity is total distance by total time. The v-t graph is shown in the figure beside. Suppose that time of constant acceleration was t. During the initial acceleration phase thus the car will travel 1/2wt2 and its final speed will be wt . This can also be calculated using the v-t diagram as the area under the line AB (triangle ABE).
The car will take the same time t to come to complete rest and during this deceleration phase it will travel
. This can be calculated in the v - t diagram as the area of the triangle CFD.
During the uniform motion phase the car travels at a speed wt and travels for the remaining time of τ- 2t. Thus , during the uniform motion phase i t travels a distance of wt (τ -2 t ). This can be calculated as the area of the rectangle EBCF.
The total distance traveled is thus given by,
The average velocity during the entire time is thus given by,
The above equation is a quadratic equation which has two possible solutions,
Clearly we choose the -ive sign since t cannot exceed the total time. The uniform interval is thus given by,
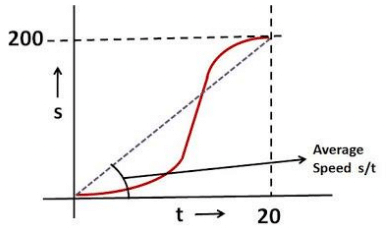
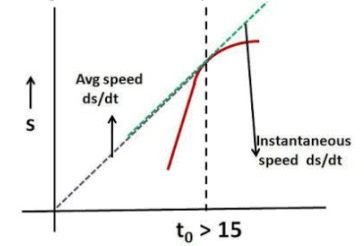
Q.4. A point moves rectilinearly in one direction. Fig. 1.1 shows the distance s traversed by the point as a function of the time t. Using the plot find:
(a) the average velocity of the point during the time of motion;
(b) the maximum velocity;
(c) the time moment t0 at which the instantaneous velocity is equal to the mean velocity averaged over the first t0 seconds.
a) The average velocity is distance traveled by time = 200cm/20sec = 10cm/sec
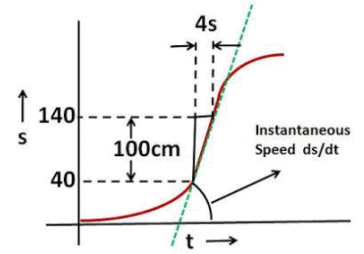
b) The maximum velocity is the point where the rate of change of distance i.e. the slope of the curve is the maximum. In the mid portion of the curve, the point moves 100cm in 4 seconds. Thus, the slope is 100/4 = 25cm/sec - this is the maximum speed achieved.
c) At any time the instantaneous speed (ds/dt) is the slope of the curve while the average speed (s/t) is the tangent of the angle of the line joining the origin to the point.
Let us first consider a time t0 during the acceleration phase of the point. This is when t0 is in the interval (0,10). Throughout this region, the slope of the curve will always be greater than that of the line joining the point to the origin since the curve is convex. This means that throughout the acceleration phase, s/t will always be less than ds/dt.
Now lets us consider the region where, the speed is constant. As shown in the picture even in this region the tangent of the line joining the point to the can never catch up the slope of the curve.
However, when we consider a time that is in the decelerating region of the curve, as the instantaneous speed of point decreases, at some time the average speed will catch up with the instantaneous speed. In other words the tangent of angle of line connecting the point to the origin will be same as the slope of the curve. This is shown in the figure beside.
Since exact nature (equation) of the curve of the decelerating part of the curve is not provided (it could be exponentially decaying) it is not possible to mathematically determine the exact value of time at which this happens. However, geometrically one can draw a tangent at every point on the curve and see if it passes through the origin. When this happens it will be the point at which instantaneous speed is same as the average speed.
Some readers have commented that this probably happens at 16s as suggested in the answer. Certainly it seems that way but the exact answer cannot be determined mathematically unless the nature of the curve is specified.
Q. 5. Two particles, 1 and 2, move with constant velocities v1 and v2. At the initial moment their radius vectors are equal to r1 and r2. How must these four vectors be interrelated for the particles to collide?
Let the particles collide at the point A (Fig.), whose position vector is
. If t be the time taken by each particle to reach at point A, from triangle law of vector addition:
From Eqs. (1) and (2)
which is the sought relationship.
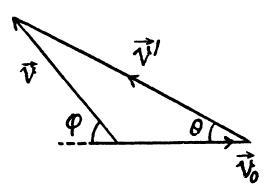
Q.6. A ship moves along the equator to the east with velocity v0 = 30 km/hour. The southeastern wind blows at an angle φ = 60° to the equator with velocity v = 15 km/hour. Find the wind velocity v' relative to the ship and the angle φ' between the equator and the wind direction in the reference frame fixed to the ship.
We have
From the vector diagram [of equation (1)] and using properties of triangle
Using (2) and putting the values of v and d
θ = 19.1o
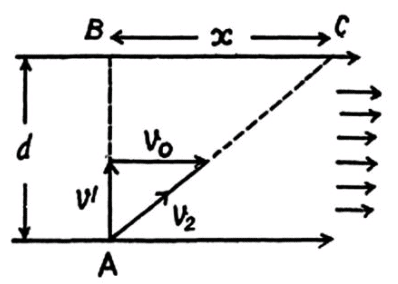
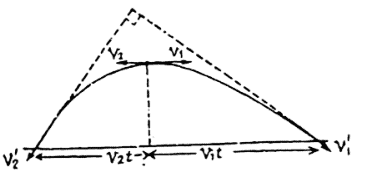
Q.7. Two swimmers leave point A on one bank of the river to reach point B lying right across on the other bank. One of them crosses the river along with the straight line AB while the other swims at right angles to the stream and then walks the distance that he has been carried away by the stream to get to point B. What was the velocity u of his walking if both swimmers reached the destination simultaneously? The stream velocity v0 = 2.0 km/hour and the velocity if of each swimmer with respect to water equals 2.5 km per hour.
Let one of the swimmer (say 1) cross the river along AB, which is obviously the shortest path. Time taken to cross the river by the swimmer 1.
(where AB = d is the width of the river).... (1)
For the other swimmer (say 2), which follows the quickest-path, the time taken to cross the river.
.... (2)
In the time t2, drifting of the swimmer 2, becomes
(3)
If t3 be the time for swimmer 2 to walk the distance x to come from C to B (Fig.), the
(4)
According to the problem t1 = t2 + 13
or
On solving we get
Q.8. Two boats, A and B, move away from a buoy anchored at the middle of a river along the mutually perpendicular straight lines: the boat A along the river, and the boat B across the river. Having moved off an equal distance from the buoy the boats returned. Find the ratio of times of motion of boats τA/τB if the velocity of each boat with respect to water is η1 = 1.2 times greater than the stream velocity.
For boat A:
Time to reach the same point back is
tA = Time upstream +time downstream
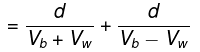
Here. vb is the speed of boat with respect to the river vw is the speed of water with respect to EarthFor boat B:
The velocity of boat is
Time to reach the same point back is
Here, vb is the speed of boat with respect to the river vw is the speed of water with respect to Earth
Hence we have the ratio as
It is also given that vb = 1.2vw
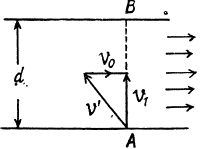
Q.9. A boat moves relative to water with a velocity which is n = 2.0 times less than the river flow velocity. At what angle to the stream direction must the boat move to minimize drifting?
Let v0 be the stream velocity and v' the velocity of boat with respect to water.
Atsome drifting of boat is inevitable.
make an angle θ with flow direction. (Fig.), then the time taken to cross the river
(where d is the width of the river)
In this time interval, the drifting of the boat
x = (v' cos θ + v0) t
For xmin (minimum drifting)
Hence, θ = 120°
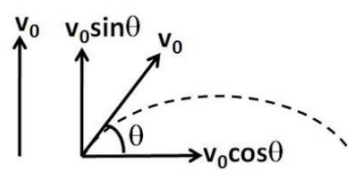
Q.10. Two bodies were thrown simultaneously from the same point: one, straight up, and the other, at an angle of θ = 60° to the horizontal. The initial velocity of each body is equal to v0 = 25 m/s. Neglecting the air drag, find the distance between the bodies t = 1.70 s later.
The figure shows the components of the velocities of the two bodies along the horizontal and vertical components. The position of the vertically thrown body after time t will be
where i and j are the unit vectors along the horizontal and vertical directions respectively. The position of the other body at a function of time will be
. Now the distance between the two is simply the Euclidean distance given by,
= 22m
Q.11. Two particles move in a uniform gravitational field with an acceleration g. At the initial moment, the particles were located at one point and moved with velocities v1 = 3.0 m/s and v2 = 4.0 m/s horizontally in opposite directions. Find the distance between the particles at the moment when their velocity vectors become mutually perpendicular.
Let us refer to the particle that was shot with v1 as P1 and the one that was shot with v2 as P2. Since v1 and v2 are supposed to be in opposite directions we arbitrarily choose v1 as the positive directions and v2 as the negative direction. Further, we assume that gravity acting downwards is the negative direction.
Since, gravity acts vertically downwards, it does not effect the horizontal components of velocities of P1 and P2. However, both P1 and P2 accelerate at equal rates of g downwards from zero initial velocity component downwards.
The velocity of P1 after time t is given by
and that of P2 is given by
When the two velocity vectors are perpendicular to each other, the dot product of the vectors will be null, i.e.
The vertical distance traveled by the P1 and P2 will be identical, thus at any time t the distance between the two particles is only a function of the horizontal components of their positions given by, (v1 + v2)t. Thus, the distance between the two particles when their velocity vectors are mutually perpendicular are given by,
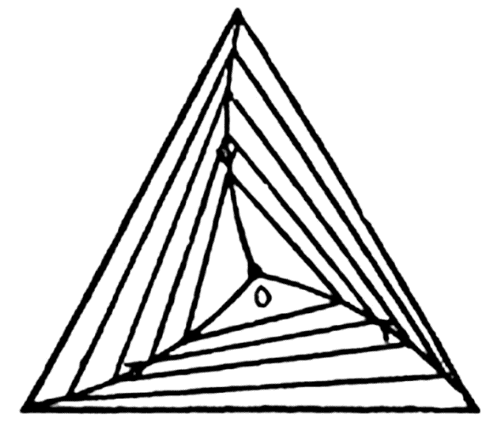
Q.12. Three points are located at the vertices of an equilateral triangle whose side equals a. They all start moving simultaneously with velocity v constant in modulus, with the first point heading continually for the second, the second for the third, and the third for the first. How soon will the points converge?
From the symmetry of the problem all the three points are always located at the vertices of equilateral triangles of varying side length and finally meet at the centriod of the initial equilateral triangle whose side length is a, in the sought time interval (say t ).
Let us consider an arbitrary equilateral triangle of edge length l (say).
Then the rate by which 1 approaches 2, 2 approaches 3, and 3 approaches 1, becomes:
On integrating
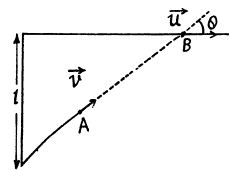
Q.13. Point A moves uniformly with velocity v so that the vector v is continually "aimed" at point B which in its turn moves rectilinearly and uniformly with velocity u< v. At the initial moment of time v ⊥ u and the points are separated by a distance 1. How soon will the points converge?
Let us locate points A and B at an arbitrary instant of time (Fig.).
If A and B are separated by the distance s at this moment, then the points converge or point A approaches B with velocity -ds/dt = v - ucosα where angle α varies with time.On integrating,
(where T is the sought time)
As both A and B cover the same distance in jc-direction during the sought time interval, so the other condition which is required can be obtained by the equation
Solving (1) and (2), we get
One can see that if w = v, or u < v, point A cannot catch B.
Q.14. A train of length l = 350 m starts moving rectilinearly with constant acceleration w = 3.0.10-2 m/s2; t = 30 s after the start the locomotive headlight is switched on (event 1), and τ = 60 s after that event the tail signal light is switched on (event 2). Find the distance between these events in the reference frames fixed to the train and to the Earth. How and at what constant velocity V relative to the Earth must a certain reference frame K move for the two events to occur in it at the same point?
In the reference frame fixed to the train, the distance between the two events is obviously equal to l. Suppose the train starts moving at time t = 0 in the positive x direction and take the origin (x = 0) at the head-light o f the train at t = 0. Then the coordinate o f first event in the earth’s frame is
and similarly the coordinate of the second event is
The distance between the two events is obviously.
in the reference frame fixed on the earth..
For the two events to occur at the same point in the reference frame K, moving with constant velocity V relative to the earth, the distance travelled by the frame in the time interval T must be equal to the above distance.
Thus
So,
The frame K must clearly be moving in a direction opposite to the train so that if (for example) the origin of the frame coincides with the point x1 on the earth at time t, it coincides with the point x2 at time t + τ.
Q. 15. An elevator car whose floor-to-ceiling distance is equal to 2.7 m starts
ascending with constant acceleration 1.2 m/s2; 2.0 s after the start a bolt begins falling from the ceiling of the car.
Find:
(a) the bolt's free fall time.
(b) the displacement and the distance covered by the bolt during the free fall in the reference frame fixed to the elevator shaft.
(a) Given that:
(i) Distance between the elevator floor and ceiling, S = 2.7 m
(ii) Acceleration of the elevator, a = 1.2 m/s2
⇒ Relative to the elevator the acceleration of the bolt = (g + a) = (9.8 + 1.2) = 11 m/s2
Let 't' be the time taken by the bolt to reach the floor of the elevator of height 2.7 m.
At the moment bolt starts to fall, Relative to the elevator the velocity of the bolt = 0
From the equation of motion,
∵ S = 2.7 m, a = 11 m/s2, u = 0
On substituting we get that:
Thus, free fall time of the bolt = 0.7 sec(b) Displacement:
Let 0 be the position of the elevator ceiling when the bolt starts to fall. The elevator floor at this time is at -2.7 m. The upward velocity of the elevator at this point is 1.2 x 2 = 2.4 m/s. After 0.7 seconds the position of the elevator will be at -2.7 + 2.4(0.7) + 1 2 (1.2) (0.7)2 = -0.726 m.
Since the bolt essentially traveled from ceiling to floor, its final displacement was same as the position of the floor. Thus, the bolt displaced about 0.7 m.
Distance:The reason distance is different from displacement is because the bolt will first travel upwards before it starts to descend. Distance calculation must hence include the length of the entire path followed by the bolt. The bolt will travel for 2.4/9.8 = 0.243 sec and is at a height of 2.4 x (0.243) - 1/2(9.87)(0.243)2 = 0.292 m from the point it detached from the elevator before it begins to descend towards the elevator floor. For the rest of the time 0.7-0.243 = 0.457 sec the bolt free falls starting at 0 velocity.
The distance traveled during this time is given by, 1/2(9.87)(0.457)2 = 1.03m.
The total distance traveled by the bolt is thus given by 0.292 + 1.03 = 1.322 m.
|
95 videos|367 docs|98 tests
|
FAQs on Irodov Solutions: Kinematics- 1 - Physics Class 11 - NEET
| 1. What is Kinematics? |  |
| 2. What are the three types of motion in Kinematics? |  |
| 3. What is the difference between speed and velocity in Kinematics? |  |
| 4. What is the formula for acceleration in Kinematics? |  |
| 5. What is projectile motion in Kinematics? |  |