Fluid Kinematics | Fluid Mechanics for Civil Engineering - Civil Engineering (CE) PDF Download
| Table of contents |

|
| Introduction |

|
| Main AspectsThe subject has three main aspects: |

|
| Scalar & Vector Fields |

|
| Description of Fluid Motion(a) Lagrangian Method |

|
Introduction
Kinematics is the geometry of motion. Kinematics of fluid describes the fluid motion and its consequences without consideration of the nature of forces causing the motion.Main Aspects
The subject has three main aspects:- Development of methods and techniques for describing and specifying the motions of fluids.
- Determination of the conditions for the kinematic possibility of fluid motions.
- Characterization of different types of motion and associated deformation rates of any fluid element.
 |
Test: Types of Fluid Flow
|
Start Test |
Scalar & Vector Fields
➢ Scalar: Scalar is a quantity that can be expressed by a single number representing its magnitude.
Example: Mass, Density, and Temperature.
➢ Scalar Field: If at every point in a region, a scalar function has a defined value, the region is called a scalar field.
Example: Temperature distribution in a rod.
➢ Vector: Vector is a quantity that is specified by both magnitude and direction.
Example: Force, Velocity, and Displacement.
➢ Vector Field: If at every point in a region, a vector function has a defined value, the region is called a vector field.
Example: Velocity field of a flowing fluid.
➢ Flow Field: The region in which the flow parameters i.e. velocity, pressure, etc. are defined at each and every point at any instant of time is called a flow field. Thus, a flow field would be specified by the velocities at different points in the region at different times.
Description of Fluid Motion
(a) Lagrangian Method
Using the Lagrangian method, the fluid motion is described by tracing the kinematic behavior of each particle constituting the flow.
Identities of the particles are made by specifying their initial position (spatial location) at a given time. The position of a particle at any other instant of time then becomes a function of its identity and time.
➢ Analytical expression of the last statement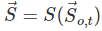
where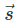 is the position vector of a particle (with respect to a fixed point of reference) at a time t. (6.1)
is the position vector of a particle (with respect to a fixed point of reference) at a time t. (6.1)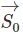 is its initial position at a given time, t =t0
is its initial position at a given time, t =t0
Equation (6.1) can be written into scalar components with respect to a rectangular cartesian frame of coordinates as:
► x = x(x0,y0,z0,t) (6.1a)
► y = y(x0,y0,z0,t) (6.1b)
► z = z(x0,y0,z0,t) (6.1c)
where, x0,y0,z0 are the initial coordinates and x, y, z are the coordinates at a time t of the particle.
Hence can be expressed as:
can be expressed as:
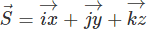 |  are the unit vectors along x, y and z axes respectively. are the unit vectors along x, y and z axes respectively. |
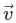 and acceleration of the fluid particle can be obtained from the material derivatives of the position of the particle with respect to time.
and acceleration of the fluid particle can be obtained from the material derivatives of the position of the particle with respect to time.Therefore,
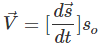 (6.2a)
(6.2a)In terms of scalar components: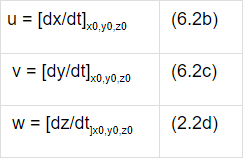
where u, v, w are the components of velocity in x, y, z directions respectively.
Similarly, for the acceleration, 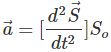 (6.3a)and hence,
(6.3a)and hence,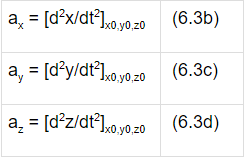
where ax, ay, az are accelerations in x, y, z directions respectively.
➢ Advantages of Lagrangian Method
- Since the motion and trajectory of each fluid particle are known, its history can be traced.
- Since particles are identified at the start and traced throughout their motion, conservation of mass is inherent.
➢ Disadvantages of Lagrangian Method
- The solution of the equations presents appreciable mathematical difficulties except for certain special cases and therefore, the method is rarely suitable for practical applications.
(b) Eulerian Method
- The method was developed by Leonhard Euler.
- This method is of a greater advantage since it avoids the determination of the movement of each individual fluid particle in all details.
- It seeks the velocity
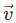 and its variation with time t at each and every location
and its variation with time t at each and every location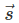 in of the flow field.
in of the flow field. - In the Eulerian view, all hydrodynamic parameters are functions of location and time.
➢ Mathematical representation of the flow field in the Eulerian method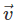 = v (
= v (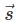 , t) (6.4), where
, t) (6.4), where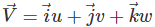 and
and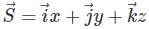 Therefore:
Therefore:
► u = u (x, y, z, t)
► v = v (x, y, z, t)
► w = w (x, y, z, t)
(c) The Relation Between Eulerian & Lagrangian Method
The Eulerian description can be written as: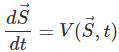 (6.5)
(6.5)
or
dx/dt = u(x,y,z,t)
dy/dt = v(x,y,z,t)
dz/dt = w(x,y,z,t)
The integration of Eq. (6.5) yields the constants of integration which are to be found from the initial coordinates of the fluid particles.
Hence, the solution of Eq. (6.5) gives the equations of Lagrange as: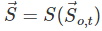 or x = x(x0,y0,z0,t)
or x = x(x0,y0,z0,t)
y = y(x0,y0,z0,t)
z = z(x0,y0,z0,t)
The above relation is the same as the Lagrangian formulation.
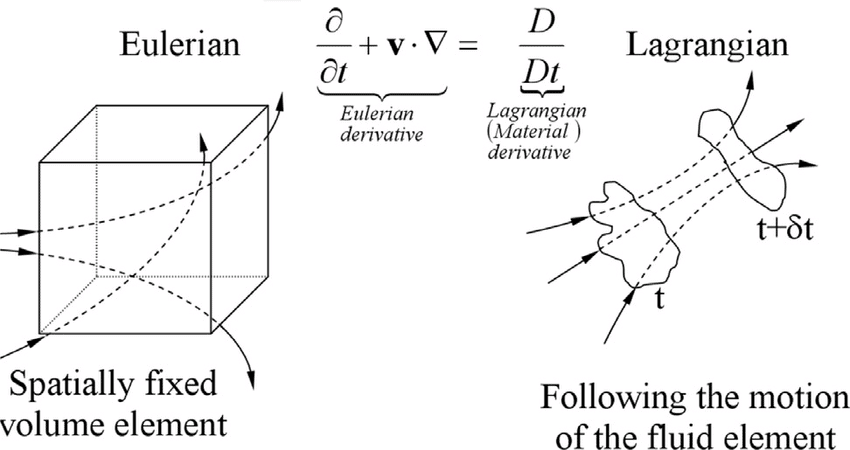 In principle, the Lagrangian method of description can always be derived from the Eulerian method.
In principle, the Lagrangian method of description can always be derived from the Eulerian method.
|
54 videos|97 docs|110 tests
|
FAQs on Fluid Kinematics - Fluid Mechanics for Civil Engineering - Civil Engineering (CE)
| 1. What is the difference between scalar and vector fields in fluid mechanics? |  |
| 2. How can the Lagrangian method be used to study fluid motion? |  |
| 3. What is fluid kinematics in civil engineering? |  |
| 4. What are some applications of fluid kinematics in civil engineering? |  |
| 5. Can you provide an example of a scalar field in fluid mechanics? |  |