Ligand Substitution Mechanisms | Chemistry Optional Notes for UPSC PDF Download
| Table of contents |

|
| Ligand Substitution Reactions |

|
| Associative Substitution |

|
| Dissociative Substitution |

|
| Interchange Substitution |

|
Ligand Substitution Reactions
- Ligand substitution is one of the simplest reactions a metal complex may undergo. In general, ligand substitution involves the exchange of one ligand for another, with no change in oxidation state at the metal center. The incoming and outgoing ligands may be neutral or ionic but the charge of the complex changes if the ligand charge changes. Keep charge conservation in mind when writing out ligand substitutions.
- How do we know when a ligand substitution reaction is favorable? The thermodynamics of the reaction depend on the relative strength of the two metal-ligand bonds, and the stability of the departing and incoming ligands (or salts of the ligand, if they’re ionic). It’s often useful to think of X-for-X substitutions like acid-base reactions, with the metal and spectator ligands serving as a “glorified proton.”
- Like acid-base equilibria in organic chemistry, we look to the relative stability of the two charged species (the free ligands) to draw conclusions. Of course, we don’t necessarily need to rely just on thermodynamics to drive ligand substitution reactions. Photochemistry, neighboring-group participation, relative concentrations, and other tools can facilitate otherwise difficult substitutions.
- Ligand substitution is characterized by a continuum of mechanisms bound by associative (A) and dissociative (D) extremes. At the associative extreme, the incoming ligand first forms a bond to the metal, then the departing ligand takes its lone pair and leaves. At the dissociative extreme, the order of events is opposite—the departing ligand leaves, then the incoming ligand comes in.
- Associative substitution is common for square planar (like d8 complexes of Ni, Pd, and Pt), while dissociative substitution is more common for octahedral complexes. Then again, reality is often more complicated than these extremes. In some cases, evidence is available for simultaneous dissociation and association, and this mechanism has been given the name interchange (IA or ID).
Associative Substitution
- The associative substitution reaction is the inorganic analog of an SN2 reaction. In associative ligand substitution, the incoming ligand (Y) forms a new bond with the metal (M) before the bond to the leaving ligand (X) breaks. The first step, formation of the new M-Y bond is generally rate-determining. A typical mechanism for associative ligand substitution in both octahedral and square planar complexes is shown in Figure 10.3.1.

- In an octahedral complex the intermediate is 7 coordinate, so associative ligand exchange in octahedral complexes is rare and only favored with larger metal ions and ligands that are not sterically demanding. In contrast, ligand substitution in square planar complexes almost always occurs via an associative mechanism, involving approach of the incoming ligand to the open coordination sites above or below the plane. Let’s begin with the kinetics of the reaction. How can we spot an associative mechanism in experimental data, and what are some of the consequences of this mechanism?

Figure 10.3.1: Scheme of associative ligand substitution in an octahedral (top) and square planar (bottom) metal complex.
Reaction Kinetics

Reaction kinetics are commonly used to elucidate reaction mechanisms, and ligand substitution is no exception. Different mechanisms of substitution may follow different rate laws, so plotting the dependence of reaction rate on concentration often allows us to distinguish mechanisms. In the associative mechanism, the rate law is second order overall, first order in both LnMX and Y. (Figure 10.3.2). If a large excess of Y is used in the reaction is will become pseudo first order, where the reaction appears first order because the [Y] doesn't change significantly over the course of the reaction. Figure 10.3.2: Dependence of associative reaction rate on concentration of the starting metal complex [MLnX] and the incoming ligand [Y].
Figure 10.3.2: Dependence of associative reaction rate on concentration of the starting metal complex [MLnX] and the incoming ligand [Y].
Dissociative Substitution
- The associative substitution mechanism is unlikely for 6 coordinate complexes. For octahedral complexes dissociative substitution mechanisms involving 5 coordinate intermediates are more likely. In a slow step, the departing ligand leaves, generating a coordinatively unsaturated 5 coordinate intermediate. The incoming ligand then enters the coordination sphere of the metal to generate the product.
- We’ll focus on the kinetics of the reaction and the nature of the unsaturated intermediate (which influences the stereochemistry of the reaction). The reverse of the first step, re-coordination of the departing ligand (rate constant k–1), is often competitive with dissociation.


Figure 10.3.3: A general scheme for dissociative ligand substitution in an octahedral complex.
Reaction Kinetics
Let’s begin with the general situation in which k1 and k–1 are similar in magnitude. Since k1 is rate limiting, k2, the rate of the second step is assumed to be much larger than k1 and k–1. Most importantly, we need to assume that variation in the concentration of the unsaturated intermediate is essentially zero. This is called the steady state approximation, and it allows us to set up an equation that relates reaction rate to observable concentrations.
Of course, the unsaturated complex is present in very small concentration and is unmeasurable, so this equation doesn’t help us much. We need to remove the concentration of the unmeasurable intermediate from (1), and the steady state approximation helps us do this. We can express variation in the concentration of the unsaturated intermediate as (processes that make it) minus (processes that destroy it), multiplying by an arbitrary time length to make the units work out. All of that equals zero, according to the steady state approximation.
Rearranging to solve for [L_nM], we arrive at the following.
Finally, substituting into Equation 10.3.5 we reach a verifiable rate equation.
When k–1 is negligibly small, Equation 10.3.9 reduces to the familiar Equation 10.3.10, typical of dissociative reactions like SN1.
This rate does not depend on the concentration of incoming ligand. For reactions that are better described by Equation 10.3.9, we can use a large excess of Y to make k2[Y] far greater than k−1[X], essentially forcing the reaction to fit Equation 10.3.10.
Figure 10.3.4: Dependence of dissociative reaction rate on concentration of the starting metal complex [MLnX] and the incoming ligand [Y].
Stereochemistry
- Dissociation of a ligand from an octahedral complex generates an unsaturated ML5 intermediate. The five coordinate intermediate could adopt either a trigonal bipyramidal (TBP) geometry or a square pyramidal geometry (SP). Both steric and electronic factors combine to determine which geometry is most favorable. For example, with 6 d electrons an issue arises with the TBP geometry.
- With 6 d electrons, the TBP geometry has two unpaired electrons in degenerate orbitals. Unpaired electrons in degenerate orbitals lead to Jahn-Teller distortion. For a TBP geometry, distortion to a SP or a distorted TBP geometry removes the degeneracy, and so five-coordinate d6 complexes typically have square pyramidal or distorted TBP geometries.
 Figure 10.3.5: TBP geometry (left) is electronically disfavored for d6 metals. Distorted TBP (right) and SP (center) geometries are favored.
Figure 10.3.5: TBP geometry (left) is electronically disfavored for d6 metals. Distorted TBP (right) and SP (center) geometries are favored. - When the intermediate adopts square pyramidal geometry, the incoming ligand can simply approach where the departing ligand left, resulting in retention of stereochemistry. Inversion is more likely when the intermediate is a distorted trigonal bipyramid.
Factors That Favor Dissociative Substitution
- In general, introducing structural features that either stabilize the unsaturated intermediate or destabilize the starting complex can encourage dissociative substitution. Both of these strategies lower the activation barrier for the reaction.
- Let’s begin with features that stabilize the unsaturated intermediate. Electronically, the intermediate loves it when its d electron count is nicely matched to its crystal field orbitals. As you study inorganic chemistry, you’ll learn that there are certain “natural” d electron counts for particular geometries that fit well with the metal-centered orbitals predicted by crystal field theory. Octahedral geometry is great for six d electrons, for example, and square planar geometry loves eight d electrons.
- Complexes with “natural” d electron counts—but bearing one extra ligand—are ripe for dissociative substitution. The classic examples are d8 TBP complexes, which become d8 square planar complexes (think Pt(II) and Pd(II)) upon dissociation. Similar factors actually can also stabilize the starting complexes, making them less reactive in dissociative substitution reactions. Fro example, low spin d6 octahedral complexes are particularly happy, and react most slowly in dissociative substitutions.
- Destabilization of the starting complex is commonly accomplished by adding steric bulk to its ligands. Naturally, dissociation relieves steric congestion in the starting complex. Chelation has the opposite effect, and tends to steel the starting complex against dissociation.

Interchange Substitution
Real life chemical reactions don't always fall neatly into one of the categories above. In some cases the M-X bond can break and the M-Y bond can form simultaneously. An interchange reaction is a concerted reaction without an intermediate. The transition state is a species where the bond to Y is partially formed and the bond to X is partially broken as seen in Figure 10.3.6. If the new M-Y bond forms faster than the M-X bond breaks tat is an associative interchange (IA) reaction and if the M-X bond breaks faster than the new M-Y bond forms that is a dissociative interchange reaction (ID)
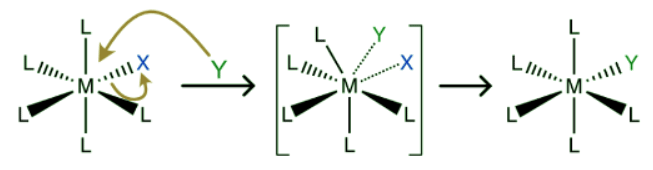
Figure 10.3.6: A general scheme for an interchange ligand substitution reaction. Species in brackets is the transition state, not an intermediate.
FAQs on Ligand Substitution Mechanisms - Chemistry Optional Notes for UPSC
| 1. What are ligand substitution reactions? |  |
| 2. What is associative substitution in ligand substitution reactions? |  |
| 3. What is dissociative substitution in ligand substitution reactions? |  |
| 4. What is interchange substitution in ligand substitution reactions? |  |
| 5. What are some examples of ligand substitution reactions? |  |

|
Explore Courses for UPSC exam
|

|




 Figure 10.3.5: TBP geometry (left) is electronically disfavored for d6 metals. Distorted TBP (right) and SP (center) geometries are favored.
Figure 10.3.5: TBP geometry (left) is electronically disfavored for d6 metals. Distorted TBP (right) and SP (center) geometries are favored.
















