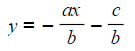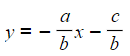Class 10 Exam > Class 10 Notes > Mathematics for GCSE/IGCSE > Linear Graphs
Linear Graphs | Mathematics for GCSE/IGCSE - Class 10 PDF Download
Finding Equations of Straight Lines
Why do we want to know about straight lines and their equations?
- Straight Line Graphs (Linear Graphs) have numerous applications in mathematics, such as in navigation.
- We might need to determine the equation of a straight line to program it into a computer. This computer can then plot the line on a screen, alongside other lines, to create shapes and graphics.
How do we find the equation of a straight line?
- The equation of a straight line is defined by the formula: (y = mx + c)
- Here, ( m ) represents the gradient, and ( c ) is the y-axis intercept (or simply, the y-intercept)
- To determine the equation of a straight line, you need two essential pieces of information:
- Obtain the gradient, ( m), directly from the question or calculate it using
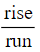 or gradient formula or two given points
or gradient formula or two given points - Choose any point on the line and substitute its coordinates into y = mx + c (as you already know both ( m ) and the point)
- Solve to find the value of ( c ) if you are given two points that were used to determine the gradient
- Obtain the gradient, ( m), directly from the question or calculate it using
- If ( m ) is a fraction, you may be required to present the equation in a suitable form ax + by + c = 0
- When in doubt, sketch the line to visually represent the problem
What if the line is not in the form y = mx + c?
- A line could be given in the form ax + by + c = 0
- It is harder to identify the gradient and intercept in this form
- We can rearrange the equation into y = mx + c, so it is easier to identify the gradient and intercept
- ax + by + c = 0
- Subtract ax from both sides
- by + c = - ax
- Subtract c from both sides
- by = - ax - c
- Divide both sides by b
- In this case, the gradient is
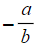 and the y-intercept is
and the y-intercept is 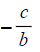
Drawing Linear Graphs
Drawing Linear Graphs: Understanding the Basics
- Before attempting to sketch a straight line, it's crucial to grasp how to derive the equation of a straight line. This understanding is fundamental to drawing accurate graphs.
- The method of drawing a straight line varies based on the form in which the equation is presented. The two primary forms are y = mx + c and ax + by = c.
Different Approaches to Drawing Linear Graphs
- When the equation is in the form y = mx + c, where 'm' is the slope and 'c' is the y-intercept, follow these steps:
- Locate 'c' on the y-axis.
- Move 1 unit to the right and 'm' units upwards (repeat this process to plot more points on the line).
- For the equation ax + by = c, you can identify the intercepts by:
- Setting x = 0 to find the y-axis intercept.
- Setting y = 0 to find the x-axis intercept.
(Alternatively, you may rearrange the equation to y = mx + c and apply the previous method.)
The document Linear Graphs | Mathematics for GCSE/IGCSE - Class 10 is a part of the Class 10 Course Mathematics for GCSE/IGCSE.
All you need of Class 10 at this link: Class 10
|
38 videos|395 docs|19 tests
|
FAQs on Linear Graphs - Mathematics for GCSE/IGCSE - Class 10
| 1. What is the general equation of a straight line in mathematics? |  |
Ans. The general equation of a straight line is y = mx + c, where m represents the gradient of the line and c represents the y-intercept.
| 2. How do you find the equation of a straight line given two points on the line? |  |
Ans. To find the equation of a straight line given two points (x1, y1) and (x2, y2) on the line, you can first calculate the gradient using the formula m = (y2 - y1) / (x2 - x1), and then substitute the gradient and one of the points into the general equation y = mx + c to find the y-intercept c.
| 3. How do you interpret the gradient of a straight line on a graph? |  |
Ans. The gradient of a straight line on a graph represents the rate of change of y with respect to x. A positive gradient indicates an increasing relationship between x and y, while a negative gradient indicates a decreasing relationship.
| 4. How can you determine if two straight lines are parallel or perpendicular? |  |
Ans. Two straight lines are parallel if they have the same gradient, and they are perpendicular if the product of their gradients is -1.
| 5. How can you use the equation of a straight line to determine the y-value for a given x-value? |  |
Ans. To determine the y-value for a given x-value using the equation of a straight line, you can substitute the x-value into the equation y = mx + c and solve for y.
Related Searches