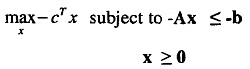Linear Programming: Problem Formulation | Management Optional Notes for UPSC PDF Download
Formulation: Structure and Variables of Linear Programming
We can represent a real-world problem using Linear Programming (LP). Take for instance the following scenario:
Example 1: Dietary Dilemma
A doctor aims to design the most cost-effective diet that fulfills the nutritional needs of her patients. The patients necessitate 4, 8, and 9 units of nutrition A, B, and C per week, respectively. There are four types of food options available, each with its own nutritional content per kilogram, as detailed in the table below.
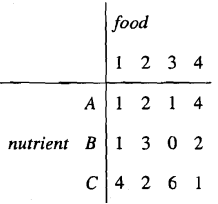
If the food is priced at Rs. 5, 7, 7, and 9 per kilogram respectively, we need to determine the optimal weekly diet for the patients, focusing on meeting the nutritional requirements, particularly for nutrient B. To achieve this, we must address the following linear programming problem:
If we allocate xj units of food type j, the objective is to solve the following linear programming problem.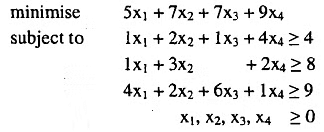
We can write this in matrix form as

Please note that
- minimizing cTx is the same as maximizing -cTx.
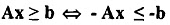
Therefore, we write the problem
Example 2: A manufacturer operates two types of machines. To maintain production standards, a minimum of three A-type machines and one B-type machine are required. The production cost for each A-type machine is Rs. 1000, while for each B-type machine, it's Rs. 1200. Additionally, the floor space occupied by these machines is 4m² and 5m² respectively. The total production cost cannot exceed Rs. 15000, and the available floor space is limited to 40m².
- Let x and y represent the number of A-type and B-type machines respectively. The production cost constraint can be expressed as 1000x + 1200y ≤ 15000, and this formulation implies the constraint 5x + 6y ≤ 75 for space.
- Considering the space constraint, we have 4x + 5y ≤ 40. Furthermore, for the A-type machines, we have the constraint x ≥ 3, and for the B-type machines, x ≥ 1.
Assuming the weekly profit is Rs. 120 for each A-type machine and Rs. 100 for each B-type machine, the objective is to determine the combination of machine usage that yields maximum profit. If the total profit, denoted as p, is calculated as 120x + 100y, then the problem is to optimize the objective function p = 120x + 100y subject to constraints (1), (2), (3), and (4) outlined above. Here, x and y represent decision variables.