Magnification & Power of a Lens | Science Class 10 PDF Download
Lenses
- A lens is a piece of any transparent material bounded by two curved surfaces or by one curved and one plane surface.
- Lens are of two types:
Convex or convergent lens Concave or divergent lens
Concave or divergent lens
Terminologies
- Optical Centre: O is a point for a given lens through which any ray passes undeviated.
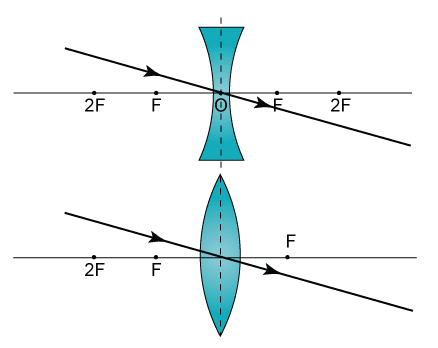
- Principal Axis: C1C2 is a line passing through optical centre and perpendicular to the lens.
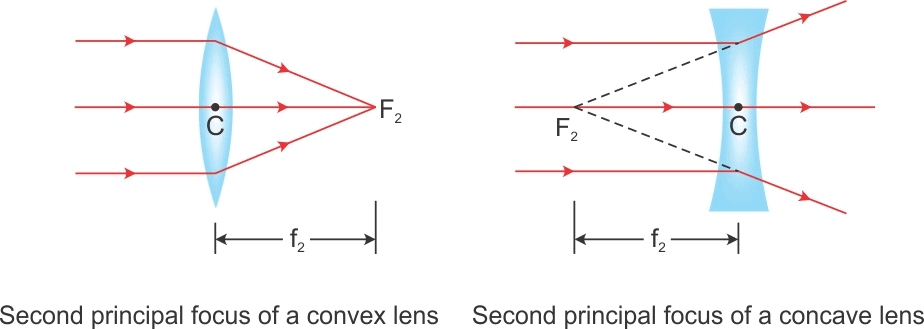
- Principal Focus: A lens has two surfaces and hence two focal points. First focal point is an object point on the principal axis for which image is formed at infinity.
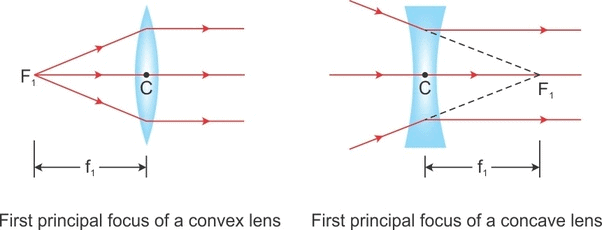
- While second focal point is an image point on the principal axis for which object lies at infinity.
- Focal Length f is defined as the distance between optical centre of a lens and the point where the parallel beam of light converges or appears to converge.
- Aperture : In reference to a lens, aperture means the effective diameter. Intensity of image formed by a lens which depends on the light passing through the lens will depend on the square of aperture, i.e., I µ (Aperture)2
Rules for Image Formation
- A ray passing through optical centre proceeds undeviated through the lens.
- A ray passing through first focus or directed towards it, after refraction from the lens, becomes parallel to the principal axis.
- A ray passing parallel to the principal axis after refraction through the lenses passes or appears to pass through F2.
For Convergent or Convex Lens:
| Object | Image | Magnification |
| ∞ | F | m << – 1 |
| ∞ – 2F | F – 2F | m < –1 |
| 2F | 2F | m = –1 |
| F – 2F | ∞ – 2F | m > –1 |
| F | ∞ | m >> –1 |
| F – O | In front of lens | m > + 1 |
Image Formation for Convex Lens
- Object is placed at infinity.
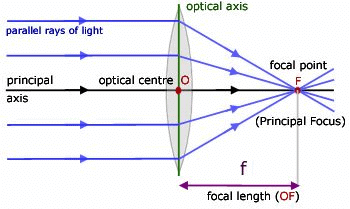 Image: at F real, inverted, very small in size and m << - 1
Image: at F real, inverted, very small in size and m << - 1 - Object is placed in between ∞ -2F.
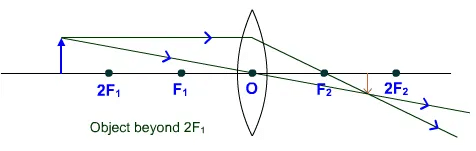
Image: real (F - 2F) inverted, small in size (diminished), and m < - 1 - Object is placed at 2F.
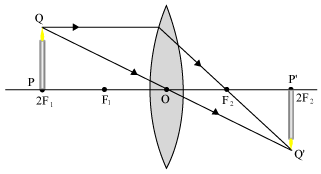 Image : real (at 2F)
Image : real (at 2F)
inverted
equal (of same size)
(m = -1) - Object is placed in between 2F - F.
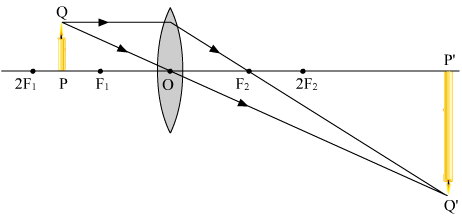 Image : real (2F - ∞)
Image : real (2F - ∞)
inverted
enlarged
m > 1 - Object is placed at F.
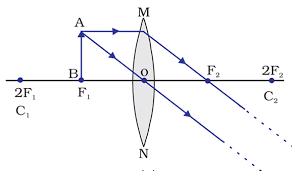
- Object is placed in between F - O.
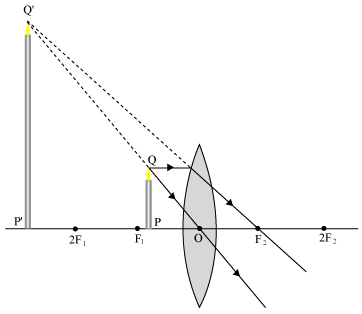 Image: virtual (in front of lens)
Image: virtual (in front of lens)
erected
enlarge
(m > + 1)
| Given | Real | Virtual |
| u | - | - |
| v | + | - |
| h1 | + | + |
| h2 | - | + |
| m | - | + |
Image Formation for Concave Lens
Image is virtual, diminished, erect, towards the object, m = +ve
- Object is placed at infinity.
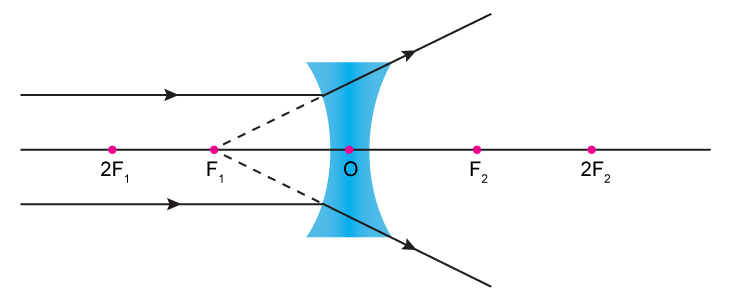 Image: At F
Image: At F
virtual
erected
diminished
(m << + 1) - Object is placed in front of the lens.
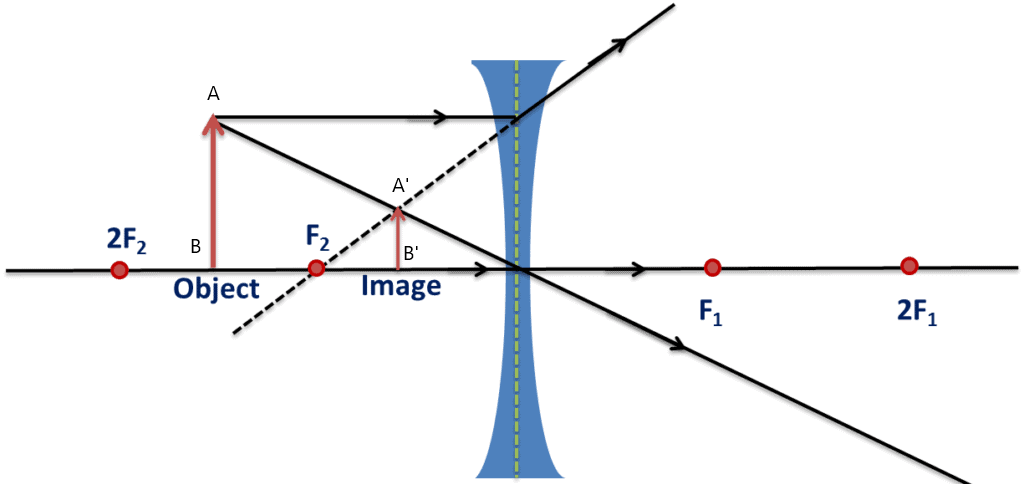 Image: between F and optical centre
Image: between F and optical centre
virtual
erected
diminished
(m < + 1)
Lens Formula
Focal length of a lens can be found by the following formula:
Where - f = Focal length of lens.
v = Distance of image from pole
u = Distance of object from pole.
Uses of Lens Formula
(i) Put the correct signs of known variables according to the sign conventions.
(ii) Do not put the sign of an unknown variable. The sign will automatically show up during calculations.
(iii) If the calculated sign of a variable turns out positive, then the variable calculated is on the other side of the lens, i.e., on the opposite side to the object. However, if the calculated variable is of negative sign, then it is on the same side as the object.
Combination of lenses
Two thin lens are placed in contact to each other
Power of combination:
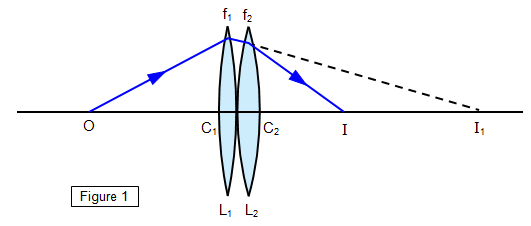 P = P1 + P2
P = P1 + P2
1/F = 1/f1 + 1/f2
Use sign convention when solving numericals.
Two thin lenses are placed at a small distance a.
 1/F = 1/f1 + 1/f2 - a/f1f2
1/F = 1/f1 + 1/f2 - a/f1f2
P = P1 + P2 - a P1P2
Use sign convention when solving numericals.
Power of Lens
The power of a lens is defined as the reciprocal of focal length of the lens. Focal length should always be measured in meters.
Unit of power of lens is 1/meter which is called dioptre.
Magnification of Lens
The magnification is defined as the ratio of the height of the image and the height of the object it is represented by M.
Uses of Lenses in Daily Life
Lenses are using is microscope, telescope. prism, binoculars and slide projector etc.
Relation between focal length (f) and Radius of curvature (R):
Focal length of a lens depends on following factors:
- Refractive index of the material of the lens.
- Radius of curvature R1 and R2 of both in curved surfaces of the lens.
- Colour (wave length) of the light.
Formula of making a spherical lens of specific focal length.
Where f is the average value of focal length for all the colours. µ is the refractive index of the material of the lens with respect to air. R1 and R2 are the radius of curvature of the curved surfaces respectively. R1 is positive and R2 is negative for convex lens. R1 is negative and R2 positive for concave lens.
|
80 videos|569 docs|80 tests
|






















