Mathematics Olympiad Model Test Papers - 1 | Olympiad Preparation for Class 10 PDF Download
| Table of contents |

|
| Logical Reasoning |

|
| Mathematical Reasoning |

|
| Everyday Mathematics |

|
| Achievers Section |

|
Note: The questions provided in this document are similar to the questions that were asked in the actual Olympiad exam. So, we recommend you study these for your Olympiad preparation
Logical Reasoning
Q1: The next term of the sequence 4, 9, 21, 47, 101, 211, … is
(a) 421
(b) 433
(c) 427
(d) 441
 View Answer
View Answer 
Ans: (b)
Each number is doubled and 1, 3, 5, 7, 9, … respectively are added.
Q2: In the provided letter sequence, certain letters are absent and are listed in the options below. Choose the correct option.
(a) baaa
(b) bacb
(c) abca
(d) abba
 View Answer
View Answer 
Ans: (b)
- The sequence has missing letters that need to be filled in to maintain a logical pattern.
- By analyzing the sequence, the correct letters that fit the pattern are found in option (b) ""bacb"".
- This option completes the series correctly, ensuring the letters follow the established order.
- Other options do not fit the sequence as well as option (b) does.
Q3: Arrange the following words in a logical sequence: Neck, Head, Nose, Feet, Stomach
(a) 2, 1, 3, 5, 4
(b) 3, 1, 2, 4, 5
(c) 5, 4, 2, 1, 3
(d) 2, 3, 1, 5, 4
 View Answer
View Answer 
Ans: (d)
- The correct order starts from the top of the body and moves downwards.
- Head (2) is at the top, followed by Nose (3), then Neck (1), followed by Stomach (5), and finally Feet (4) at the bottom.
- This sequence reflects the anatomical structure of the human body.
- Thus, the logical arrangement is 2, 3, 1, 5, 4.
Q4: Choose the number-letter group which is different from the others.
(a) M5S
(b) B9L
(c) T4Y
(d) F4J
 View Answer
View Answer 
Ans: (d)
In the given options, each group follows a pattern in terms of the difference between the positions of the letters in the alphabet:
- (a) M (13th letter) and S (19th letter): Difference = 6
- (b) B (2nd letter) and L (12th letter): Difference = 10
- (c) T (20th letter) and Y (25th letter): Difference = 5
- (d) F (6th letter) and J (10th letter): Difference = 4
Option (d) has a different letter-difference pattern compared to the others, making it the odd one out.
Q5: Directions : Find the missing number in each of the following figures.
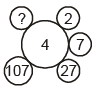
(a) 407
(b) 427
(c) 417
(d) 327
 View Answer
View Answer 
Ans: (b)
4 × 2 – 1 = 7
4 × 7 – 1 = 27
4 × 27 – 1 = 107
4 × 107 – 1 = 427
Q6: In the following series, what numbers should replace the question marks?
–1, 0, 1, 0, 2, 4, 1, 6, 9, 2, 12, 16, ? ? ?
(a) 11, 18, 27
(b) –1, 0, 3
(c) 3, 20, 25
(d) 4, 22, 29
 View Answer
View Answer 
Ans: (c)
This series contains three series in itself.
Term
T1 T2 T3 T4 T5 T6 T7 T8 T9 T10 T11 T12
–1 0 1 0 2 4 1 6 9 2 12 16
Series 1 (T1, T4, T7, T10): –1, 0, 1, 2 (AP with a common difference of +1)
Series 2 (T2, T5, T8, T11): 0, 2, 6, 12 (Differences between two terms increase by 2)
Series 3 (T3, T6, T9, T12): 1, 4, 9, 16 (Squares of consecutive numbers)
The next three numbers will thus be 3, 20 and 25.
Hence, option C.
Q7: Choose the appropriate sequence of mathematical signs from the options below to make the equation valid: 84 ◻ 21 ◻ 5 ◻ 10 ◻ 10
(a) ÷, –, ×, =
(b) =, ×, –, ÷
(c) ÷, ×, –, =
(d) ÷, =, ×, –
 View Answer
View Answer 
Ans: (c)
- To solve the equation, we need to find the right order of operations that makes the equation true.
- Using the signs ÷, ×, –, = in that order gives us: 84 ÷ 21 × 5 – 10 = 10.
- This simplifies to 4 × 5 – 10 = 10, which is correct since 20 – 10 equals 10.
- Thus, the correct sequence is ÷, ×, –, =, making option (c) the right choice.
Q8: If x > 8 and y > – 4, then which one of the following is always true?
(a) xy < 0
(b) x2 < – y
(c) – x < 2y
(d) x > y
 View Answer
View Answer 
Ans: (c)
Here x = 9, 10, 11 ....
y = – 3, – 2, – 1, 0, 1, 2, 3, ....
Q9: There is a specific connection between the two sets of terms on either side of the symbol : :. Determine the relationship of the first pair and find the missing term. JB : 20 : : EG : ?
(a) 35
(b) 30
(c) 25
(d) 40
 View Answer
View Answer 
Ans: (a)
- The first pair is JB and 20. The letters J and B are the 10th and 2nd letters of the alphabet, respectively. If you add these positions together (10 + 2), you get 12. However, the number given is 20.
- To find the relationship, we can see that 20 is actually 8 more than 12 (20 - 12 = 8).
- Now, looking at the second pair EG, the letters E and G are the 5th and 7th letters of the alphabet. Adding these gives us 12 (5 + 7 = 12).
- To find the missing term, we add 8 to 12 (12 + 8 = 20). Therefore, the missing term is 20.
Q10: Which letter in the word AMAZING is the same number in the word (counting from the beginning) as it is in the alphabet?
(a) N
(b) M
(c) I
(d) G
 View Answer
View Answer 
Ans: (d)
AMAZING- 7 letter is G, In English Alphabet 7 letter is G
Q11: A machine that arranges words and numbers follows a specific rule for rearranging them in each step. Below is an example of input and its rearrangement. Input: 41 take 12 proof 99 right 73 left
Step I: 99 41 take 12 proof right 73 left
Step II: 99 left 41 take 12 proof right 73
Step III: 99 left 73 41 take 12 proof right
Step IV: 99 left 73 proof 41 take 12 right
Step V: 99 left 73 proof 41 right take 12
Step VI: 99 left 73 proof 41 right 12 take
Step VI is the final step for the given input.
Based on the rule applied in the above steps, what will be the third step for the new input? Input: 83 sleep 24 good 49 night 16 now
(a) 83 good 49 night 24 sleep 16 now
(b) 83 good 49 night sleep 24 16 now
(c) 83 good 49 night 24 16 sleep now
(d) None of these
 View Answer
View Answer 
Ans: (b)
- The input consists of the words and numbers: 83, sleep, 24, good, 49, night, 16, now.
- In the rearrangement process, the first element is consistently moved to the front, followed by the next elements in a specific order.
- Following the same pattern as in the example, the third step will have the arrangement: 83 good 49 night sleep 24 16 now.
- This matches option (b), confirming it as the correct answer.
Q12: If one is added to the middle digit of each number and then the first and third digits of each of the given numbers are interchanged, then which of the following is the middle digit of the highest number thus formed?
(a) 6
(b) 8
(c) 7
(d) 9
 View Answer
View Answer 
Ans: (b)
- First, we take the numbers: 462, 373, 564, 879, 263, 147.
- Next, we add 1 to the middle digit of each number: 462 becomes 472, 373 becomes 383, 564 becomes 574, 879 becomes 889, 263 becomes 273, and 147 becomes 157.
- Then, we interchange the first and third digits: 472 becomes 274, 383 becomes 383, 574 becomes 475, 889 becomes 988, 273 becomes 372, and 157 becomes 751.
- Now, we find the highest number from these: 988 is the highest, and its middle digit is 8.
Directions (13-14): Each of the following questions consists of two sets of figures. Figures 1, 2, 3 and 4 constitute the problem set while figures (a), (b), (c) and (d) constitute the answer set. There is a definite relationship between figures (1) and (2) a similar relationship between figures (3) and (4) by selecting a suitable figure from the answer set that would replace the problem mark (?) in fig (4).
Q13: 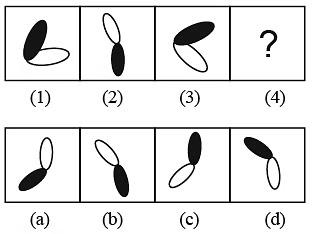 (a) a
(a) a
(b) b
(c) c
(d) d
 View Answer
View Answer 
Ans: (a)
Rotation of dark leaf is 135° (clock wise). Rotation of white leaf in 135° (anticlockwise). So for fig (3) option (a) is correct.
Q14: 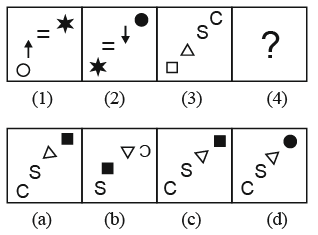 (a) a
(a) a
(b) b
(c) c
(d) d
 View Answer
View Answer 
Ans: (c)
Q15: Identify the missing number by applying a specific rule either across the rows or down the columns. (Table-Based Question)
(a) 76
(b) 70
(c) 78
(d) 74
 View Answer
View Answer 
Ans: (a)
- To find the missing number, we need to look for a pattern in the numbers provided in the table.
- By analyzing the rows or columns, we can determine how the numbers relate to each other.
- In this case, the correct answer is 76, which fits the established pattern.
- Understanding the rule applied in the table is crucial to identifying the missing number accurately.
Mathematical Reasoning
Q16: If sin²θ = cos²θ, then 2 tan²θ + sin²θ – 1 = ____.
(a) −3/2
(b) 3/2
(c) 2/3
(d) −2/3
 View Answer
View Answer 
Ans: (b)
- Given that sin²θ = cos²θ, we can use the identity sin²θ + cos²θ = 1 to find that sin²θ = 1/2 and cos²θ = 1/2.
- From this, we can calculate tan²θ = sin²θ/cos²θ = (1/2)/(1/2) = 1.
- Now, substituting tan²θ and sin²θ into the equation: 2(1) + (1/2) - 1 = 2 + 0.5 - 1 = 1.5 = 3/2.
- Thus, the final answer is 3/2.
Q17: If the zeroes of the rational expression (3x + 2a) (2x + 1) are -1/2 and b/3 then the value of a is:
(a) -2b
(b) -b/2
(c) -b/3
(d) None of these
 View Answer
View Answer 
Ans: (b)
As zero of 2x + 1 is -1/2 zero of the expression 3x+2a is b/3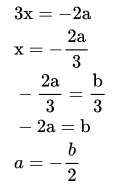
Q18: The first term of a series is 10, the last 45, and the sum 550; find the common difference.
(a) 37/19
(b) 35/19
(c) 53/19
(d) 35/17
 View Answer
View Answer 
Ans: (b)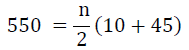 n = 20
n = 20
If d be the common difference 45 = the 20th term = 10 + 19d
d= 35/19
Q19: Which of the following represents the solutions to the equation 15/(x + 2) + (x - 1) / (x - 2) = 5; where x ≠ 2, -2?
(a) 1, 3
(b) 3/2, 4
(c) 2, 7
(d) 5, 4
 View Answer
View Answer 
Ans: (a)
- To find the roots of the equation, we first simplify it by eliminating the fractions. This involves multiplying through by the common denominator, which is (x + 2)(x - 2).
- After simplification, we rearrange the equation to form a standard polynomial equation.
- By solving this polynomial, we find the values of x that satisfy the equation, which are 1 and 3.
- Thus, the correct solutions are the roots 1 and 3, making option (a) the right choice.
Q20: If the mid-point of the line connecting (2, 5) and (3, k) is (x, y) and it also lies on the line 4x + 3y – 1 = 0, what is the value of k?
(a) 19
(b) −11
(c) 13
(d) −17
 View Answer
View Answer 
Ans: (b)
- To find the mid-point of the line segment joining the points (2, 5) and (3, k), we use the formula: Mid-point = ((x1 + x2)/2, (y1 + y2)/2).
- Substituting the values, we get Mid-point = ((2 + 3)/2, (5 + k)/2) = (2.5, (5 + k)/2).
- This mid-point (2.5, (5 + k)/2) must satisfy the line equation 4x + 3y - 1 = 0. Plugging in x = 2.5 gives us 4(2.5) + 3((5 + k)/2) - 1 = 0.
- Solving this equation leads to k = -11, which is the correct answer.
Q21: The length of a room is twice its breadth. The height of the room is 4 m. If the area of its four walls (including doors) is 144 m², what is the total surface area of the room?
(a) 342 m²
(b) 288 m²
(c) 358 m²
(d) 256 m²
 View Answer
View Answer 
Ans: (b)
- Let the breadth of the room be b meters. Then, the length is 2b meters.
- The height of the room is given as 4 m.
- The area of the four walls is calculated using the formula: 2 * height * (length + breadth).
- Substituting the values: 2 * 4 * (2b + b) = 144, which simplifies to 12b = 144, giving b = 12 m.
- Now, the length is 24 m (since length = 2 * breadth). The total surface area includes the floor and ceiling: 2 * (length * breadth + length * height + breadth * height).
- Calculating this gives: 2 * (24 * 12 + 24 * 4 + 12 * 4) = 288 m².
Q22: Find the value of m so that the quadratic equation mx (x − 7) + 49 = 0 has two equal roots.
(a) 0, 2
(b) 0, 4
(c) -2, 0
(d) -5, -2
 View Answer
View Answer 
Ans: (b)
Equation is m x (x − 7) + 49 = 0.
mx2 − 7mx + 49 = 0
On comparing it to quadratic equation ax2 + bx + c = 0
Here we find that a = m, b = − 7 m and c = 49
For the quadratic equation to have equal roots, its discriminant D = 0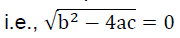 On substituting the values of a, b and c we get
On substituting the values of a, b and c we get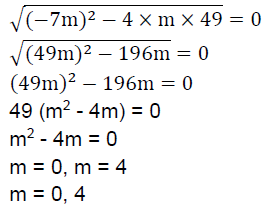
Q23: The probability of an event happening is P/2. If the probability of the event not happening is 5/8, what is the value of P?
(a) 5
(b) 3/4
(c) 8
(d) 9/2
 View Answer
View Answer 
Ans: (b)
- We know that the total probability of an event and its non-occurrence is always 1.
- Given that the probability of non-occurrence is 5/8, we can find the probability of occurrence: 1 - 5/8 = 3/8.
- We have the equation: P/2 = 3/8.
- To find P, we multiply both sides by 2: P = 3/8 * 2 = 3/4.
Q24: If the average of the five values x, x + 4, x + 8, x + 12, and x + 16 is 15, what is the value of x?
(a) 5
(b) 6
(c) 7
(d) 8
 View Answer
View Answer 
Ans: (c)
- To find the value of x, we first calculate the mean of the five observations.
- The sum of the observations is: x + (x + 4) + (x + 8) + (x + 12) + (x + 16) = 5x + 40.
- The mean is given by the formula: (sum of observations) / (number of observations). Here, it is (5x + 40) / 5 = 15.
- Multiplying both sides by 5 gives: 5x + 40 = 75. Solving for x, we get 5x = 35, so x = 7.
Q25: If the total of all zeros of the polynomial 5x² - (3 + k)x + 7 equals zero, what are the zeros of the polynomial 2x² - 2(k + 11)x + 30?
(a) 3, 5
(b) 7, 9
(c) 3, 6
(d) 2, 5
 View Answer
View Answer 
Ans: (a)
- To find the zeros of the polynomial, we first note that the sum of the zeros of the polynomial 5x² - (3 + k)x + 7 is given by the formula -b/a, which equals zero in this case.
- This implies that (3 + k) = 0, leading to k = -3.
- Substituting k into the second polynomial 2x² - 2(-3 + 11)x + 30 simplifies to 2x² - 16x + 30.
- Factoring or using the quadratic formula reveals that the zeros of this polynomial are 3 and 5.
Q26: If D is any point on the side BC of a ΔABC, then
(a) AB + BC + CA > 2AD
(b) AB + BC + CA < 2AD
(c) AB + BC + CA > 3AD
(d) None of these
 View Answer
View Answer 
Ans: (a)
If D is any point on the side BC of a ΔABC, then AB + BC + CA > 2 AD
Q27: Ron, Sam, Tom and Vera together had a total amount of $480 with them. Ron had half of the total amount with the others. Sam had one-third of the total amount with the others. Tom had one-fourth of the total amount with the others. Find the amount with Vera (in $).
(a) 128
(b) 140
(c) 104
(d) 116
 View Answer
View Answer 
Ans: (c)
Let r, s, t, v, be the amounts, with Ron, Sam, Tom, Vera respectively
The equations are: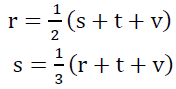
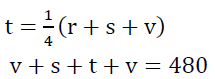 Now,
Now,
2r = (s + t + v)
2r = 480 - r
3r = 480
r = 160
Similarly, s = 120 and t = 96
r + s + t + v = 480
v = 104
Q28: (tan a + cosec b)2 − (cot b − sec a)2 is equivalent to?
(a) tan tan a cot cot b (sec b + cose a)
(b) tan tan a cot cot b (sec b − cose a)
(c) 2 tan tan a cot cot b (sec b + cos a)
(d) 2 tan tan a cot cot b (sec b − cose a)
 View Answer
View Answer 
Ans: (c)
(tan a + cosec b)2−(cot b − sec a)2
tan2a + cosec2b + 2tan tan a cosec b − cot2b− sec2a + 2cot cot b sec sec a
tan2a−sec2a + cosec2b − cot2b + 2(tan a cosec b+ cot b sec a)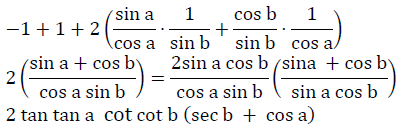
Q29: Determine the value of a – b, given that (√11 - √7) / (√11 + √7) = a - b√77
(a) 16
(b) 4
(c) 12
(d) 8
 View Answer
View Answer 
Ans: (b)
- To solve for a and b, we start with the expression (√11 - √7) / (√11 + √7).
- By rationalizing the denominator, we multiply the numerator and denominator by (√11 - √7).
- This gives us (11 - 7) / ((√11 + √7)(√11 - √7)) = 4 / (11 - 7) = 4 / 4 = 1.
- Thus, we can express this as 1 = a - b√77, leading us to find that a = 4 and b = 1.
Q30: In a fraction, if 1 is added to the denominator, the fraction becomes 2/3. Additionally, if 5 is added to the numerator, the fraction becomes 1. What is the value of the numerator of the original fraction?
(a) 12
(b) 13
(c) 17
(d) 19
 View Answer
View Answer 
Ans: (a)
- Let the original fraction be x/y.
- According to the first condition, (x)/(y+1) = 2/3, which can be rearranged to 3x = 2(y + 1).
- From the second condition, (x + 5)/y = 1, leading to x + 5 = y.
- Substituting y = x + 5 into the first equation gives 3x = 2((x + 5) + 1), which simplifies to 3x = 2x + 12.
- Solving this, we find x = 12, which is the numerator of the original fraction.
Q31: Find the points of trisection of the line formed by joining (1, -3) and (-3, 5).
(a) 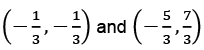 (b)
(b) 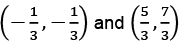 (c)
(c) 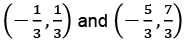 (d)
(d) 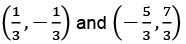
 View Answer
View Answer 
Ans: (a)
Let the points (1, -3) and (-3, 5) be A and B respectively.
If P and Q be the points of trisection of AB, the ratio AP: PB will be equal to 1:2 and the ratio AQ: QB will be equal to 2:1.
Hence the coordinates of P are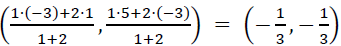 And Co-ordinates of Q are
And Co-ordinates of Q are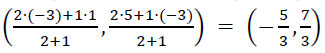
Q32: The first term of an A.P. is 21. If the sum of its first 6 terms is half of the sum of its next 6 terms, then find the common difference of the A.P.
(a) 4
(b) 6
(c) 5
(d) 3
 View Answer
View Answer 
Ans: (b)
- In an Arithmetic Progression (A.P.), the sum of the first n terms can be calculated using the formula: S_n = n/2 * (2a + (n - 1)d), where a is the first term and d is the common difference.
- Here, the first term a = 21 and we need to find the common difference d.
- The sum of the first 6 terms is S_6 = 6/2 * (2*21 + 5d) = 3(42 + 5d).
- The sum of the next 6 terms (7th to 12th) is S_6 = 6/2 * (2*(21 + 6d) + 5d) = 3(42 + 11d).
- According to the problem, S_6 (first 6 terms) = 1/2 * S_6 (next 6 terms), leading to the equation: 3(42 + 5d) = 1/2 * 3(42 + 11d).
- Solving this gives d = 6.
Q33: A triangle and a parallelogram have the same base and the same area. If the sides of the triangle are 9 cm, 12 cm, and 15 cm and the parallelogram stands on the base 12 cm, then find the height of the parallelogram.
(a) 14 cm
(b) 6.5 cm
(c) 8 cm
(d) 4.5 cm
 View Answer
View Answer 
Ans: (d)
- To find the height of the parallelogram, we first need to calculate the area of the triangle using Heron's formula.
- The semi-perimeter (s) of the triangle is calculated as (9 + 12 + 15) / 2 = 18 cm.
- Using Heron's formula, the area of the triangle is √[s(s-a)(s-b)(s-c)] = √[18(18-9)(18-12)(18-15)] = √[18 * 9 * 6 * 3] = 54 cm².
- Since the area of the parallelogram is the same, we can use the formula Area = base × height. Here, Area = 54 cm² and base = 12 cm.
- Thus, height = Area / base = 54 cm² / 12 cm = 4.5 cm.
Q34: If p = sec θ − tan θ and q = cosec θ + cot θ, find pq + 1.
(a) p + q
(b) − (p + q)
(c) − 1
(d) q − p
 View Answer
View Answer 
Ans: (d)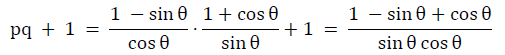
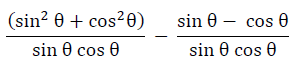 =(tan θ + cot θ)−(sec θ − cosec θ)
=(tan θ + cot θ)−(sec θ − cosec θ)
(cosec θ+cot θ)−(sec θ −tan θ) = q −p
Q35: If the HCF of 135 and 216 is represented as 87x – 147, what is the value of x?
(a) 5
(b) 3
(c) 2
(d) 6
 View Answer
View Answer 
Ans: (c)
- To find the value of x, we first need to determine the HCF (Highest Common Factor) of 135 and 216, which is 27.
- Next, we set up the equation: 87x - 147 = 27.
- By rearranging, we get 87x = 27 + 147, which simplifies to 87x = 174.
- Dividing both sides by 87, we find x = 2.
Everyday Mathematics
Q36: Four different electronic devices emit a beep after intervals of 30 minutes, 1 hour, 1.5 hours, and 1 hour 45 minutes respectively. All devices beeped simultaneously at 12 noon. When will they beep together again?
(a) 12 midnight
(b) 3 a.m.
(c) 6 a.m.
(d) 9 a.m.
 View Answer
View Answer 
Ans: (d)
- The devices beep at different intervals: 30 minutes, 1 hour, 1.5 hours, and 1 hour 45 minutes.
- To find when they beep together again, we need to calculate the Least Common Multiple (LCM) of these intervals.
- The LCM of 30, 60, 90, and 105 minutes is 540 minutes, which equals 9 hours.
- Starting from 12 noon, adding 9 hours brings us to 9 p.m..
Q37: The perimeter of a triangular field is 168 m. If two of its sides are 60 m and 52 m, then find the cost of watering the field at ₹ 5 per m2.
(a) ₹ 5275
(b) ₹ 4850
(c) ₹ 3260
(d) ₹ 6720
 View Answer
View Answer 
Ans: (d)
- To find the third side of the triangle, we subtract the sum of the two known sides from the perimeter: 168 m - (60 m + 52 m) = 56 m.
- Next, we calculate the area of the triangle using Heron's formula. The semi-perimeter (s) is (168 m / 2) = 84 m.
- Using Heron's formula: Area = √[s(s-a)(s-b)(s-c)], where a, b, and c are the sides of the triangle. Plugging in the values gives us the area.
- Finally, to find the cost of watering, we multiply the area by ₹ 5 per m2. The total cost comes out to be ₹ 6720.
Q38: A tank can be filled by two taps A and B in 12 hours and 15 hours respectively. The full tank can be emptied by tap C in 8 hours. If all the taps are opened at the same time, then in how much time will the empty tank be filled completely?
(a) 120/13 hours
(b) 120/7 hours
(c) 144/3 hours
(d) None of these
 View Answer
View Answer 
Ans: (d)
- To find out how long it takes to fill the tank with all taps open, we first calculate the rates of each tap:
- Tap A fills the tank at a rate of 1/12 tanks per hour.
- Tap B fills the tank at a rate of 1/15 tanks per hour.
- Tap C empties the tank at a rate of 1/8 tanks per hour.
- When all taps are open, the combined rate is (1/12 + 1/15 - 1/8) tanks per hour.
- Finding a common denominator (120), we get: (10/120 + 8/120 - 15/120) = 3/120 = 1/40 tanks per hour.
- This means it will take 40 hours to fill the tank completely when all taps are open.
- Since 40 hours is not listed in the options, the correct answer is None of these.
Q39: The current age of Saurav is 6 years younger than twice the age of his daughter. If x denotes Saurav's current age and y denotes his daughter's current age, which equation correctly represents this scenario?
(a) 2x – 6y = 0
(b) 2x – y = 6
(c) x – 2y = 6
(d) 2y – x = 6
 View Answer
View Answer 
Ans: (d)
- We know that Saurav's age is 6 years less than twice his daughter's age.
- This can be expressed as: x = 2y - 6.
- Rearranging this gives us: 2y - x = 6, which matches option (d).
- Thus, option (d) correctly represents the relationship between their ages.
Q40: ₹ 6500 was shared equally among a specific number of individuals. If there had been 15 additional individuals, each person would have received ₹ 30 less. Determine the original number of individuals.
(a) 50
(b) 60
(c) 45
(d) 55
 View Answer
View Answer 
Ans: (a)
- Let the original number of persons be x.
- Each person initially receives ₹ 6500/x.
- With 15 more persons, the number becomes x + 15, and each would then receive ₹ 6500/(x + 15).
- According to the problem, the difference in amount received is ₹ 30, leading to the equation: ₹ 6500/x - ₹ 6500/(x + 15) = ₹ 30.
- Solving this equation gives x = 50, which is the original number of persons.
Q41: A box contains 50 bolts and 150 nuts. Upon inspection, it was discovered that half of the bolts and half of the nuts are rusted. If one item is selected at random, what is the probability that it is rusted?
(a) 1/4
(b) 1/2
(c) 1/5
(d) 1/10
 View Answer
View Answer 
Ans: (b)
- There are a total of 200 items in the box (50 bolts + 150 nuts).
- Half of the bolts are rusted, which means 25 bolts are rusted.
- Half of the nuts are rusted, resulting in 75 rusted nuts.
- So, the total number of rusted items is 25 + 75 = 100.
- The probability of picking a rusted item is 100 rusted items out of 200 total items, which simplifies to 1/2.
Q42: The base radius of the cylinder is 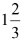 times its height. The cost of painting its curved surface area at 2 paise/cm2 is ₹ 92.40. What is the volume of the cylinder?
times its height. The cost of painting its curved surface area at 2 paise/cm2 is ₹ 92.40. What is the volume of the cylinder?
(a) 80850 cm3
(b) 88850 cm3
(c) 80508 cm3
(d) 90000 cm3
Ans: (a)
- The curved surface area (CSA) of a cylinder is calculated using the formula: CSA = 2πrh, where r is the radius and h is the height.
- Given that the base radius is
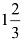 times the height, we can express r as (5/3)h.
times the height, we can express r as (5/3)h. - The cost of painting the CSA is ₹ 92.40, which translates to 9240 paise. Since the cost is 2 paise/cm2, the total CSA is 9240 / 2 = 4620 cm².
- By substituting the values into the CSA formula and solving for h, we can find the volume using the formula: Volume = πr2h.
- After calculations, the volume of the cylinder is determined to be 80850 cm³.
Q43: The pocket money of 24 students of a class is arranged in an A.P. The lowest pocket money of a student is ₹ 250. If the difference between two consecutive amounts of pocket money is ₹ 15, then find the total pocket money of all the students.
(a) ₹ 15250
(b) ₹ 10140
(c) ₹ 21200
(d) ₹ 18430
 View Answer
View Answer 
Ans: (b)
- In an Arithmetic Progression (A.P), the total can be calculated using the formula: Total = n/2 * (2a + (n-1)d), where n is the number of terms, a is the first term, and d is the common difference.
- Here, n = 24, a = 250, and d = 15.
- Plugging in the values: Total = 24/2 * (2*250 + (24-1)*15).
- This simplifies to Total = 12 * (500 + 345) = 12 * 845 = ₹ 10140.
Q44: Find the length of side BC, if PQ || CA. The unit used for measurement is cm.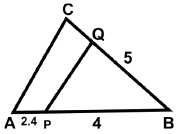 (a) 8 cm
(a) 8 cm
(b) 4 cm
(c) 6 cm
(d) 4.8 cm
 View Answer
View Answer 
Ans: (a)
AB = (2.4 + 4) cm = 6.4 cm.
BQ/BC = BP/AB
BC = (6.4 × 5) ÷ 4 = 8 cm
Q45: Three men and five girls can complete a task in six days. If two men and seven girls can finish it in five days, how long will it take for sixteen men and twenty girls to finish the same task?
(a) 1 3/25 days
(b) 1 1/8 days
(c) 1 3/8 days
(d) 2 8/25 days
 View Answer
View Answer 
Ans: (c)
- To solve this, we first determine the work done by men and girls in terms of work units per day.
- From the first scenario, 3 men and 5 girls complete the work in 6 days, which means they do 1/6 of the work per day.
- From the second scenario, 2 men and 7 girls finish the work in 5 days, equating to 1/5 of the work per day.
- By calculating the work rates of men and girls, we can find the combined rate for 16 men and 20 girls.
- Finally, we find that 16 men and 20 girls can complete the work in 1 3/8 days.
Achievers Section
Q46: Read the following statements carefully and select the correct option. Statement I: If 2 is a root of the equation x2 + kx + 12 = 0 and the equation x2 + kx + q = 0 has equal roots, then the value of q is 15. Statement II: The roots of the equation x2 - √2x + 1 = 0 are real and equal.
(a) Statement I is true but Statement II is false.
(b) Statement I is false but Statement II is true.
(c) Both Statement I and Statement II are true.
(d) Both Statement I and Statement II are false.
 View Answer
View Answer 
Ans: (d)
- Statement I is false because if 2 is a root of the equation, we can find k using the equation. However, for the second equation to have equal roots, q must be equal to k2/4, which does not equal 15.
- Statement II is also false because the roots of the equation x2 - √2x + 1 = 0 can be calculated using the discriminant. The discriminant is negative, indicating that the roots are not real and equal.
- Thus, both statements are incorrect, leading to the conclusion that the correct answer is (d).
Q47: A pendulum swings through an angle of 30º and describes an arc 22 cm in length. Find the length of the pendulum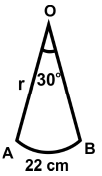 (a) 22 cm
(a) 22 cm
(b) 21 cm
(c) 42 cm
(d) 16 cm
 View Answer
View Answer 
Ans: (c)
Here θ= 30º, arc length = l = 22, length of the pendulum = radius = r
Q48: Fill in the blanks and select the correct option:
(i) A number is chosen randomly from the set of numbers 3, 4, 5, 7, 8, 7, 9, 4, 9, 2. The probability that the chosen number is an odd number is P.
(ii) When rolling a die, the probability of rolling an even prime number is Q.
(iii) If P(E) = 0.74, then P(not E) is R.
(a) P = 1/5, Q = 2/3, R = 74/100
(b) P = 3/10, Q = 1/6, R = 13/25
(c) P = 7/10, Q = 1/3, R = 27/100
(d) P = 3/5, Q = 1/6, R = 13/50
 View Answer
View Answer 
Ans: (d)
- To find P: The odd numbers in the set are 3, 5, 7, 7, and 9. There are 5 odd numbers out of 10 total numbers, so P = 5/10 = 1/2.
- To find Q: The only even prime number is 2. When rolling a die, there are 6 outcomes, so Q = 1/6.
- To find R: P(not E) = 1 - P(E) = 1 - 0.74 = 0.26, which is 26/100.
- Thus, the correct values are P = 3/5, Q = 1/6, R = 13/50, making option (d) the right choice.
Q49: Select the incorrect option.
(a) The HCF and LCM of two numbers are 27 and 162 respectively. If one of the numbers is 54, then the other number is 81.
(b) The LCM of the smallest prime number and the smallest composite number is 4.
(c) 3√2 is an irrational number.
(d) None of these
 View Answer
View Answer 
Ans: (d)
- The statement in option (a) is correct because the HCF (Highest Common Factor) and LCM (Lowest Common Multiple) relationship holds true for the numbers given.
- In option (b), the smallest prime number is 2 and the smallest composite number is 4; their LCM is indeed 4.
- Option (c) is also correct since 3√2 cannot be expressed as a fraction, making it an irrational number.
- Therefore, option (d) is the correct answer as it states that none of the previous options are incorrect.
Q50: Read the given statements carefully and state 'T' for true and 'F' for false:
(i) If A is a point on the x-axis whose abscissa is 8 and the coordinates of point B are (–4, 9), then the distance AB is 15 units.
(ii) The x-axis divides the line joining the points (–3, –5) and (7, 4) in the ratio of 7:3.
(iii) The points (7, –14), (–3, 4), and (2, –5) are collinear.
(a) T, T, F
(b) F, T, F
(c) F, T, T
(d) T, F, T
 View Answer
View Answer 
Ans: (d)
- Statement (i): To find the distance AB, we use the distance formula. The distance between A(8, 0) and B(–4, 9) is calculated as √[(8 - (–4))² + (0 - 9)²] = √[(12)² + (–9)²] = √[144 + 81] = √225 = 15 units, which is true.
- Statement (ii): The x-axis divides the line segment joining (–3, –5) and (7, 4) in the ratio of 7:3, which is false. The actual ratio is different.
- Statement (iii): To check if the points (7, –14), (–3, 4), and (2, –5) are collinear, we can use the area method or slope method. They do not lie on the same straight line, making this statement false.
Thus, the correct answers are T, F, T, leading to the answer (d).
|
70 videos|242 docs|187 tests
|
FAQs on Mathematics Olympiad Model Test Papers - 1 - Olympiad Preparation for Class 10
| 1. What topics are covered in the Class 10 Mathematics Olympiad Model Test Papers? |  |
| 2. How can I effectively prepare for the Class 10 Mathematics Olympiad? |  |
| 3. Are there any specific strategies for solving Logical Reasoning questions in the Olympiad? |  |
| 4. What is the importance of Everyday Mathematics in the Olympiad? |  |
| 5. How can students assess their performance after attempting the model test papers? |  |




















